Memoisasi (1D, 2D dan 3D) Pengaturcaraan Dinamik di Jawa

Memoisasi ialah teknik berdasarkan pengaturcaraan dinamik yang digunakan untuk meningkatkan prestasi algoritma rekursif dengan memastikan kaedah tidak berjalan beberapa kali pada set input yang sama, dengan merekodkan keputusan (disimpan dalam tatasusunan) input yang disediakan. Memoisasi boleh dicapai melalui pendekatan atas ke bawah yang melaksanakan kaedah rekursif.

Mari kita fahami situasi ini melalui contoh jujukan asas Fibonacci.

Memoisasi 1-D

Kami akan mempertimbangkan algoritma rekursif dengan hanya satu parameter bukan malar (hanya satu perubahan nilai parameter), jadi kaedah ini dipanggil memoisasi 1-D. Kod berikut adalah untuk mencari Nth (semua sebutan sehingga N) dalam jujukan Fibonacci.

Contoh

public int fibonacci(int n) {
   if (n == 0)
      return 0;
   if (n == 1)
      return 1;
   System.out.println("Calculating fibonacci number for: " + n);
   return (fibonacci(n - 1) + fibonacci(n - 2));
}

Output

Jika kita menjalankan kod di atas dengan n=5, output berikut akan dijana. Nilai Fibonacci untuk

Calculating fibonacci number for: 5
Calculating fibonacci number for: 4
Calculating fibonacci number for: 3
Calculating fibonacci number for: 2
Calculating fibonacci number for: 2
Calculating fibonacci number for: 3
Calculating fibonacci number for: 2

n=5 ialah: 5

Perhatikan bahawa nombor Fibonacci untuk 2 dan 3 dikira berbilang kali. Marilah kita memahami dengan lebih baik dengan melukis pepohon rekursi di atas untuk keadaan n=5.

Dua anak nod akan mewakili panggilan rekursif yang dibuatnya. Anda boleh melihat bahawa F(3) dan F(2) dikira berbilang kali, yang boleh dielakkan dengan menyimpan cache hasil selepas setiap langkah.

Kami akan menggunakan pembolehubah contoh Tetapkan memoize untuk cache keputusan. Mula-mula semak sama ada n sudah wujud dalam Set memoize, jika ya, kembalikan nilai jika tidak, hitung nilai dan tambahkannya pada set.

Contoh

import java.util.HashMap;
import java.util.Map;
public class TutorialPoint {
   private Map<Integer, Integer> memoizeSet = new HashMap<>(); // O(1)
   public int fibMemoize(int input) {
      if (input == 0)
         return 0;
      if (input == 1)
         return 1;
      if (this.memoizeSet.containsKey(input)) {
         System.out.println("Getting value from computed result for " + input);
         return this.memoizeSet.get(input);
      }
      int result = fibMemoize(input - 1) + fibMemoize(input - 2);
      System.out.println("Putting result in cache for " + input);
      this.memoizeSet.put(input, result);
      return result;
   }
   public int fibonacci(int n) {
      if (n == 0)
         return 0;
      if (n == 1)
         return 1;
      System.out.println("Calculating fibonacci number for: " + n);
      return (fibonacci(n - 1) + fibonacci(n - 2));
   }
   public static void main(String[] args) {
      TutorialPoint tutorialPoint = new TutorialPoint();
      System.out.println("Fibonacci value for n=5: " + tutorialPoint.fibMemoize(5));
   }
}

Output

Jika kita menjalankan kod di atas, output berikut akan dijana

Adding result in memoizeSet for 2
Adding result in memoizeSet for 3
Getting value from computed result for 2
Adding result in memoizeSet for 4
Getting value from computed result for 3
Adding result in memoizeSet for 5

Nilai Fibonacci untuk n=5 ialah: 5

Seperti yang anda lihat dari atas, nilai Fibonacci ​​2 dan 3 Nombor surat ikatan tidak akan dikira lagi. Di sini, kami memperkenalkan HashMap menghafal untuk menyimpan nilai yang dikira Sebelum setiap pengiraan Fibonacci, semak sama ada nilai input telah dikira dalam koleksi Jika tidak, tambah nilai input tertentu.

Hafazan 2-D

Dalam program di atas, kita hanya mempunyai satu parameter bukan tetap. Dalam atur cara berikut, kami akan mengambil contoh atur cara rekursif yang mempunyai dua parameter yang mengubah nilainya selepas setiap panggilan rekursif dan kami akan melaksanakan penghafalan pada dua parameter bukan malar untuk pengoptimuman. Ini dipanggil penghafalan 2-D.

Sebagai contoh: kami akan melaksanakan Urutan Sepunya Terpanjang yang standard (LCS). Jika satu set jujukan diberikan, masalah jujukan sepunya terpanjang ialah mencari jujukan sepunya kepada semua jujukan yang mempunyai panjang terbesar. Akan ada 2^n kombinasi yang mungkin.

Contoh

class TP {
   static int computeMax(int a, int b) {
      return (a > b) ? a : b;
   }
   static int longestComSs(String X, String Y, int m, int n) {
      if (m == 0 || n == 0)
         return 0;
      if (X.charAt(m - 1) == Y.charAt(n - 1))
         return 1 + longestComSs(X, Y, m - 1, n - 1);
      else
         return computeMax(longestComSs(X, Y, m, n - 1), longestComSs(X, Y, m - 1, n));
   }
   public static void main(String[] args) {
      String word_1 = "AGGTAB";
      String word_2 = "GXTXAYB";
      System.out.print("Length of LCS is " + longestComSs(word_1, word_2, word_1.length(),word_2.length()));
   }
}

Output

Jika kita menjalankan kod di atas, output berikut akan dijana

Length of LCS is 4

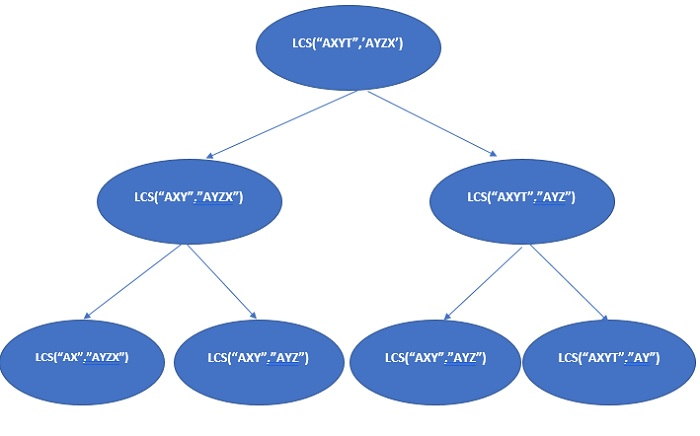
Dalam pepohon rekursi di atas, lcs("AXY", "AYZ") diselesaikan beberapa kali.

Disebabkan sifat masalah ini dengan substruktur yang bertindih, pengiraan berulang bagi submasalah yang sama boleh dielakkan dengan menggunakan memoisasi atau penjadualan.

Kaedah memoisasi kod rekursif dilaksanakan seperti berikut.

Contoh

import java.io.*;
import java.lang.*;
class testClass {
   final static int maxSize = 1000;
   public static int arr[][] = new int[maxSize][maxSize];
   public static int calculatelcs(String str_1, String str_2, int m, int n) {
      if (m == 0 || n == 0)
         return 0;
      if (arr[m - 1][n - 1] != -1)
         return arr[m - 1][n - 1];
      if (str_1.charAt(m - 1) == str_2.charAt(n - 1)) {
         arr[m - 1][n - 1] = 1 + calculatelcs(str_1, str_2, m - 1, n - 1);
         return arr[m - 1][n - 1];
      }
      else {
         int a = calculatelcs(str_1, str_2, m, n - 1);
         int b = calculatelcs(str_1, str_2, m - 1, n);
         int max = (a > b) ? a : b;
         arr[m - 1][n - 1] = max;
         return arr[m - 1][n - 1];
      }
   }
   public static void main(String[] args) {
      for (int i = 0; i < 1000; i++) {
         for (int j = 0; j < 1000; j++) {
            arr[i][j] = -1;
         }
      }
      String str_1 = "AGGTAB";
      String str_2 = "GXTXAYB";
      System.out.println("Length of LCS is " + calculatelcs(str_1, str_2, str_1.length(),str_2.length()));
   }
}

Output

Jika kita menjalankan kod di atas, output berikut akan dijana

Length of LCS is 4

Kaedah

Diperhatikan bahawa terdapat 4 parameter dalam kaedah (calculatelcs), yang mana tidak terdapat 2 pemalar mempengaruhi penghafalan), dan terdapat 2 parameter bukan malar (m dan n), yang nilainya akan berubah setiap kali kaedah dipanggil secara rekursif. Untuk mencapai hafalan, kami memperkenalkan tatasusunan dua dimensi untuk menyimpan nilai terkira lcs(m,n), yang disimpan dalam arr[m-1][n-1]. Apabila memanggil fungsi dengan parameter yang sama m dan n sekali lagi, kami tidak lagi melakukan panggilan rekursif, tetapi terus mengembalikan arr[m-1][n-1], kerana lcs(m, n) yang dikira sebelum ini telah disimpan dalam arr [m-1][n-1], dengan itu mengurangkan bilangan panggilan rekursif.

Memoisasi tiga dimensi

Ini ialah kaedah menghafal untuk program rekursif dengan 3 parameter bukan tetap. Di sini, kami mengambil pengiraan panjang LCS bagi tiga rentetan sebagai contoh.

Pendekatan di sini adalah untuk menjana semua kemungkinan susulan bagi rentetan tertentu (terdapat 3ⁿ kemungkinan susulan kesemuanya) dan memadankan urutan sepunya terpanjang di antaranya.

Kami akan memperkenalkan jadual tiga dimensi untuk menyimpan nilai yang dikira. Pertimbangkan susulan.

• A1[1...i] i < N

• A2[1...j] j <

Jika kita menemui aksara biasa (X[i]==Y[j]==Z[k]), kita perlu memproses aksara yang tinggal secara rekursif. Jika tidak, kami akan mengira maksimum kes berikut
Simpan

Jadi, jika kita menukar idea di atas kepada fungsi rekursif, maka

• f(N,M,K)={1+f(N -1,M-1,K-1)jika (X[N] ==Y[M]==Z[K]maksimum(f(N-1,M,K),f(N,M-1, K),f(N,M,K-1))}

• f(N-1,M,K) = Simpan X[i] untuk memproses aksara lain secara rekursif

• f(N,M- 1,K) = Simpan Y[j] untuk memproses aksara lain secara rekursif

f(N,M,K-1) = Simpan Z[k] Memproses aksara lain secara rekursif

Contoh

import java.io.IOException;
import java.io.InputStream;
import java.util.*;
class testClass {
   public static int[][][] arr = new int[100][100][100];
   static int calculatelcs(String str_1, String str_2, String str_3, int m, int n, int o) {
         for (int i = 0; i <= m; i++) {
            for (int j = 0; j <= n; j++) {
               arr[i][j][0] = 0;
            }
         }
         for (int i = 0; i <= n; i++) {
            for (int j = 0; j <= o; j++) {
               arr[0][i][j] = 0;
            }
         }
         for (int i = 0; i <= m; i++) {
            for (int j = 0; j <= o; j++) {
               arr[i][0][j] = 0;
            }
         }
         for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
               for (int k = 1; k <= o; k++) {
                  if (str_1.charAt(i - 1) == str_2.charAt(j-1) && str_2.charAt(j1) == str_3.charAt(k-1)) {
                     arr[i][j][k] = 1 + arr[i - 1][j - 1][k - 1];
                  }
                  else {
                     arr[i][j][k] = calculateMax(arr[i - 1][j][k], arr[i][j - 1][k], arr[i][j][k - 1]);
                  }
               }
            }
         }
         return arr[m][n][o];
   }
   static int calculateMax(int a, int b, int c) {
      if (a > b && a > c)
         return a;
         if (b > c)
         return b;
         return c;
   }
   public static void main(String[] args) {
      String str_1 = "clued";
      String str_2 = "clueless";
      String str_3 = "xcxclueing";
      int m = str_1.length();
      int n = str_2.length();
      int o = str_3.length();
      System.out.print("Length of LCS is " + calculatelcs(str_1, str_2, str_3, m, n, o));
   }
}

• Output

  Jika kita menjalankan kod di atas, output berikut akan dihasilkan

  Length of LCS is 4

  Atas ialah kandungan terperinci Memoisasi (1D, 2D dan 3D) Pengaturcaraan Dinamik di Jawa. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!