 pembangunan bahagian belakang
pembangunan bahagian belakang
 C++
C++
 Jumlah maksimum tatasusunan yang mungkin selepas melakukan operasi yang diberikan
Jumlah maksimum tatasusunan yang mungkin selepas melakukan operasi yang diberikan
Jumlah maksimum tatasusunan yang mungkin selepas melakukan operasi yang diberikan

Dalam soalan ini, kami akan melaksanakan operasi yang diberikan pada elemen tatasusunan dan mencari jumlah maksimum akhir.
Di sini, dalam setiap operasi, kita boleh memilih paling banyak elemen X[p] daripada tatasusunan dan menggantikannya dengan elemen Y[p] untuk memaksimumkan jumlah.
Dalam kaedah mudah kita akan mencari elemen tatasusunan X[p] yang lebih kecil daripada elemen Y[p] dan menggantikannya dengan Y[p].
Dalam pendekatan yang cekap kami akan menggunakan baris gilir keutamaan untuk mendapatkan jumlah maksimum.
Pernyataan Masalah− Kami diberi tatasusunan nums[] yang mengandungi N nombor. Pada masa yang sama, kita diberikan tatasusunan X[] dan Y[] yang mengandungi integer M. Kita perlu melakukan operasi berikut pada tatasusunan nums[].
Kita perlu melakukan operasi M pada setiap elemen X[] dan Y[]. Dalam setiap operasi, kita perlu memilih elemen X[p] terbesar daripada nombor tatasusunan[] dan menggantikannya dengan Y[p].
Tugas yang diberikan ialah mencari jumlah maksimum unsur tatasusunan nums[] selepas melakukan operasi M.
Contoh Contoh
Masuk
nums[] = {10, 8, 7, 60, 20, 18, 30, 60}; m = 3; x[] = {1, 2, 5}; y[] = {500, 10, 2};
Output
708
Penjelasan − Mari lakukan setiap operasi satu persatu.
Dalam operasi pertama, kami akan menggantikan 7 elemen dengan 500. Jadi, tatasusunan menjadi {10, 8, 500, 60, 20, 18, 30, 60}.
Dalam operasi kedua, kita boleh menggantikan sehingga 2 elemen dengan 10, tetapi kita hanya mempunyai 1 elemen kurang daripada 10. Jadi, kita gantikan 8 dengan 10 dan tatasusunan menjadi {10, 10, 500, 60, 20, 18, 30, 60}.
Dalam operasi ketiga, kita boleh menggantikan sehingga 5 elemen dengan 2, tetapi tiada unsur kurang daripada 2 dalam tatasusunan. Oleh itu, kami tidak akan menggantikan mana-mana elemen.
Masuk
nums[] = {30, 40, 50, 50, 60}; m = 3; x[] = {2, 3, 6}; y[] = {10, 8, 21};
Output
230
Penjelasan − Semua elemen tatasusunan y[] adalah lebih kecil daripada unsur tatasusunan asal. Oleh itu, kita tidak perlu menggantikan mana-mana elemen tatasusunan yang diberikan untuk mendapatkan jumlah maksimum.
Masuk
nums[] = {30, 40, 50, 50, 60}; m = 3; x[] = {2, 4, 5}; y[] = {50, 60, 100};
Output
500
Penjelasan − Di sini, kita boleh menggantikan sehingga x[p] elemen dalam setiap operasi. Dalam operasi terakhir, kita boleh menggantikan setiap elemen dalam tatasusunan dengan 100, menghasilkan jumlah maksimum yang sama dengan 100.
Kaedah 1
Dalam kaedah ini, kami akan mengulangi tatasusunan x[] dan y[]. Dalam setiap lelaran, kami akan mengisih tatasusunan untuk mendapatkan paling banyak unsur tatasusunan x[p] yang lebih kecil daripada elemen y[p] dan menggantikannya dengan y[p].
Algoritma
Langkah 1 − Mulakan 'maxSum' kepada 0, yang digunakan untuk menyimpan jumlah maksimum elemen tatasusunan.
Langkah 2 − Mula melintasi elemen tatasusunan x[] dan y[].
Langkah 3 − Simpan nilai x[p] ke dalam pembolehubah sementara dan susun tatasusunan nums[].
Langkah 4− Mula melintasi tatasusunan yang diisih dalam gelung.
Langkah 5 − Jika suhu lebih besar daripada 0 dan nums[q] kurang daripada y[p], kemas kini nombor[q] dengan y[p] dan kurangkan nilai temp sebanyak 1.
Langkah 6− Di luar gelung, mula merentasi tatasusunan yang dikemas kini, keluarkan jumlah semua elemen tatasusunan dan simpannya dalam pembolehubah maxSum.
Langkah 7 − Kembalikan maxSum pada penghujung fungsi.
Contoh
#include <bits/stdc++.h>
using namespace std;
int getMaxSum(int nums[], int n, int q, int x[], int y[]) {
int maxSum = 0;
// Traverse X[] and Y[] array
for (int p = 0; p < q; p++) {
// Replacing x[p] number of elements of nums[] array with y[p] if they are lesser than y[p]
int temp = x[p];
sort(nums, nums + n);
for (int q = 0; q < n; q++) {
if (temp > 0 && nums[q] < y[p]) {
nums[q] = y[p];
temp--;
}
}
}
// Sum of the array
for (int p = 0; p < n; p++) {
maxSum += nums[p];
}
return maxSum;
}
int main() {
int nums[] = {10, 8, 7, 60, 20, 18, 30, 60};
int n = (sizeof nums) / (sizeof nums[0]);
int m = 3;
int x[] = {1, 2, 5};
int y[] = {500, 10, 2};
cout << "The maximum sum we can get by replacing the array values is " << getMaxSum(nums, n, m, x, y);
return 0;
}
Output
The maximum sum we can get by replacing the array values is 708
Kerumitan masa− O(M*NlogN), di mana O(M) digunakan untuk merentasi semua pertanyaan dan O(NlogN) digunakan untuk mengisih tatasusunan.
Kerumitan Angkasa− Untuk mengisih tatasusunan, kerumitan ruang ialah O(N).
Kaedah 2
Dalam kaedah ini, kami akan menggunakan baris gilir keutamaan untuk menyimpan pasangan elemen tatasusunan dan kiraan kejadiannya.
Sebagai contoh, kami akan menolak pasangan {nums[p],1} ke dalam baris gilir keutamaan untuk setiap elemen tatasusunan. Pada masa yang sama, kami menolak pasangan {y[p], x[p]} ke dalam baris gilir keutamaan. Dalam baris gilir keutamaan, pasangan akan diisih berdasarkan elemen pertama. Oleh itu, kita boleh mengambil elemen N teratas daripada baris gilir. Di sini, untuk pasangan {y[p],x[p]}, kita boleh mengeluarkan unsur y[p] x[p] kali, dan kita perlu mengeluarkan sejumlah N elemen untuk memaksimumkan jumlahnya.
Algoritma
Langkah 1 − Mulakan 'maxSum' dengan 0 dan baris gilir keutamaan untuk menyimpan pasangan elemen dan bilangan kejadiannya.
Langkah 2− Untuk semua elemen tatasusunan, masukkan {nums[p], 1} pasangan ke dalam baris gilir.
Langkah 3 − Kemudian, masukkan pasangan {y[p], x[p]} ke dalam baris gilir keutamaan.
Langkah 4− Ulang sehingga n lebih besar daripada 0.
Langkah 4.1 − Alih keluar elemen pertama daripada baris gilir keutamaan.
Langkah 4.2 − Tambahkan first_ele * max(n, second_ele) kepada jumlah. Di sini, kami menggunakan max(n, second_ele) untuk mengendalikan kes terakhir.
Langkah 4.3 − Tolak second_ele daripada n.
Langkah 5− Kembalikan jumlah maksimum.
Contoh
#include <bits/stdc++.h>
using namespace std;
int getMaxSum(int nums[], int n, int m, int x[], int y[]) {
int maxSum = 0, p;
// To get maximum sum
priority_queue<pair<int, int>> p_que;
// Insert nums[] array pairs into the queue
for (p = 0; p < n; p++)
p_que.push({nums[p], 1});
// Push replacement pairs
for (p = 0; p < m; p++)
p_que.push({y[p], x[p]});
// Add the first N elements of the priority queue in the sum
while (n > 0) {
// Get top element of priority queue
auto temp = p_que.top();
// Remove top element
p_que.pop();
// Add value to the sum
maxSum += temp.first * min(n, temp.second);
// Change N
n -= temp.second;
}
return maxSum;
}
int main() {
int nums[] = {10, 8, 7, 60, 20, 18, 30, 60};
int n = (sizeof nums) / (sizeof nums[0]);
int m = 3;
int x[] = {1, 2, 5};
int y[] = {500, 10, 2};
cout << "The maximum sum we can get by replacing the array values is " << getMaxSum(nums, n, m, x, y);
return 0;
}
Output
The maximum sum we can get by replacing the array values is 708
Kerumitan masa - O(N*logN + m*logm), di mana O(N) dan O(m) digunakan untuk melintasi tatasusunan yang diberikan dan O(logN) digunakan untuk memasukkan dan memadam elemen dalam baris gilir.
Kerumitan ruang - O(N+M) untuk menyimpan pasangan dalam baris gilir.
Dalam kaedah pertama, kita perlu mengisih tatasusunan dalam setiap lelaran untuk mencari unsur x[p] terkecil. Gunakan baris gilir keutamaan untuk mengisih elemen secara automatik semasa ia dimasukkan atau dialih keluar kerana ia menggunakan struktur data timbunan. Oleh itu, ia meningkatkan prestasi kod anda.
Atas ialah kandungan terperinci Jumlah maksimum tatasusunan yang mungkin selepas melakukan operasi yang diberikan. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

AI Hentai Generator
Menjana ai hentai secara percuma.

Artikel Panas

Alat panas

Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma

SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan

Hantar Studio 13.0.1
Persekitaran pembangunan bersepadu PHP yang berkuasa

Dreamweaver CS6
Alat pembangunan web visual

SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)

Topik panas
 1378
1378
 52
52
 Apakah sudo dan mengapa ia penting?
Feb 21, 2024 pm 07:01 PM
Apakah sudo dan mengapa ia penting?
Feb 21, 2024 pm 07:01 PM
sudo (eksekusi superuser) ialah arahan utama dalam sistem Linux dan Unix yang membenarkan pengguna biasa menjalankan perintah tertentu dengan keistimewaan root. Fungsi sudo dicerminkan terutamanya dalam aspek berikut: Menyediakan kawalan kebenaran: sudo mencapai kawalan ketat ke atas sumber sistem dan operasi sensitif dengan membenarkan pengguna mendapatkan kebenaran superuser buat sementara waktu. Pengguna biasa hanya boleh mendapatkan keistimewaan sementara melalui sudo apabila diperlukan, dan tidak perlu log masuk sebagai pengguna super sepanjang masa. Keselamatan yang dipertingkatkan: Dengan menggunakan sudo, anda boleh mengelak daripada menggunakan akaun akar semasa operasi rutin. Menggunakan akaun akar untuk semua operasi boleh menyebabkan kerosakan sistem yang tidak dijangka, kerana sebarang operasi yang salah atau cuai akan mempunyai kebenaran penuh. dan
 Tutorial penggunaan PyCharm: membimbing anda secara terperinci untuk menjalankan operasi
Feb 26, 2024 pm 05:51 PM
Tutorial penggunaan PyCharm: membimbing anda secara terperinci untuk menjalankan operasi
Feb 26, 2024 pm 05:51 PM
PyCharm ialah persekitaran pembangunan bersepadu (IDE) Python yang sangat popular. Ia menyediakan pelbagai fungsi dan alatan untuk menjadikan pembangunan Python lebih cekap dan mudah. Artikel ini akan memperkenalkan anda kepada kaedah operasi asas PyCharm dan menyediakan contoh kod khusus untuk membantu pembaca memulakan dengan cepat dan menjadi mahir dalam mengendalikan alat tersebut. 1. Muat turun dan pasang PyCharm Pertama, kita perlu pergi ke laman web rasmi PyCharm (https://www.jetbrains.com/pyc
 Langkah-langkah operasi dan langkah berjaga-jaga Deploy Linux
Mar 14, 2024 pm 03:03 PM
Langkah-langkah operasi dan langkah berjaga-jaga Deploy Linux
Mar 14, 2024 pm 03:03 PM
Langkah pengendalian dan langkah berjaga-jaga LinuxDeploy LinuxDeploy ialah alat berkuasa yang boleh membantu pengguna menggunakan pelbagai pengedaran Linux dengan pantas pada peranti Android, membolehkan pengguna mengalami sistem Linux yang lengkap pada peranti mudah alih mereka. Artikel ini akan memperkenalkan langkah pengendalian dan langkah berjaga-jaga LinuxDeploy secara terperinci dan memberikan contoh kod khusus untuk membantu pembaca menggunakan alat ini dengan lebih baik. Langkah-langkah operasi: Pasang LinuxDeploy: Pertama, pasang
 Apa yang perlu dilakukan jika anda terlupa menekan F2 untuk kata laluan but win10
Feb 28, 2024 am 08:31 AM
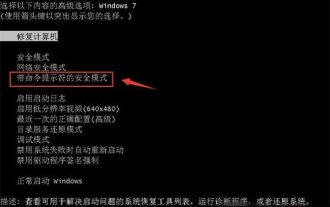
Apa yang perlu dilakukan jika anda terlupa menekan F2 untuk kata laluan but win10
Feb 28, 2024 am 08:31 AM
Mungkin ramai pengguna mempunyai beberapa komputer yang tidak digunakan di rumah, dan mereka telah lupa sepenuhnya kata laluan kuasa hidup kerana mereka tidak digunakan untuk masa yang lama, jadi mereka ingin tahu apa yang perlu dilakukan jika mereka terlupa kata laluan? Kemudian mari kita lihat bersama-sama. Apa yang perlu dilakukan jika anda terlupa menekan F2 untuk kata laluan boot win10 1. Tekan butang kuasa komputer, dan kemudian tekan F2 semasa but (jenama komputer yang berbeza mempunyai butang yang berbeza untuk memasuki BIOS). 2. Dalam antara muka bios, cari pilihan keselamatan (lokasi mungkin berbeza untuk jenama komputer yang berbeza). Biasanya dalam menu tetapan di bahagian atas. 3. Kemudian cari pilihan SupervisorPassword dan klik padanya. 4. Pada masa ini, pengguna boleh melihat kata laluannya, dan pada masa yang sama mencari Didayakan di sebelahnya dan menukarnya kepada Dis.
 Perkongsian langkah operasi tangkapan skrin Huawei Mate60 Pro
Mar 23, 2024 am 11:15 AM
Perkongsian langkah operasi tangkapan skrin Huawei Mate60 Pro
Mar 23, 2024 am 11:15 AM
Dengan populariti telefon pintar, fungsi tangkapan skrin telah menjadi salah satu kemahiran penting untuk kegunaan harian telefon bimbit. Sebagai salah satu telefon mudah alih utama Huawei, fungsi tangkapan skrin Huawei Mate60Pro secara semula jadi telah menarik banyak perhatian daripada pengguna. Hari ini, kami akan berkongsi langkah operasi tangkapan skrin telefon mudah alih Huawei Mate60Pro, supaya semua orang boleh mengambil tangkapan skrin dengan lebih mudah. Pertama sekali, telefon bimbit Huawei Mate60Pro menyediakan pelbagai kaedah tangkapan skrin, dan anda boleh memilih kaedah yang sesuai dengan anda mengikut tabiat peribadi anda. Berikut ialah pengenalan terperinci kepada beberapa pemintasan yang biasa digunakan:
 Bagaimana untuk melumpuhkan butang tindakan pada iPhone 15 Pro dan 15 Pro Max
Nov 07, 2023 am 11:17 AM
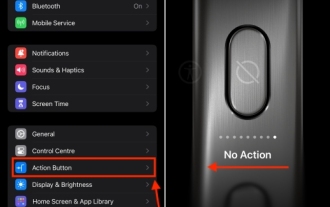
Bagaimana untuk melumpuhkan butang tindakan pada iPhone 15 Pro dan 15 Pro Max
Nov 07, 2023 am 11:17 AM
Apple membawa beberapa ciri perkakasan eksklusif Pro kepada iPhone 15 Pro dan 15 Pro Max, yang menarik perhatian semua orang. Kami bercakap tentang bingkai titanium, reka bentuk anggun, cipset A17 Pro baharu, kanta telefoto 5x yang menarik dan banyak lagi. Daripada semua loceng dan wisel yang ditambahkan pada model iPhone 15 Pro, butang tindakan kekal sebagai ciri yang menonjol dan menonjol. Tidak perlu dikatakan, ia adalah tambahan yang berguna untuk melancarkan tindakan pada iPhone anda. Yang berkata, anda secara tidak sengaja boleh menahan butang Tindakan dan mencetuskan ciri secara tidak sengaja. Terus terang, ia menjengkelkan. Untuk mengelakkan ini, anda harus melumpuhkan butang tindakan pada iPhone 15 Pro dan 15 Pro Max. biarkan
 Pemantauan tatal halaman web CSS: pantau acara tatal halaman web dan lakukan operasi yang sepadan
Nov 18, 2023 am 10:35 AM
Pemantauan tatal halaman web CSS: pantau acara tatal halaman web dan lakukan operasi yang sepadan
Nov 18, 2023 am 10:35 AM
Pemantauan tatal halaman web CSS: pantau acara tatal halaman web dan lakukan operasi yang sepadan Dengan pembangunan berterusan teknologi bahagian hadapan, kesan dan interaksi halaman web menjadi lebih kaya dan pelbagai. Antaranya, pemantauan skrol adalah teknologi biasa yang boleh melakukan beberapa kesan atau operasi khas berdasarkan kedudukan skrol apabila pengguna menatal halaman web. Secara umumnya, pemantauan skrol boleh dilaksanakan melalui JavaScript. Walau bagaimanapun, dalam beberapa kes, kami juga boleh mencapai kesan pemantauan tatal melalui CSS tulen. Artikel ini akan memperkenalkan cara melaksanakan penatalan halaman web melalui CSS
 Butang tindakan tersuai: Terokai pemperibadian pada iPhone 15 Pro
Sep 24, 2023 pm 03:05 PM
Butang tindakan tersuai: Terokai pemperibadian pada iPhone 15 Pro
Sep 24, 2023 pm 03:05 PM
iPhone 15 Pro dan iPhone 15 Pro Max Apple memperkenalkan butang tindakan boleh atur cara baharu yang menggantikan suis dering/senyap tradisional di atas butang kelantangan. Teruskan membaca untuk mengetahui perkara yang dilakukan oleh butang Tindakan dan cara menyesuaikannya. Butang tindakan baharu pada model Apple iPhone 15 Pro menggantikan suis iPhone tradisional yang mengaktifkan Dering dan Senyap. Secara lalai, butang baharu masih akan mengaktifkan kedua-dua fungsi dengan tekan lama, tetapi anda juga boleh meminta tekan lama melaksanakan pelbagai fungsi lain, termasuk akses pantas ke kamera atau lampu suluh, mengaktifkan memo suara, mod fokus, terjemahan dan ciri kebolehaksesan seperti pembesar . Anda juga boleh mengaitkannya dengan satu pintasan, membuka satu tan kemungkinan lain



