Jumlah semua pasangan laluan terpendek dalam pokok itu

Dalam pokok, istilah "jumlah laluan terpendek ke atas semua pasangan nod" merujuk kepada pengiraan jumlah laluan terpendek individu untuk semua pasangan nod. Kaedah yang berkesan ialah menggunakan algoritma dwi DFS (depth first search). Jarak antara nod yang dipilih dan setiap nod lain ditentukan semasa pas DFS pertama. Pokok itu dilalui semula semasa pas DFS kedua, dengan mengambil kira setiap nod sebagai potensi LCA (nenek moyang paling rendah) dan mengira jumlah jarak antara pasangan nod keturunan LCA yang dipilih. Menggunakan kaedah ini, anda boleh mengira jumlah laluan terpendek untuk semua pasangan nod dalam pokok dan memastikan penyelesaian yang ideal
Kaedah penggunaan
Kaedah DFS Berganda (depth first search).
Kaedah pengaturcaraan dinamik
Kaedah Double DFS (Depth First Search)
Untuk jumlah semua pasangan laluan terpendek dalam pepohon, kami menggunakan kaedah DFS (carian pertama mendalam) dwi, yang melibatkan dua pas DFS. Pertama, kita mengira jarak dari mana-mana nod ke semua nod lain. Kemudian, semasa traversal DFS kedua, kami menavigasi pepohon sambil mempertimbangkan setiap nod sebagai LCA yang berpotensi. Kami mengira dan menjumlahkan jarak antara pasangan nod yang merupakan keturunan LCA yang dipilih semasa melintasi. Dengan mengulangi proses ini untuk semua nod, kami memperoleh jumlah semua pasangan laluan terpendek. Strategi ini sangat menarik untuk masalah ini kerana ia secara berkesan mengira jumlah jarak antara semua set nod dalam pepohon.
Algoritma
Sebarang nod dalam pokok boleh digunakan sebagai nod permulaan
Untuk menentukan jarak dari nod permulaan yang dipilih ke semua nod lain, lakukan carian pertama mendalam (DFS) bermula dari nod itu. Jarak ini harus disimpan dalam tatasusunan atau struktur data.
Seterusnya, jalankan carian mendalam-pertama (DFS) kedua pada pepohon, mempertimbangkan setiap nod sebagai kemungkinan nenek moyang sepunya terdekat (LCA)
Semasa melintasi pokok semasa DFS kedua, hitung jarak antara pasangan nod yang merupakan keturunan LCA yang dipilih. Untuk setiap LCA, jarak ini ditambah bersama.
Ulang proses ini untuk setiap nod dalam pokok
Jumlah semua padanan dengan cara yang paling terhingga dalam pokok diwakili oleh jumlah semua jarak yang dikira dalam langkah 4.
Contoh
ialah:Contoh
#include <iostream>
#include <vector>
using namespace std;
const int MAXN = 10005;
vector<int> graph[MAXN];
int ancestor[MAXN];
int dfs(int node, int lca, int distance) {
int sum = 0;
for (int neighbor : graph[node]) {
if (neighbor != lca) {
sum += dfs(neighbor, lca, distance + 1);
}
}
return sum + distance;
}
int main() {
int lca_node = 0;
int total_sum = 0;
for (int node = 0; node < MAXN; ++node) {
if (node != lca_node) {
total_sum += dfs(node, lca_node, 0);
}
}
cout << "Total sum of distances between descendants of the LCA: " << total_sum << endl;
return 0;
}
Output
Total sum of distances between descendants of the LCA: 0
Kaedah pengaturcaraan dinamik:
Kami mula-mula memilih mana-mana nod sebagai nod akar dan menukar pepohon kepada pepohon berakar dalam kaedah pengaturcaraan dinamik, yang digunakan untuk mengira jumlah laluan terpendek antara semua nod dalam pepohon. Kami menggunakan pengaturcaraan dinamik untuk mengira pemisahan antara setiap nod dan nod akar dan menyimpan hasilnya dalam tatasusunan. Kemudian, untuk setiap nod, kami menambah pemisahan (dikira) anak-anaknya daripada nod akar untuk menentukan pemisahan keseluruhan semua nod lain. Dengan cara ini, kita boleh mengira dengan cepat jumlah laluan terpendek antara semua nod. Sebagai cara yang cekap untuk menyelesaikan masalah ini, kerumitan masa algoritma ini ialah O(N), di mana N ialah bilangan nod dalam pokok.
Algoritma
Ambil mana-mana nod dalam pokok sebagai akar dan akar pokok (cth. menggunakan carian mendalam nod akar) untuk mencipta pokok berakar.
Pengaturcaraan dinamik boleh digunakan untuk menentukan jarak setiap nod dari akar. Jarak ini harus disimpan dalam tatasusunan atau struktur data.
Kira jumlah jarak dari setiap nod ke semua nod lain dalam pepohon:
Jumlah semua pasangan laluan terpendek dalam pokok ialah hasil akhir.
a. Lintas nod anak nod semasa.
b. Untuk mempertimbangkan laluan melalui nod semasa, tambahkan bilangan nod dalam subpokok dan jarak ke punca yang dikira sebelum ini untuk setiap subpokok.
c Untuk setiap nod anak nod aktif, tambahkan jumlah ini
d. Tambahkan jumlah nod semasa kepada hasil akhir.
#include <iostream>
#include <vector>
using namespace std;
struct TreeNode {
int val;
vector<TreeNode*> children;
};
int dfs(TreeNode* node, vector<int>& distances) {
int subtree_size = 1;
for (TreeNode* child : node->children) {
subtree_size += dfs(child, distances);
distances[node->val] += distances[child->val] + subtree_size;
}
return subtree_size;
}
int sumOfAllPairShortestPaths(TreeNode* root) {
vector<int> distances(root->val + 1, 0);
dfs(root, distances);
int total_sum = 0;
for (int distance : distances) {
total_sum += distance;
}
return total_sum;
}
int main() {
TreeNode* root = new TreeNode{0};
int result = sumOfAllPairShortestPaths(root);
cout << "Sum of all pair shortest paths in the tree: " << result << endl;
return 0;
}
Output
Sum of all pair shortest paths in the tree: 0
Kesimpulan
Jumlah semua pasangan laluan terpendek dalam pepohon boleh dikira menggunakan kaedah Double DFS (Depth First Search) atau pengaturcaraan dinamik. Kaedah DFS Berganda terdiri daripada dua hantaran, mula-mula mengira jarak dari nod yang dipilih ke semua nod lain, dan kemudian melintasi pepohon itu semula sambil menganggap setiap nod sebagai potensi nenek moyang sepunya terendah (LCA) untuk menjumlahkan jarak antara pasangan nod Keturunan. Kaedah pengaturcaraan dinamik memerlukan secara rekursif menggunakan DFS untuk membina akar pokok dan mengira jarak dari akar ke setiap nod lain. Hasil kedua-dua kaedah adalah sama dan terdiri daripada jumlah semua laluan terpendek berpasangan dalam pokok. Keputusan antara dua algoritma mungkin berdasarkan keutamaan pelaksanaan tertentu atau struktur pokok, tetapi kedua-dua algoritma menyediakan penyelesaian yang cekap.
Atas ialah kandungan terperinci Jumlah semua pasangan laluan terpendek dalam pokok itu. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

Video Face Swap
Tukar muka dalam mana-mana video dengan mudah menggunakan alat tukar muka AI percuma kami!

Artikel Panas

Alat panas

Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma

SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan

Hantar Studio 13.0.1
Persekitaran pembangunan bersepadu PHP yang berkuasa

Dreamweaver CS6
Alat pembangunan web visual

SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)

Topik panas
 1393
1393
 52
52
 1207
1207
 24
24
 Jumlah semua pasangan laluan terpendek dalam pokok itu
Aug 28, 2023 pm 03:17 PM
Jumlah semua pasangan laluan terpendek dalam pokok itu
Aug 28, 2023 pm 03:17 PM
Dalam pokok, istilah "jumlah laluan terpendek bagi semua pasangan nod" merujuk kepada pengiraan jumlah laluan terpendek individu bagi semua pasangan nod. Kaedah yang berkesan ialah menggunakan algoritma dwi DFS (depth first search). Jarak antara nod yang dipilih dan setiap nod lain ditentukan semasa pas DFS pertama. Pokok itu dilalui semula semasa pas DFS kedua, dengan mengambil kira setiap nod sebagai potensi LCA (nenek moyang paling rendah) dan mengira jumlah jarak antara pasangan nod keturunan LCA yang dipilih. Menggunakan kaedah ini, anda boleh mengira jumlah laluan terpendek untuk semua pasangan nod dalam pepohon dan memastikan penyelesaian yang ideal Kaedah yang digunakan kaedah DFS DFS (Depth First Search) Kaedah pengaturcaraan dinamik Kaedah DFS (Depth First Search) untuk pokok. Semua pasangan laluan terpendek
 Bagaimana untuk melaksanakan algoritma laluan terpendek menggunakan java
Sep 19, 2023 am 08:18 AM
Bagaimana untuk melaksanakan algoritma laluan terpendek menggunakan java
Sep 19, 2023 am 08:18 AM
Gambaran keseluruhan cara menggunakan Java untuk melaksanakan algoritma laluan terpendek: Algoritma laluan terpendek ialah aplikasi penting dalam teori graf dan digunakan secara meluas dalam penghalaan rangkaian, navigasi peta dan medan lain. Dalam artikel ini, kita akan belajar cara melaksanakan algoritma laluan terpendek menggunakan Java dan memberikan contoh kod konkrit. Idea algoritma: Terdapat banyak cara untuk melaksanakan algoritma laluan terpendek, antaranya dua algoritma yang paling terkenal ialah algoritma Dijkstra dan algoritma A*. Di sini kita akan memberi tumpuan kepada pelaksanaan algoritma Dijkstra. Asas algoritma Dijkstra
 Penerokaan mendalam tentang kaedah aplikasi dan pelaksanaan struktur data bukan linear pepohon dan graf dalam Java
Dec 26, 2023 am 10:22 AM
Penerokaan mendalam tentang kaedah aplikasi dan pelaksanaan struktur data bukan linear pepohon dan graf dalam Java
Dec 26, 2023 am 10:22 AM
Memahami Pokok dan Graf dalam Java: Meneroka Aplikasi dan Pelaksanaan Struktur Data Tak Linear Pengenalan Dalam sains komputer, struktur data ialah cara data disimpan, disusun dan diuruskan dalam komputer. Struktur data boleh dibahagikan kepada struktur data linear dan struktur data bukan linear. Pokok dan graf ialah dua jenis struktur data tak linear yang paling biasa digunakan. Artikel ini akan menumpukan pada konsep, aplikasi dan pelaksanaan pepohon dan graf dalam Java, dan memberikan contoh kod khusus. Konsep dan Aplikasi Pokok Pokok ialah jenis data abstrak, koleksi nod dan tepi. Setiap nod pokok mengandungi nombor
 Penggunaan rekursi yang hebat dalam struktur data C++: pelaksanaan tindanan dan pokok
May 04, 2024 pm 01:54 PM
Penggunaan rekursi yang hebat dalam struktur data C++: pelaksanaan tindanan dan pokok
May 04, 2024 pm 01:54 PM
Aplikasi rekursi dalam struktur data C++: Tindanan: Tindanan dilaksanakan secara rekursif melalui struktur masuk-dahulu-keluar (LIFO). Pokok: Pokok dilaksanakan secara rekursif melalui struktur hierarki, menyokong operasi seperti sisipan dan pengiraan kedalaman. Rekursi menyediakan penyelesaian yang ringkas dan cekap untuk memproses struktur bersarang, menjadikan pelaksanaan struktur data lebih intuitif dan lebih mudah untuk diselenggara.
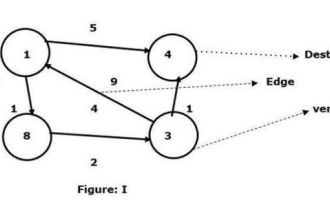 Cari laluan terpendek antara mana-mana dua nod menggunakan algoritma Floyd-Warshal
Sep 20, 2023 pm 02:21 PM
Cari laluan terpendek antara mana-mana dua nod menggunakan algoritma Floyd-Warshal
Sep 20, 2023 pm 02:21 PM
C++ mempunyai makro, yang ditakrifkan sebagai sekeping kod atau nilai yang dijangkakan, dan ia akan digunakan semula apabila pengguna memerlukannya. Algoritma Floyd-Walshall ialah proses mencari laluan terpendek antara semua pasangan bucu dalam graf berwajaran tertentu. Algoritma mengikut pendekatan pengaturcaraan dinamik untuk mencari graf berat minimum. Marilah kita memahami maksud algoritma Floyd-Walshall melalui rajah - ambil bucu 1 sebagai sumber dan bucu 4 sebagai destinasi dan cari laluan terpendek di antara mereka. Kami telah melihat bahawa terdapat dua laluan yang boleh disambungkan ke bucu sasaran 4. 1->4 – tepi mempunyai berat 51->8->3->4 – berat tepi (1+2+1) ialah 4. Dalam graf I yang diberikan, kita melihat tepi terkecil yang menghubungkan dua bucu. Jadi di sini puncaknya
 Idea reka bentuk algoritma PHP: Bagaimana untuk mencapai penyelesaian yang cekap kepada masalah laluan terpendek graf?
Sep 19, 2023 pm 03:43 PM
Idea reka bentuk algoritma PHP: Bagaimana untuk mencapai penyelesaian yang cekap kepada masalah laluan terpendek graf?
Sep 19, 2023 pm 03:43 PM
Idea reka bentuk algoritma PHP: Bagaimana untuk mencapai penyelesaian yang cekap kepada masalah laluan terpendek graf? Dalam pembangunan sebenar, kita selalunya perlu menyelesaikan masalah laluan terpendek, seperti dalam navigasi peta, penghalaan rangkaian, pengedaran logistik dan bidang lain. Algoritma laluan terpendek untuk graf adalah kunci untuk menyelesaikan jenis masalah ini. Graf terdiri daripada satu set bucu dan satu set tepi. Bucu mewakili nod, dan tepi mewakili hubungan antara nod. Masalah laluan terpendek ialah mencari laluan terpendek yang menghubungkan dua nod. Dalam PHP, kita boleh menggunakan pelbagai algoritma untuk menyelesaikan masalah laluan terpendek, yang paling terkenal ialah
 Gunakan C++ untuk memadam semua nod yang tidak berada di mana-mana laluan dan jumlah laluan adalah kurang daripada k
Sep 04, 2023 am 10:17 AM
Gunakan C++ untuk memadam semua nod yang tidak berada di mana-mana laluan dan jumlah laluan adalah kurang daripada k
Sep 04, 2023 am 10:17 AM
Dalam masalah ini, kita mempunyai pokok binari yang laluannya dari nod akar ke nod daun ditakrifkan sepenuhnya. Jumlah semua nod dari nod akar ke nod daun mestilah lebih besar daripada atau sama dengan k. Jadi kita perlu memadam semua nod dalam laluan yang jumlahnya kurang daripada k. Perkara penting yang perlu diingat di sini ialah nod mungkin sebahagian daripada banyak laluan, jadi hanya jika jumlah semua laluan yang tinggal ialah 10+20+5, iaitu 25, iaitu kurang daripada 150, kita perlu memangkasnya dan mengalih keluar 5 . Selepas itu, mari kita nilai 10->30->40. Ia kurang daripada 150, jadi padamkan 40. Sekarang kita melihat laluan lain 10->20->35->50 dan jumlah 115 adalah kurang daripada 150, jadi
 Program C++ untuk mengalih keluar nod yang tidak memenuhi laluan dan lebih besar daripada atau sama dengan k
Sep 14, 2023 am 11:25 AM
Program C++ untuk mengalih keluar nod yang tidak memenuhi laluan dan lebih besar daripada atau sama dengan k
Sep 14, 2023 am 11:25 AM
Dalam masalah ini, kita mempunyai pokok binari yang laluannya dari nod akar ke nod daun ditakrifkan sepenuhnya. Jumlah semua nod dari nod akar ke nod daun mestilah lebih besar daripada atau sama dengan nilai malar k. Oleh itu, kita perlu memadam semua nod dalam laluan tersebut yang jumlahnya kurang daripada k, supaya laluan yang tinggal dalam pepohon akan lebih besar daripada k. Perkara penting yang perlu diingat di sini ialah nod mungkin sebahagian daripada banyak laluan, jadi hanya jika jumlah semua laluan yang menuju ke nod itu, kiri, berjumlah 10+20+5, iaitu 25, kurang daripada 150, kita perlukan untuk memangkas dan mengeluarkan 5. Selepas itu, mari kita nilai 10->30->40. Ia kurang daripada 150, jadi 40 dipadamkan. Sekarang kita lihat laluan lain 10->20-




