
Di sini kita akan melihat cara mengira luas poligon sekata bersisi-n bagi jejari yang diberikan. Jejari di sini ialah jarak dari mana-mana bucu ke pusat. Untuk menyelesaikan masalah ini, kami melukis garis menegak dari tengah ke salah satu sisi. Andaikan panjang setiap sisi ialah 'a'. Serenjang membahagi sisi kepada dua bahagian, setiap bahagian mempunyai panjang a/2. Garis menegak dan jejari membentuk sudut x. Katakan panjang jejari ialah h.
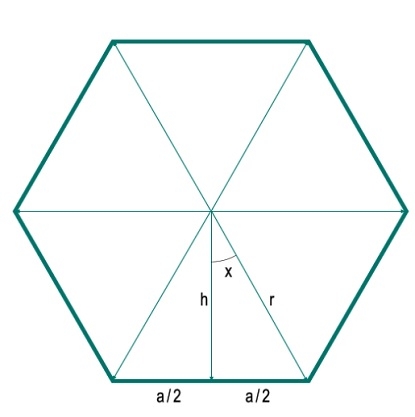
Di sini, kita dapat melihat bahawa poligon dibahagikan kepada N segi tiga sama. Oleh itu, bagi mana-mana poligon dengan sisi N, ia akan dibahagikan kepada N segi tiga. Oleh itu, sudut di pusat ialah 360 darjah. Ini dibahagikan kepada 360°/N sudut yang berbeza (di sini 360°/6 = 60°). Oleh itu, sudut x ialah 180°/N. Sekarang kita boleh mendapatkan h dan a dengan mudah menggunakan persamaan trigonometri.
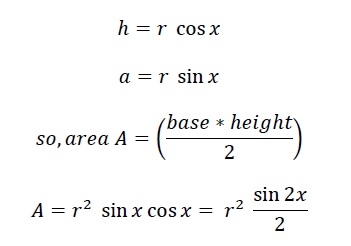
Kini luas keseluruhan poligon ialah N*A.
#include <iostream>
#include <cmath>
using namespace std;
float polygonArea(float r, int n){
return ((r * r * n) * sin((360 / n) * 3.1415 / 180)) / 2; //convert
angle to rad then calculate
}
int main() {
float rad = 9.0f;
int sides = 6;
cout << "Polygon Area: " << polygonArea(rad, sides);
}Polygon Area: 210.44
Atas ialah kandungan terperinci Apakah luas poligon sekata bersisi-n bagi jejari tertentu?. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
 Apakah kaedah pembundaran dalam sql
Apakah kaedah pembundaran dalam sql
 Bagaimana untuk membuka fail html WeChat
Bagaimana untuk membuka fail html WeChat
 Pengenalan kepada perisian lukisan seni bina
Pengenalan kepada perisian lukisan seni bina
 Cara membuat gambar bulat dalam ppt
Cara membuat gambar bulat dalam ppt
 Bagaimana untuk menyelesaikan masalah 400 permintaan buruk apabila halaman web dipaparkan
Bagaimana untuk menyelesaikan masalah 400 permintaan buruk apabila halaman web dipaparkan
 Teknik yang biasa digunakan untuk perangkak web
Teknik yang biasa digunakan untuk perangkak web
 Penggunaan arahan sumber dalam linux
Penggunaan arahan sumber dalam linux
 Bagaimana untuk membuka fail keadaan
Bagaimana untuk membuka fail keadaan




