Algoritma Tomohiko Sakamoto - mencari hari dalam seminggu

Dalam artikel ini, kita akan membincangkan apakah algoritma Tomohiko Sakamoto dan cara menggunakannya untuk mengenal pasti hari dalam minggu tarikh tertentu. Terdapat beberapa algoritma untuk mengetahui hari dalam seminggu, tetapi algoritma ini adalah yang paling berkuasa. Algoritma ini mencari hari dalam bulan di mana tarikh ini berlaku dalam masa sekecil mungkin dan dengan kerumitan ruang terkecil.
Pernyataan Masalah - Kami diberi tarikh berdasarkan kalendar Georgia dan tugas kami adalah untuk mengetahui hari dalam minggu tarikh yang diberikan menggunakan algoritma Tomohiko Sakamoto.
Contoh
Masukkan - Tarikh = 30, Bulan = 04, Tahun = 2020
Output - Tarikh yang diberikan ialah Isnin
Masukkan - Tarikh = 15, Bulan = 03, Tahun = 2012
Output - Tarikh yang diberikan ialah Khamis
Masukkan - tarikh = 24, bulan = 12, tahun = 2456
Output - Tarikh yang diberikan ialah Ahad
Algoritma Sakamoto Tomohiko
Sekarang mari kita bincangkan gerak hati di sebalik algoritma Tomohiko Sakamoto.
Seperti yang kita sedia maklum, mengikut kalendar Georgia, 1 Januari Masihi jatuh pada hari Isnin.
Kes 1 abaikan tahun lompat
Kami mula-mula membincangkan kes di mana semua tahun lompat diabaikan, iaitu terdapat 365 hari dalam setahun.
Memandangkan Januari ada 31 hari dan seminggu ada 7 hari, kita boleh katakan Januari ada 7*4 + 3 hari, bermakna hari pertama bulan Februari sentiasa 3 hari selepas hari pertama langit Januari. p>
Memandangkan Februari mempunyai 28 hari (kecuali tahun lompat), yang merupakan gandaan 7, kita boleh mengatakan bahawa 1 Mac adalah pada hari yang sama dengan 1 Februari, yang bermaksud bahawa 1 Mac juga akan menjadi 3 Hari selepas 1 Januari.
Kini, untuk April, Mac mempunyai 31 hari, iaitu 7*4 +3, bermakna ia akan berlaku 3 hari selepas 1 Mac. Oleh itu, kita boleh mengatakan bahawa 1 April akan berlaku 6 hari selepas 1 Januari.
Kami kini akan membina tatasusunan dengan arr[i] mewakili bilangan hari tambahan selepas bulan i berlaku berbanding 1 Januari.
Kami ada arr[] = {0, 3, 3, 6, 1, 4, 6, 2, 5, 0, 3, 5}.
Kes 2 Tahun Lompat
Sekarang mari kita bincangkan situasi tahun lompat.
Setiap empat tahun, satu hari ditambah kepada pengiraan kami, tetapi bukan setiap seratus tahun. Kita perlu mengambil kira hari-hari tambahan ini. Untuk ini kami akan menggunakan formula -
Tahun/4 (Setiap 4 tahun)
– Tahun / 100 (untuk setiap 100 tahun iaitu gandaan 4 tetapi masih bukan tahun lompat, kami mengeluarkannya daripada tahun lompat)
+ tahun / 400 (setiap tahun ke-400, ia adalah gandaan 100, tetapi masih tahun berulang)
Formula ini akan memberikan kita bilangan tahun lompat yang tepat. Walau bagaimanapun, terdapat satu pengecualian.
Kini, kita tahu bahawa 29 Februari dianggap sebagai hari lompat, bukan 0 Januari.
Ini bermakna kita tidak perlu memasukkan dua bulan pertama dalam tahun dalam pengiraan kerana hari lompat tidak mempunyai kesan ke atasnya. Jadi jika Januari atau Februari, kita akan tolak 1 daripada tahun itu untuk membayar pampasan. Oleh itu, dalam bulan-bulan ini, nilai tahun/4 hendaklah berdasarkan tahun sebelumnya dan bukannya tahun semasa.
Untuk menyelesaikan masalah tahun lompat, kita boleh menolak 1 daripada nilai arr[] setiap bulan selepas Februari untuk mengisi kekosongan. Ini menyelesaikan masalah tahun lompat. Kita perlu membuat perubahan berikut pada algoritma supaya ia berfungsi dalam tahun lompat dan tahun rata.
arr[] = { 0, 3, 2, 5, 0, 3, 5, 1, 4, 6, 2, 4 }
Jika bulan semasa ialah Januari atau Februari, kita perlu menolak 1 daripada tahun tersebut.
Kita perlu mengubah suai kenaikan tahun dalam modulus kepada tahun +tahun/4 –tahun/100 +tahun/400 dan bukannya tahun. Perubahan ini perlu untuk mengambil kira hari tambahan dalam tahun lompat dan melaraskan pengiraan dengan sewajarnya.
Contoh
Kod untuk kaedah ini ialah:
#include <bits/stdc++.h>
using namespace std;
// code to find out the day number of the given date
int Weekday(int year, int month, int day) {
int arr[] = { 0, 3, 2, 5, 0, 3, 5, 1, 4, 6, 2, 4 };
if ( month < 3 )
year -= 1;
return ( ( year + year / 4 - year / 100 + year / 400 + arr[month - 1] + day) % 7 );
}
int main(void) {
int day = 9, month = 9, year = 2020;
int d = Weekday(year, month, day);
string days[] = { "Sunday", "Monday", "Tuesday", "Wednesday", "Thursday", "Friday", "Saturday" };
cout<< " The given date is on ";
cout << days[d];
return 0;
}
Output
The given date is on Wednesday
kerumitan
Kerumitan Masa - Kerumitan masa kaedah ini ialah O(1)
Kerumitan Ruang - Kerumitan ruang kaedah ini ialah O(1) kerana kami tidak menggunakan sebarang ruang tambahan.
Kesimpulan - Dalam artikel ini, kami membincangkan algoritma Tomohiko Sakamoto dan intuisi di belakangnya
Atas ialah kandungan terperinci Algoritma Tomohiko Sakamoto - mencari hari dalam seminggu. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

AI Hentai Generator
Menjana ai hentai secara percuma.

Artikel Panas

Alat panas

Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma

SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan

Hantar Studio 13.0.1
Persekitaran pembangunan bersepadu PHP yang berkuasa

Dreamweaver CS6
Alat pembangunan web visual

SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)

Topik panas
 1378
1378
 52
52
 CLIP-BEVFormer: Selia secara eksplisit struktur BEVFormer untuk meningkatkan prestasi pengesanan ekor panjang
Mar 26, 2024 pm 12:41 PM
CLIP-BEVFormer: Selia secara eksplisit struktur BEVFormer untuk meningkatkan prestasi pengesanan ekor panjang
Mar 26, 2024 pm 12:41 PM
Ditulis di atas & pemahaman peribadi penulis: Pada masa ini, dalam keseluruhan sistem pemanduan autonomi, modul persepsi memainkan peranan penting Hanya selepas kenderaan pemanduan autonomi yang memandu di jalan raya memperoleh keputusan persepsi yang tepat melalui modul persepsi boleh Peraturan hiliran dan. modul kawalan dalam sistem pemanduan autonomi membuat pertimbangan dan keputusan tingkah laku yang tepat pada masanya dan betul. Pada masa ini, kereta dengan fungsi pemanduan autonomi biasanya dilengkapi dengan pelbagai penderia maklumat data termasuk penderia kamera pandangan sekeliling, penderia lidar dan penderia radar gelombang milimeter untuk mengumpul maklumat dalam modaliti yang berbeza untuk mencapai tugas persepsi yang tepat. Algoritma persepsi BEV berdasarkan penglihatan tulen digemari oleh industri kerana kos perkakasannya yang rendah dan penggunaan mudah, dan hasil keluarannya boleh digunakan dengan mudah untuk pelbagai tugas hiliran.
 Melaksanakan Algoritma Pembelajaran Mesin dalam C++: Cabaran dan Penyelesaian Biasa
Jun 03, 2024 pm 01:25 PM
Melaksanakan Algoritma Pembelajaran Mesin dalam C++: Cabaran dan Penyelesaian Biasa
Jun 03, 2024 pm 01:25 PM
Cabaran biasa yang dihadapi oleh algoritma pembelajaran mesin dalam C++ termasuk pengurusan memori, multi-threading, pengoptimuman prestasi dan kebolehselenggaraan. Penyelesaian termasuk menggunakan penunjuk pintar, perpustakaan benang moden, arahan SIMD dan perpustakaan pihak ketiga, serta mengikuti garis panduan gaya pengekodan dan menggunakan alat automasi. Kes praktikal menunjukkan cara menggunakan perpustakaan Eigen untuk melaksanakan algoritma regresi linear, mengurus memori dengan berkesan dan menggunakan operasi matriks berprestasi tinggi.
 Terokai prinsip asas dan pemilihan algoritma bagi fungsi isihan C++
Apr 02, 2024 pm 05:36 PM
Terokai prinsip asas dan pemilihan algoritma bagi fungsi isihan C++
Apr 02, 2024 pm 05:36 PM
Lapisan bawah fungsi C++ sort menggunakan isihan gabungan, kerumitannya ialah O(nlogn), dan menyediakan pilihan algoritma pengisihan yang berbeza, termasuk isihan pantas, isihan timbunan dan isihan stabil.
 Bolehkah kecerdasan buatan meramalkan jenayah? Terokai keupayaan CrimeGPT
Mar 22, 2024 pm 10:10 PM
Bolehkah kecerdasan buatan meramalkan jenayah? Terokai keupayaan CrimeGPT
Mar 22, 2024 pm 10:10 PM
Konvergensi kecerdasan buatan (AI) dan penguatkuasaan undang-undang membuka kemungkinan baharu untuk pencegahan dan pengesanan jenayah. Keupayaan ramalan kecerdasan buatan digunakan secara meluas dalam sistem seperti CrimeGPT (Teknologi Ramalan Jenayah) untuk meramal aktiviti jenayah. Artikel ini meneroka potensi kecerdasan buatan dalam ramalan jenayah, aplikasi semasanya, cabaran yang dihadapinya dan kemungkinan implikasi etika teknologi tersebut. Kecerdasan Buatan dan Ramalan Jenayah: Asas CrimeGPT menggunakan algoritma pembelajaran mesin untuk menganalisis set data yang besar, mengenal pasti corak yang boleh meramalkan di mana dan bila jenayah mungkin berlaku. Set data ini termasuk statistik jenayah sejarah, maklumat demografi, penunjuk ekonomi, corak cuaca dan banyak lagi. Dengan mengenal pasti trend yang mungkin terlepas oleh penganalisis manusia, kecerdasan buatan boleh memperkasakan agensi penguatkuasaan undang-undang
 Di manakah tempat di mana cahaya lilin bersinar di Destiny Ark?
Mar 20, 2024 pm 05:46 PM
Di manakah tempat di mana cahaya lilin bersinar di Destiny Ark?
Mar 20, 2024 pm 05:46 PM
Pembukaan versi baru peta Ark of Destiny juga mempunyai misi reputasi baru Selain peta Rowan, terdapat juga misi harian di Pulau Wisdom mencapai matlamat "mencari peta yang betul". Tiada panduan untuk pautan ini "Tempat cahaya lilin". Destiny Ark untuk mencari tempat di mana cahaya lilin bersinar adalah di dalam bilik di Pulau Kebijaksanaan Terdapat juga koridor di dalam dewan, yang boleh menuju ke ruang bawah tanah, anda boleh melihat lokasi tugas-tugas berikutnya. seperti yang ditunjukkan dalam gambar:
 Algoritma pengesanan yang dipertingkatkan: untuk pengesanan sasaran dalam imej penderiaan jauh optik resolusi tinggi
Jun 06, 2024 pm 12:33 PM
Algoritma pengesanan yang dipertingkatkan: untuk pengesanan sasaran dalam imej penderiaan jauh optik resolusi tinggi
Jun 06, 2024 pm 12:33 PM
01Garis prospek Pada masa ini, sukar untuk mencapai keseimbangan yang sesuai antara kecekapan pengesanan dan hasil pengesanan. Kami telah membangunkan algoritma YOLOv5 yang dipertingkatkan untuk pengesanan sasaran dalam imej penderiaan jauh optik resolusi tinggi, menggunakan piramid ciri berbilang lapisan, strategi kepala pengesanan berbilang dan modul perhatian hibrid untuk meningkatkan kesan rangkaian pengesanan sasaran dalam imej penderiaan jauh optik. Menurut set data SIMD, peta algoritma baharu adalah 2.2% lebih baik daripada YOLOv5 dan 8.48% lebih baik daripada YOLOX, mencapai keseimbangan yang lebih baik antara hasil pengesanan dan kelajuan. 02 Latar Belakang & Motivasi Dengan perkembangan pesat teknologi penderiaan jauh, imej penderiaan jauh optik resolusi tinggi telah digunakan untuk menggambarkan banyak objek di permukaan bumi, termasuk pesawat, kereta, bangunan, dll. Pengesanan objek dalam tafsiran imej penderiaan jauh
 Aplikasi algoritma dalam pembinaan 58 platform potret
May 09, 2024 am 09:01 AM
Aplikasi algoritma dalam pembinaan 58 platform potret
May 09, 2024 am 09:01 AM
1. Latar Belakang Pembinaan 58 Portrait Platform Pertama sekali, saya ingin berkongsi dengan anda latar belakang pembinaan 58 Portrait Platform. 1. Pemikiran tradisional platform pemprofilan tradisional tidak lagi mencukupi Membina platform pemprofilan pengguna bergantung pada keupayaan pemodelan gudang data untuk menyepadukan data daripada pelbagai barisan perniagaan untuk membina potret pengguna yang tepat untuk memahami tingkah laku, minat pengguna dan keperluan, dan menyediakan keupayaan sampingan, akhirnya, ia juga perlu mempunyai keupayaan platform data untuk menyimpan, bertanya dan berkongsi data profil pengguna dan menyediakan perkhidmatan profil dengan cekap. Perbezaan utama antara platform pemprofilan perniagaan binaan sendiri dan platform pemprofilan pejabat pertengahan ialah platform pemprofilan binaan sendiri menyediakan satu barisan perniagaan dan boleh disesuaikan atas permintaan platform pertengahan pejabat berkhidmat berbilang barisan perniagaan, mempunyai kompleks pemodelan, dan menyediakan lebih banyak keupayaan umum. 2.58 Potret pengguna latar belakang pembinaan potret di platform tengah 58
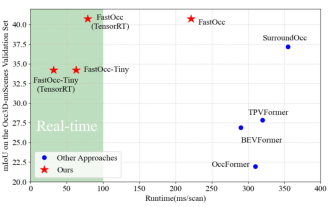 Tambah SOTA dalam masa nyata dan meroket! FastOcc: Inferens yang lebih pantas dan algoritma Occ mesra penggunaan sudah tersedia!
Mar 14, 2024 pm 11:50 PM
Tambah SOTA dalam masa nyata dan meroket! FastOcc: Inferens yang lebih pantas dan algoritma Occ mesra penggunaan sudah tersedia!
Mar 14, 2024 pm 11:50 PM
Ditulis di atas & Pemahaman peribadi penulis ialah dalam sistem pemanduan autonomi, tugas persepsi adalah komponen penting dalam keseluruhan sistem pemanduan autonomi. Matlamat utama tugas persepsi adalah untuk membolehkan kenderaan autonomi memahami dan melihat elemen persekitaran sekeliling, seperti kenderaan yang memandu di jalan raya, pejalan kaki di tepi jalan, halangan yang dihadapi semasa memandu, tanda lalu lintas di jalan raya, dan sebagainya, dengan itu membantu hiliran. modul Membuat keputusan dan tindakan yang betul dan munasabah. Kenderaan dengan keupayaan pemanduan autonomi biasanya dilengkapi dengan pelbagai jenis penderia pengumpulan maklumat, seperti penderia kamera pandangan sekeliling, penderia lidar, penderia radar gelombang milimeter, dsb., untuk memastikan kenderaan autonomi itu dapat melihat dan memahami persekitaran sekeliling dengan tepat. elemen , membolehkan kenderaan autonomi membuat keputusan yang betul semasa pemanduan autonomi. kepala




