 pembangunan bahagian belakang
pembangunan bahagian belakang
 C++
C++
 Dalam C++, cari bilangan operasi yang diperlukan untuk menjadikan semua elemen tatasusunan sama
Dalam C++, cari bilangan operasi yang diperlukan untuk menjadikan semua elemen tatasusunan sama
Dalam C++, cari bilangan operasi yang diperlukan untuk menjadikan semua elemen tatasusunan sama

Dalam masalah ini, kita mendapat array arr saiz n. Tugas kami ialah untuk mencari bilangan operasi yang diperlukan untuk menjadikan semua elemen tatasusunan sama
Operasi ditakrifkan sebagai mengagihkan elemen tatasusunan daripada elemen dengan berat terbesar kepada berat yang sama semua elemen.
Jika tidak mungkin untuk membuat elemen tatasusunan sama, cetak -1.
Mari kita ambil contoh untuk memahami masalah ini,
Input : arr[] = {7, 3, 3, 3}
Output : 3Penjelasan
Tatasusunan yang diperuntukkan ialah {4, 4, 4, 4}
Penyelesaian
Cara mudah untuk menyelesaikan masalah ini nilai maksimum tatasusunan. Nilai maksimum ini kemudiannya digunakan untuk menyemak sama ada semua elemen tatasusunan adalah sama, dan jika nilai itu sama dengan nilai maksimum tatasusunan tolak n (atau gandaan daripadanya). Jika ya, n dikembalikan, jika tidak, -1 dikembalikan (menunjukkan bahawa ia tidak mungkin).
Contoh
Mari kita ambil contoh untuk memahami masalahnya
#include<bits/stdc++.h>
using namespace std;
int findOperationCount(int arr[],int n){
int j = 0, operations = 0;
int maxVal = arr[0];
int minVal = arr[0];
int maxValInd = 0;
for (int i = 1; i < n; i++){
if(arr[i] > maxVal){
maxVal = arr[i];
maxValInd = i;
}
if(arr[i] < minVal){
minVal = arr[i];
}
}
for (int i =0;i<n;i++){
if (arr[i] != maxVal && arr[i] <= minVal && arr[i] != 0){
arr[j] += 1;
arr[maxValInd] -= 1;
maxVal -= 1;
operations += 1;
j += 1;
}
else if (arr[i] != 0){
j += 1;
}
}
for (int i = 0; i < n; i++){
if (arr[i] != maxVal){
operations = -1;
break;
}
}
return operations;
}
int main(){
int arr[] = {4, 4, 8, 4};
int n = sizeof(arr)/sizeof(arr[0]);
cout<<"The number of operations required to make all array elements Equal is "<<findOperationCount(arr, n);
return 0;
}Output
The number of operations required to make all array elements Equal is 3
Atas ialah kandungan terperinci Dalam C++, cari bilangan operasi yang diperlukan untuk menjadikan semua elemen tatasusunan sama. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

Video Face Swap
Tukar muka dalam mana-mana video dengan mudah menggunakan alat tukar muka AI percuma kami!

Artikel Panas

Alat panas

Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma

SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan

Hantar Studio 13.0.1
Persekitaran pembangunan bersepadu PHP yang berkuasa

Dreamweaver CS6
Alat pembangunan web visual

SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)

Topik panas
 Gunakan C++ untuk menulis kod untuk mencari nombor bukan persegi Nth
Aug 30, 2023 pm 10:41 PM
Gunakan C++ untuk menulis kod untuk mencari nombor bukan persegi Nth
Aug 30, 2023 pm 10:41 PM
Kita semua tahu nombor yang bukan kuasa dua mana-mana nombor, seperti 2, 3, 5, 7, 8, dll. Terdapat N nombor bukan persegi, dan adalah mustahil untuk mengetahui setiap nombor. Jadi, dalam artikel ini, kami akan menerangkan segala-galanya tentang nombor tanpa kuasa dua atau bukan kuasa dua dan cara untuk mencari nombor bukan kuasa dua N dalam C++. Nombor bukan kuasa dua ken Jika nombor ialah kuasa dua integer, maka nombor itu dipanggil kuasa dua sempurna. Beberapa contoh nombor kuasa dua sempurna ialah -1isquareof14issquareof29issquareof316issquareof425issquareof5 Jika nombor bukan kuasa dua mana-mana integer, maka nombor itu dipanggil bukan kuasa dua. Sebagai contoh, 15 nombor bukan kuasa dua yang pertama ialah -2,3,5,6,
 Algoritma penyongsangan untuk putaran kanan tatasusunan yang ditulis dalam C++
Sep 08, 2023 pm 08:17 PM
Algoritma penyongsangan untuk putaran kanan tatasusunan yang ditulis dalam C++
Sep 08, 2023 pm 08:17 PM
Dalam artikel ini, kita akan mempelajari tentang algoritma pembalikan untuk memutar tatasusunan yang diberikan ke kanan dengan elemen k, contohnya −Input:arr[]={4,6,2,6,43,7,3,7}, k= 4Output:{43,7,3,7,4,6,2,6}Penjelasan:Pusingeachelementofarrayby4-elementtotherightmemberi{43,7,3,7,4,6,2,6}.Input:arr[]= {8 ,5,8,2,1,4,9,3},k=3Output:{4,9,3,8,5,8,2,1} Cari penyelesaian
 Dalam pengaturcaraan C, cari luas bulatan
Aug 25, 2023 pm 10:57 PM
Dalam pengaturcaraan C, cari luas bulatan
Aug 25, 2023 pm 10:57 PM
Bulatan ialah rajah tertutup. Semua titik pada bulatan adalah sama jarak dari titik di dalam bulatan. Titik tengah dipanggil pusat bulatan. Jarak dari satu titik ke pusat bulatan dipanggil jejari. Luas ialah perwakilan kuantitatif bagi rentang dimensi bagi rajah tertutup. Luas bulatan ialah kawasan yang tertutup dalam dimensi bulatan. Formula untuk mengira luas bulatan, Luas=π*r*r Untuk mengira luas, kami memberikan jejari bulatan sebagai input, kami akan menggunakan formula untuk mengira luas, algoritma LANGKAH1: Takeradiusasinputfromtheuserusingstdinput.STEP2 : Kirakaluas bulatan, luas=(
 Ditulis dalam C++, cari bilangan empat kali ganda yang tiga sebutan pertamanya ialah jujukan aritmetik dan tiga sebutan terakhir ialah jujukan geometri.
Aug 30, 2023 pm 02:09 PM
Ditulis dalam C++, cari bilangan empat kali ganda yang tiga sebutan pertamanya ialah jujukan aritmetik dan tiga sebutan terakhir ialah jujukan geometri.
Aug 30, 2023 pm 02:09 PM
Dalam artikel ini kami akan menerangkan semua cara yang mungkin untuk mencari kuarteron, menggunakan A.P. untuk 3 sebutan pertama dan G.P. untuk 3 sebutan terakhir. Pertama, kami akan menerangkan definisi asas janjang aritmetik (A.P.) dan janjang geometri (G.P.). Kemajuan Aritmetik (A.P.) - Ia adalah urutan nombor di mana perbezaan sepunya (d) adalah sama atau malar, bermakna perbezaan dua nombor berturut-turut adalah malar. Contohnya: 1,3,5,7,9|d=2 Kemajuan Geometrik (G.P.) - Ini ialah jujukan nombor di mana nisbah sepunya (r) adalah sama, yang bermaksud kita boleh mendarab nombor sebelumnya dengan tetap nombor. Contohnya: 3, 6, 12, 24, ....|r=2 Dalam masalah ini, kita perlu menentukan berapa banyak dalam array arr[] bagi N integer
 Tulis kod menggunakan C++ untuk mencari bilangan subarray dengan nilai minimum dan maksimum yang sama
Aug 25, 2023 pm 11:33 PM
Tulis kod menggunakan C++ untuk mencari bilangan subarray dengan nilai minimum dan maksimum yang sama
Aug 25, 2023 pm 11:33 PM
Dalam artikel ini, kami akan menggunakan C++ untuk menyelesaikan masalah mencari bilangan subarray yang nilai maksimum dan minimumnya adalah sama. Berikut ialah contoh masalah −Input:array={2,3,6,6,2,4,4,4}Output:12Penjelasan:{2},{3},{6},{6}, {2 },{4},{4},{4},{6,6},{4,4},{4,4}dan{4,4,4}arethesubarraysyang boleh dibentuk denganmaksimumdanminimumelemensama.Input:array={3, 3, 1,5,
 Cari bilangan pasangan unik dalam tatasusunan menggunakan C++
Sep 07, 2023 am 11:53 AM
Cari bilangan pasangan unik dalam tatasusunan menggunakan C++
Sep 07, 2023 am 11:53 AM
Kami memerlukan pengetahuan yang betul untuk mencipta beberapa pasangan unik dalam sintaks tatasusunan C++. Semasa mencari bilangan pasangan unik, kami mengira semua pasangan unik dalam tatasusunan yang diberikan iaitu semua pasangan yang mungkin boleh dibentuk di mana setiap pasangan harus unik. Contohnya -Input:array[]={5,5,9}Output:4Explanation:Thenumberofalluniquepairsare(5,5),(5,9),(9,5)and(9,9).Input:array[] = {5,4,3,2,2}Output:16 Cara Mencari Penyelesaian Terdapat dua cara untuk menyelesaikan masalah ini, iaitu −
 Balikkan kumpulan senarai pautan berganda mengikut saiz yang diberikan menggunakan C++
Sep 04, 2023 am 09:49 AM
Balikkan kumpulan senarai pautan berganda mengikut saiz yang diberikan menggunakan C++
Sep 04, 2023 am 09:49 AM
Dalam masalah ini, kita diberikan penunjuk kepada kepala senarai terpaut dan integer k. Dalam kumpulan saiz k, kita perlu membalikkan senarai terpaut. Contohnya -Input:1<->2<->3<->4<->5(doublylinkedlist),k=3Output:3<->2<->1<->5<->4 mencari penyelesaian Kaedah Dalam masalah ini, kami akan merumuskan algoritma rekursif untuk menyelesaikan masalah ini. Dalam kaedah ini kita akan menggunakan rekursi dan menyelesaikan masalah menggunakan rekursi. Contoh#include<iostream&
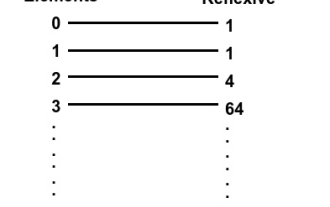 Ditulis dalam C++, cari bilangan hubungan refleksif pada set
Aug 26, 2023 pm 08:17 PM
Ditulis dalam C++, cari bilangan hubungan refleksif pada set
Aug 26, 2023 pm 08:17 PM
Dalam artikel ini kami akan menerangkan cara untuk mencari hubungan refleksif pada set. Dalam masalah ini, kita diberi nombor n, dan set n nombor asli, dan kita mesti menentukan bilangan hubungan refleksif. Hubungan refleksif - Suatu hubungan R dikatakan sebagai hubungan refleksif pada set A jika bagi setiap 'a' dalam set A, (a, a) tergolong dalam hubungan R. Contohnya -Input:x=1Output:1Explanation:set={1},reflexiverelationsonA*A:{{1}}Input:x=2Output:4Explanation:set={1,2},reflexiverelationsonA*





