 pembangunan bahagian belakang
pembangunan bahagian belakang
 C++
C++
 Apakah luas rombus terbesar yang mungkin boleh ditulis dalam segi empat tepat?
Apakah luas rombus terbesar yang mungkin boleh ditulis dalam segi empat tepat?
Apakah luas rombus terbesar yang mungkin boleh ditulis dalam segi empat tepat?

Rombus yang ditulis dalam segi empat tepat adalah tangen pada sisi segi empat tepat, jadi kita boleh membuat kesimpulan bahawa pepenjuru bagi rombus bertulis terbesar adalah sama dengan panjang dan lebar. daripada segi empat tepat itu.
Jika kita mempunyai panjang (l) dan lebar (b) segi empat tepat itu, panjang pepenjuru bagi rombus tertera terbesar ialah d1 = l dan d2 = b.
Luas rombus diberikan oleh formula berikut,
Area = (d1*d2)/2
Menggantikan nilai d1 dan d2, kita dapat:
Area = (l*b)/2
#include <stdio.h>
int main() {
float l = 16, b = 6;
float area = (l*b)/2;
printf("The area of rhombus inscribed in a rectangle of length %f and breadth %f is %f", l,b,area);
return 0;
}The area of rhombus inscribed in a rectangle of length 15 and breadth 12 is 90.
Atas ialah kandungan terperinci Apakah luas rombus terbesar yang mungkin boleh ditulis dalam segi empat tepat?. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

AI Hentai Generator
Menjana ai hentai secara percuma.

Artikel Panas

Alat panas

Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma

SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan

Hantar Studio 13.0.1
Persekitaran pembangunan bersepadu PHP yang berkuasa

Dreamweaver CS6
Alat pembangunan web visual

SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)

Topik panas
 1377
1377
 52
52
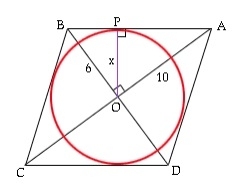 Berapakah luas bulatan yang tertulis dalam rombus?
Sep 05, 2023 am 08:25 AM
Berapakah luas bulatan yang tertulis dalam rombus?
Sep 05, 2023 am 08:25 AM
Bulatan bertulis rombus adalah tangen kepada empat sisi dan empat titik hujungnya. Sisi rombus adalah tangen kepada bulatan. Di sini, r ialah jejari yang ditemui menggunakan a dan pepenjuru nilai yang diberikan. Sekarang segitiga luas AOB = ½*OA*OB = ½*AB*r (kedua-duanya menggunakan formula ½*b*h). ½*a/2*b/2=½*(√(a2/4+b2/4))*ra*b/8=√(a2+b2)*r/4r=a*b/2√(a2 +b2) Luas bulatan = π*r*r=π*(a2*b2)/4(a2sokongan>+b2) Contoh pepenjuru rombus 5 dan 10. Kawasan ialah 15.700000 Contoh kod Demonstrasi masa nyata #include<stdio.h>intma
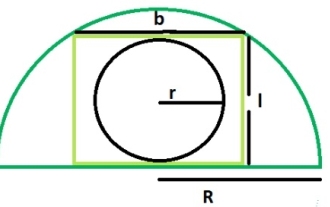 Apakah luas bulatan dalam segi empat tepat yang ditulis dalam separuh bulatan?
Sep 13, 2023 am 08:45 AM
Apakah luas bulatan dalam segi empat tepat yang ditulis dalam separuh bulatan?
Sep 13, 2023 am 08:45 AM
Bulatan yang ditulis dalam segi empat tepat adalah tangen pada sisi panjang segi empat tepat, iaitu panjangnya tangen dengan bulatan. Segi empat tepat yang ditulis dalam separuh bulatan menyentuh dua titik pada lengkok separuh bulatan itu. Lebar segi empat tepat adalah sama dengan diameter bulatan. Jika R ialah jejari separuh bulatan itu. Panjang segi empat tepat = √2R/2 Lebar segi empat tepat = R/√2 Jejari bulatan tersurat ialah r = b/2 = R/2√2 Dengan menggunakan formula ini kita boleh mengira segi empat tepat yang tertulis dalam separuh bulatan. Luas bulatan, luas = (π*r2)=π*R/8 Contoh Demonstrasi #include<stdio.h>intmain(){&
 Bagaimana untuk menggabungkan grafik selepas segi empat tepat CAD bertaburan
Feb 28, 2024 pm 12:10 PM
Bagaimana untuk menggabungkan grafik selepas segi empat tepat CAD bertaburan
Feb 28, 2024 pm 12:10 PM
Apabila menggunakan perisian CAD, kita sering menghadapi situasi di mana kita perlu menggabungkan semula objek segi empat tepat "berselerak" ke dalam satu grafik. Keperluan ini timbul dalam banyak bidang, seperti perancangan ruang, reka bentuk mekanikal dan lukisan seni bina. Untuk memenuhi permintaan ini, kita perlu memahami dan menguasai beberapa fungsi utama dalam perisian CAD. Seterusnya, editor laman web ini akan memperkenalkan anda secara terperinci bagaimana untuk menyelesaikan tugasan ini dalam persekitaran CAD Pengguna yang mempunyai keraguan boleh datang dan mengikuti artikel ini untuk belajar. Kaedah untuk menggabungkan segi empat tepat CAD ke dalam satu grafik selepas memecahkannya: 1. Buka perisian CAD2023, cipta segi empat tepat, dan kemudian masukkan arahan X dan ruang. Seperti yang ditunjukkan di bawah: 2. Pilih objek segi empat tepat dan jarakkannya. Anda boleh memecahkan objek. 3. Pilih semua baris terbuka
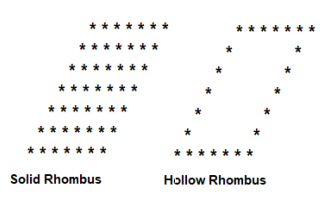 Tulis program dalam bahasa C untuk mencetak corak berlian pepejal dan berongga
Aug 29, 2023 am 09:33 AM
Tulis program dalam bahasa C untuk mencetak corak berlian pepejal dan berongga
Aug 29, 2023 am 09:33 AM
Penerangan Program Cetak corak pepejal dan rombus seperti ditunjukkan di bawah
 Bagaimana untuk mencetak bintang dalam corak berlian menggunakan bahasa C?
Sep 03, 2023 pm 02:41 PM
Bagaimana untuk mencetak bintang dalam corak berlian menggunakan bahasa C?
Sep 03, 2023 pm 02:41 PM
Di sini, untuk mencetak bintang dalam corak berlian, kami menggunakan bersarang untuk gelung. Logik yang kami gunakan untuk mencetak bintang dalam corak berlian adalah seperti berikut - //Forupperhalfofthediamondthelogicis:for(j=1;j<=rows;j++){ for(i=1;i<=rows-j;i++) printf( " "); untuk(i=1;i<=2*j-1;i++
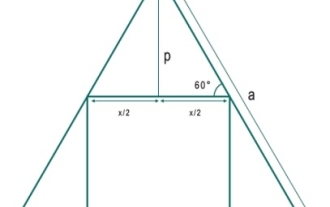 Apakah segi empat sama terbesar yang boleh ditulis dalam segi tiga sama?
Sep 22, 2023 pm 06:21 PM
Apakah segi empat sama terbesar yang boleh ditulis dalam segi tiga sama?
Sep 22, 2023 pm 06:21 PM
Di sini kita akan melihat luas segi empat sama terbesar yang boleh ditulis dalam segi tiga sama sisi. Panjang sisi segi tiga ialah 'a' dan panjang sisi segi empat itu ialah x. Panjang sisi 'a' bagi segi tiga ialah − jadi x ialah − Contoh #include<iostream>#include<cmath>usingnamespacestd;floatareaSquare(floata){//aissideoftriangle if(a<0)//ifaisnegative,thenthisisi
 Tulis program Java untuk mengira luas dan perimeter segi empat tepat menggunakan konsep kelas
Sep 03, 2023 am 11:37 AM
Tulis program Java untuk mengira luas dan perimeter segi empat tepat menggunakan konsep kelas
Sep 03, 2023 am 11:37 AM
Bahasa Java adalah salah satu bahasa pengaturcaraan berorientasikan objek yang paling biasa digunakan di dunia hari ini. Konsep kelas adalah salah satu ciri terpenting bahasa berorientasikan objek. Kelas adalah seperti pelan tindakan untuk objek. Sebagai contoh, apabila kita ingin membina rumah, kita mula-mula membuat blueprint rumah, dengan kata lain, kita membuat rancangan yang menunjukkan bagaimana kita akan membina rumah tersebut. Mengikut rancangan ini kita boleh membina banyak rumah. Begitu juga, menggunakan kelas, kita boleh mencipta banyak objek. Kelas ialah cetak biru untuk mencipta banyak objek, dengan objek ialah entiti dunia sebenar seperti kereta, basikal, pen, dsb. Kelas mempunyai ciri-ciri semua objek, dan objek mempunyai nilai ciri-ciri ini. Dalam artikel ini, kami akan menulis program Java untuk mencari perimeter dan muka segi empat tepat menggunakan konsep kelas
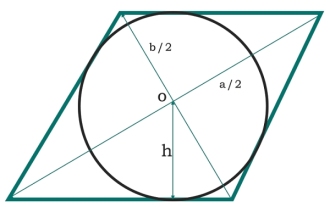 Dalam program C, apakah luas bulatan yang ditulis dalam rombus?
Sep 01, 2023 pm 09:29 PM
Dalam program C, apakah luas bulatan yang ditulis dalam rombus?
Sep 01, 2023 pm 09:29 PM
Di sini kita akan melihat luas bulatan yang tertulis dalam rombus. Diagonal bagi rombus ialah 'a' dan 'b' masing-masing. Jejari bulatan ialah h. Dua pepenjuru membentuk empat segi tiga sama. Setiap segi tiga ialah segi tiga tepat, jadi luasnya ialah - Setiap sisi rombus ialah hipotenus - Oleh itu, luas bulatan ialah - Contoh#include<iostream>#include<cmath>usingnamespacestd;floatarea(floata,floatb ) { jika(a<0||b<0)//ifthevaluesaren



