Apakah luas segi empat sama yang terbentuk dengan menggabungkan titik tengah berulang kali?

Luas segi empat sama adalah sama dengan hasil darab panjang sisi segi empat sama.

Kami menganggap rajah di mana titik tengah sisi setiap segi empat sama membentuk segi empat sama lain. Dan seterusnya sehingga bilangan petak tertentu.

Grafik ini menunjukkan segi empat sama yang terbentuk dengan menyambungkan titik tengah petak itu.

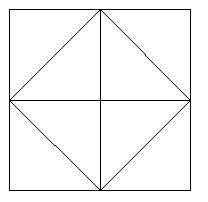
Untuk rajah ini, biarkan panjang sisinya ialah a,

Panjang sisi segi empat sama dalam ialah #🎜 🎜#

L2 = (a/2)<sup>2</sup> + (a/2)<sup>2</sup>
L2 = a<sup>2</sup>(1/4 + 1/4) = a<sup>2</sup>(1/2) = a<sup>2</sup>/2
L = a<sup>2</sup>/ (\sqrt{2}).

Luas petak 2 = L2 = a

2^/2.

Untuk petak seterusnya, luas petak 3 = a

2 ^/4

Mari kita ambil contoh, tge

Sekarang kita boleh membuat kesimpulan luas segi empat sama selanjar dari sini, # 🎜🎜#

a

2

, a²/2, a²##4, a^{##4, a#🎜 /8, …..}#🎜 🎜#Ini ialah jujukan geometri dengan nisbah sepunya ½, dengan a² ialah sebutan pertama.

Contoh

#include <stdio.h>
#include <math.h>
int main() {
   double L = 2, n = 10;
   double firstTerm = L * L;
   double ratio = 1 / 2.0;
   double are = firstTerm * (pow(ratio, 10)) ;
   printf("The area of %lfth square is %lf", n , sum);
   return 0;
}

Output

The area of 10th square is 0.003906

Atas ialah kandungan terperinci Apakah luas segi empat sama yang terbentuk dengan menggabungkan titik tengah berulang kali?. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!