Bilangan segi tiga sama kaki dalam pokok binari
Pohon binari ialah struktur data di mana setiap nod boleh mempunyai sehingga dua nod anak. Kanak-kanak ini dipanggil anak kiri dan anak kanan masing-masing. Katakan kita diberi perwakilan tatasusunan induk, anda perlu menggunakannya untuk mencipta pokok binari. Pokok binari mungkin mempunyai beberapa segi tiga sama kaki. Kita perlu mencari jumlah bilangan segi tiga sama kaki yang mungkin dalam pokok binari ini.
Dalam artikel ini, kami akan meneroka beberapa teknik untuk menyelesaikan masalah ini dalam C++.
Memahami masalah
Memberi anda susunan induk. Anda perlu mewakilinya dalam bentuk pokok binari supaya indeks tatasusunan membentuk nilai nod pokok dan nilai dalam tatasusunan memberikan nod induk indeks tertentu itu.
Sila ambil perhatian bahawa -1 sentiasa menjadi nod induk akar. Diberikan di bawah adalah tatasusunan dan perwakilan pokok binarinya.
Parent array = [0, -1, 3, 1, 1, 2, 2, 3, 4, 4]
Pokok binari -
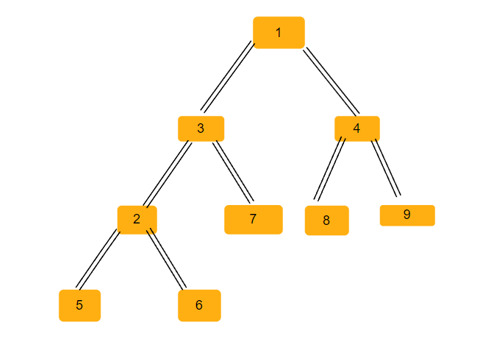
Dalam mana-mana pokok binari kita boleh mempunyai tiga jenis segi tiga sama kaki -
-
Segitiga Sama Kaki Kiri nod kanak-kanak. Nod anak boleh secara langsung atau tidak langsung. Dalam pokok di atas, kita mempunyai dua segi tiga sama kaki - (2, 6, 3), (3, 7, 1).
. Kanak-kanak boleh secara langsung atau tidak langsung. Dalam pokok di atas, kita hanya mempunyai satu segi tiga sama kaki (4, 1, 8). Balanced Isosceles Triangle − Dalam segi tiga ini, bucu yang membentuk tapak ialah nod anak kiri dan kanan nod bucu. Dalam pokok di atas, kita mempunyai lima segi tiga sama kaki (1, 3, 4), (3, 2, 7), (4, 8, 9), (2, 5, 6), (1, 2, 9)
-
Jadi, untuk pokok binari di atas, kami mempunyai sejumlah 8 segi tiga sama kaki. Perjalanan menggunakan carian depth-first Depth First Search (DFS) ialah kaedah merentasi semua nod pokok secara mendalam. Ia bermula pada nod akar, bergerak ke setiap cawangan, dan kemudian berundur. Pertama, kami menggunakan
DFS untuk merentasi setiap nod pokok binari dan menukarnya menjadi graf supaya setiap nod diwakili sebagai bersebelahan antara satu sama lain. Ini menjadikan perjalanan lebih mudah. Untuk setiap nod, kami menyemak sama ada ia mempunyai nod anak. Selepas menyemak, kami mengisihnya menggunakan fungsi sort(node[x].begin(), node[x].end()).
Seterusnya, kami menyemak sama ada nod semasa ialah pengganti kiri atau kanan nod induknya yang sepadan. Kami menggunakan fungsi DFS secara rekursif pada semua nod pokok binari.
Jika nod semasa mempunyai dua anak (langsung atau tidak langsung), kami menyemak kemungkinan segi tiga sama kaki wujud dengan mengira tepi di antara mereka. Kami akan mencari tepi di antara mereka melalui fungsi
grafyang diberikan dalam kod di bawah.
Akhir sekali, kami mengira jumlah bilangan segi tiga sama kaki dengan menjumlahkan semua segi tiga yang mungkin dalam kedudukan yang berbeza.
-
Contoh
Output#include <iostream> #include <vector> #include <algorithm> #include <cstring> using namespace std; #define MAX int(1e5) vector < int > * node; int right_down[MAX]; int right_up[MAX]; int left_down[MAX]; int left_up[MAX]; // DFS traversal over a node void DFS(int x, int * parent) { // Check if adjacent nodes are present for node x if (node[x].size() != 0) sort(node[x].begin(), node[x].end()); // Check whether the node has a parent node if (parent[x] != -1) { int indexOfParent = parent[x]; int childrenCount = node[indexOfParent].size(); if (childrenCount > 1) { int parentFirstChild = node[indexOfParent][0]; // Check if current node is left node of the parent if (x == parentFirstChild) { right_up[x] += right_up[indexOfParent] + 1; // Check if current node is right node of the parent } else { left_up[x] += left_up[indexOfParent] + 1; } } else { right_up[x] += right_up[indexOfParent] + 1; } } // Iterate over children of current node for (int i = 0; i < node[x].size(); ++i) { int y = node[x][i]; DFS(y, parent); // left child of current node if (i == 0) { left_down[x] += left_down[y] + 1; } // right child of current node else { right_down[x] += right_down[y] + 1; } } } int graph(int * parent, int N) { int rootNode; node = new vector < int > [N]; for (int i = 0; i < N; ++i) { if (parent[i] != -1) { node[parent[i]].push_back(i); } else { rootNode = i; } left_up[i] = 0; right_up[i] = 0; left_down[i] = 0; right_down[i] = 0; } return rootNode; } int main() { int N = 10; int parent[] = { 0, -1, 3, 1, 1, 2, 2, 3, 4, 4 }; int rootNode = graph(parent, N); DFS(rootNode, parent); int count = 0; // Counting the total isosceles triangles for (int i = 0; i < N; ++i) { count += min(right_down[i], right_up[i]); count += min(left_down[i], left_up[i]); count += min(left_down[i], right_down[i]); } cout << "Number of isosceles triangles in the binary tree are " << count; return 0; }Salin selepas log masukKesimpulanNumber of isosceles triangles in the binary tree are 8
Salin selepas log masuk -
Kami telah membincangkan cara mencari jumlah bilangan segi tiga sama sisi dalam pokok binari apabila diberikan tatasusunan induk. Kita boleh mencapai ini dengan menggunakan carian mendalam-pertama, yang membolehkan kita melintasi pokok binari.
Atas ialah kandungan terperinci Bilangan segi tiga sama kaki dalam pokok binari. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

AI Hentai Generator
Menjana ai hentai secara percuma.

Artikel Panas

Alat panas

Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma

SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan

Hantar Studio 13.0.1
Persekitaran pembangunan bersepadu PHP yang berkuasa

Dreamweaver CS6
Alat pembangunan web visual

SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)

Topik panas
 1377
1377
 52
52
 Kemas kini OpenOOD v1.5: perpustakaan kod pengesanan luar pengedaran yang komprehensif dan tepat serta platform ujian, menyokong kedudukan dalam talian dan ujian satu klik
Jul 03, 2023 pm 04:41 PM
Kemas kini OpenOOD v1.5: perpustakaan kod pengesanan luar pengedaran yang komprehensif dan tepat serta platform ujian, menyokong kedudukan dalam talian dan ujian satu klik
Jul 03, 2023 pm 04:41 PM
Pengesanan luar pengedaran (OOD) adalah penting untuk pengendalian sistem pintar dunia terbuka yang boleh dipercayai, tetapi kaedah pengesanan berorientasikan objek semasa mengalami "ketidakkonsistenan penilaian" (ketidakkonsistenan penilaian). Kerja sebelumnya OpenOODv1 menyatukan penilaian pengesanan OOD, tetapi masih mempunyai batasan dalam skalabilitas dan kebolehgunaan. Baru-baru ini, pasukan pembangunan sekali lagi mencadangkan OpenOODv1.5 Berbanding dengan versi sebelumnya, penilaian kaedah pengesanan OOD baharu telah dipertingkatkan dengan ketara dalam memastikan ketepatan, penyeragaman dan kemesraan pengguna. Kertas Imej: https://arxiv.org/abs/2306.09301OpenOODCodebase:htt
 Tingkatkan pengetahuan anda! Pembelajaran mesin dengan peraturan logik
Apr 01, 2023 pm 10:07 PM
Tingkatkan pengetahuan anda! Pembelajaran mesin dengan peraturan logik
Apr 01, 2023 pm 10:07 PM
Pada lengkung ingat-kepersisan, titik yang sama diplot dengan paksi yang berbeza. Amaran: Titik merah pertama di sebelah kiri (0% ingat, 100% ketepatan) sepadan dengan 0 peraturan. Titik kedua di sebelah kiri ialah peraturan pertama, dan seterusnya. Skope-rules menggunakan model pokok untuk menjana calon peraturan. Mula-mula bina beberapa pepohon keputusan dan pertimbangkan laluan dari nod akar ke nod dalaman atau nod daun sebagai calon peraturan. Peraturan calon ini kemudiannya ditapis oleh beberapa kriteria yang telah ditetapkan seperti ketepatan dan ingat semula. Hanya mereka yang mempunyai ketepatan dan ingatan di atas ambang mereka dikekalkan. Akhir sekali, penapisan persamaan digunakan untuk memilih peraturan dengan kepelbagaian yang mencukupi. Secara umum, Skope-rules digunakan untuk mengetahui punca setiap perkara
 Cetak paparan kiri pokok binari dalam bahasa C
Sep 03, 2023 pm 01:25 PM
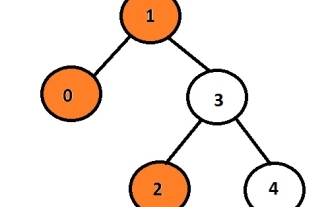
Cetak paparan kiri pokok binari dalam bahasa C
Sep 03, 2023 pm 01:25 PM
Tugasnya adalah untuk mencetak nod kiri pokok binari yang diberikan. Mula-mula, pengguna akan memasukkan data, dengan itu menjana pokok binari, dan kemudian mencetak pandangan kiri pokok yang terhasil. Setiap nod boleh mempunyai paling banyak 2 nod anak jadi atur cara ini mesti mengulangi hanya penunjuk kiri yang dikaitkan dengan nod jika penunjuk kiri tidak batal bermakna ia akan mempunyai beberapa data atau penunjuk yang dikaitkan dengannya jika tidak, ia akan dicetak dan dipaparkan sebagai anak kiri keluaran. ContohInput:10324Output:102Di sini, nod oren mewakili pandangan kiri pokok binari. Dalam graf yang diberikan, nod dengan data 1 adalah nod akar jadi ia akan dicetak dan bukannya pergi ke anak kiri ia akan mencetak 0 dan kemudian ia akan pergi ke 3 dan mencetak anak kirinya iaitu 2 . Kita boleh menggunakan kaedah rekursif untuk menyimpan tahap nod
 Penjelasan terperinci tentang struktur pokok binari di Jawa
Jun 16, 2023 am 08:58 AM
Penjelasan terperinci tentang struktur pokok binari di Jawa
Jun 16, 2023 am 08:58 AM
Pokok binari ialah struktur data biasa dalam sains komputer dan struktur data yang biasa digunakan dalam pengaturcaraan Java. Artikel ini akan memperkenalkan struktur pokok binari di Jawa secara terperinci. 1. Apakah pokok binari? Dalam sains komputer, pokok binari ialah struktur pokok di mana setiap nod mempunyai paling banyak dua nod anak. Antaranya, nod anak kiri lebih kecil daripada nod induk, dan nod anak kanan lebih besar daripada nod induk. Dalam pengaturcaraan Java, pokok binari biasanya digunakan untuk mewakili pengisihan, mencari dan meningkatkan kecekapan pertanyaan data. 2. Pelaksanaan pokok binari di Jawa Di Jawa, pokok binari
 Bagaimana untuk mencari bilangan parameter yang disediakan oleh runtime dalam Java?
Sep 23, 2023 pm 01:13 PM
Bagaimana untuk mencari bilangan parameter yang disediakan oleh runtime dalam Java?
Sep 23, 2023 pm 01:13 PM
Di Java, satu cara untuk menghantar parameter semasa runtime adalah dengan menggunakan baris arahan atau terminal. Apabila mendapatkan semula nilai ini untuk parameter baris arahan, kita mungkin perlu mencari bilangan parameter yang disediakan oleh pengguna pada masa jalan, yang boleh dicapai dengan bantuan atribut panjang. Artikel ini bertujuan untuk menerangkan proses lulus dan mendapatkan bilangan hujah yang dibekalkan pengguna dengan bantuan program sampel. Dapatkan bilangan argumen yang disediakan oleh pengguna pada masa jalankan Sebelum mencari bilangan argumen baris arahan, langkah pertama kami ialah mencipta program yang membolehkan pengguna menghantar argumen pada masa jalankan. Parameter string[] Semasa menulis atur cara Java, kita sering menemui kaedah main(). Apabila JVM memanggil kaedah ini, aplikasi Java mula melaksanakan. Ia digunakan dengan hujah yang dipanggil String[]args
 Perintah Linux: Bagaimana untuk menyemak bilangan proses telnet
Mar 01, 2024 am 11:39 AM
Perintah Linux: Bagaimana untuk menyemak bilangan proses telnet
Mar 01, 2024 am 11:39 AM
Perintah Linux adalah salah satu alat yang sangat diperlukan dalam kerja harian pentadbir sistem. Ia boleh membantu kami menyelesaikan pelbagai tugas pengurusan sistem. Dalam kerja operasi dan penyelenggaraan, kadangkala perlu menyemak bilangan proses tertentu dalam sistem untuk mengesan masalah dan membuat pelarasan dalam masa. Artikel ini akan memperkenalkan cara menggunakan arahan Linux untuk menyemak bilangan proses telnet, mari kita belajar bersama. Dalam sistem Linux, kita boleh menggunakan arahan ps digabungkan dengan arahan grep untuk melihat bilangan proses telnet. Pertama, kita perlu membuka terminal,
 Dalam bahasa C, cetak pandangan kanan pokok binari
Sep 16, 2023 pm 11:13 PM
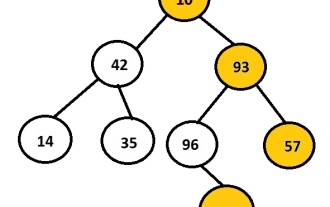
Dalam bahasa C, cetak pandangan kanan pokok binari
Sep 16, 2023 pm 11:13 PM
Tugasnya adalah untuk mencetak nod kanan pokok binari yang diberikan. Mula-mula pengguna akan memasukkan data untuk mencipta pokok binari dan kemudian mencetak pandangan kanan pokok yang terhasil. Imej di atas menunjukkan pepohon binari yang dicipta menggunakan nod 10, 42, 93, 14, 35, 96, 57 dan 88, dengan nod di sebelah kanan pepohon dipilih dan dipaparkan. Contohnya, 10, 93, 57, dan 88 ialah nod paling kanan bagi pokok binari. Contoh Input:1042931435965788Output:10935788 Setiap nod mempunyai dua penuding, penuding kiri dan penuding kanan. Menurut soalan ini, program hanya perlu melintasi nod yang betul. Oleh itu, anak kiri nod tidak perlu dipertimbangkan. Pandangan kanan menyimpan semua nod yang merupakan nod terakhir dalam hierarki mereka. Oleh itu, kita boleh
 Tulis kod menggunakan C++ untuk mencari bilangan subarray dengan nilai minimum dan maksimum yang sama
Aug 25, 2023 pm 11:33 PM
Tulis kod menggunakan C++ untuk mencari bilangan subarray dengan nilai minimum dan maksimum yang sama
Aug 25, 2023 pm 11:33 PM
Dalam artikel ini, kami akan menggunakan C++ untuk menyelesaikan masalah mencari bilangan subarray yang nilai maksimum dan minimumnya adalah sama. Berikut ialah contoh masalah −Input:array={2,3,6,6,2,4,4,4}Output:12Penjelasan:{2},{3},{6},{6}, {2 },{4},{4},{4},{6,6},{4,4},{4,4}dan{4,4,4}arethesubarraysyang boleh dibentuk denganmaksimumdanminimumelemensama.Input:array={3, 3, 1,5,




