 pembangunan bahagian belakang
pembangunan bahagian belakang
 C++
C++
 Jika tidak lebih daripada dua titik dalam satah adalah kolinear, berapakah bilangan segi tiga?
Jika tidak lebih daripada dua titik dalam satah adalah kolinear, berapakah bilangan segi tiga?
Jika tidak lebih daripada dua titik dalam satah adalah kolinear, berapakah bilangan segi tiga?
Mari kita lihat cara mengira bilangan segi tiga pada satah diberi n mata, dan hadkan bilangan titik kolinear kepada tidak lebih daripada dua.
Mengira bilangan segi tiga dalam satah dengan tidak lebih daripada dua titik kolinear ialah masalah biasa dalam geometri pengiraan, yang digunakan dalam grafik komputer, pemprosesan imej dan bidang sains komputer yang lain.
Sebagai contoh, apabila mencipta imej 2D daripada pemandangan 3D dalam grafik 3D, masalah mungkin timbul untuk mengira segi tiga dalam satah yang tidak lebih daripada dua titik kolinear. Dalam kes ini, proses pengiraan segi tiga boleh digunakan untuk menentukan bilangan segi tiga yang terdapat dalam imej 2D akhir selepas menayangkan pemandangan 3D pada satah. Ini membolehkan anda menentukan kerumitan adegan dan meningkatkan kelajuan pemaparan.
Dalam pemprosesan imej, kita mungkin ingin mengira bilangan objek atau bentuk unik dalam imej, soalan ini berguna. Dalam kes ini, kita boleh mewakili imej sebagai koleksi mata pada satah, dan kemudian kita boleh mengira bilangan segi tiga yang boleh dibuat antara titik ini dengan menggunakan teknik mengira segi tiga. Kita boleh menentukan anggaran bilangan item atau bentuk yang berbeza dalam imej dengan mengira bilangan segi tiga yang terbentuk.
Arahan
Mari kita memahami masalah ini melalui beberapa contoh dan cuba menyelesaikannya.
Tujuannya adalah untuk menentukan berapa banyak segitiga yang terbentuk pada satah dengan n titik supaya tidak lebih daripada dua titik adalah kolinear.
Contoh -
Anggap N ialah bilangan mata pada pesawat.
N = 3
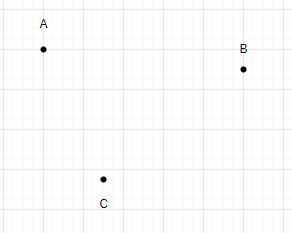
Menggunakan mata ini kita hanya boleh melukis segitiga.
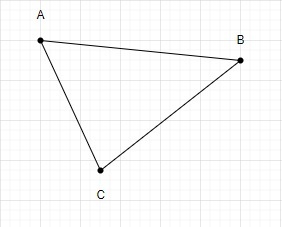
Jadi jumlah bilangan segi tiga yang terbentuk menggunakan 3 titik ialah 1.
Misalkan N = 4
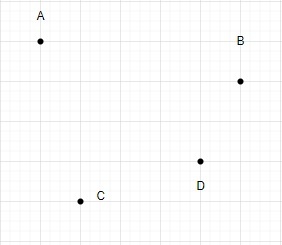
Mari lukis segitiga menggunakan empat titik ini.
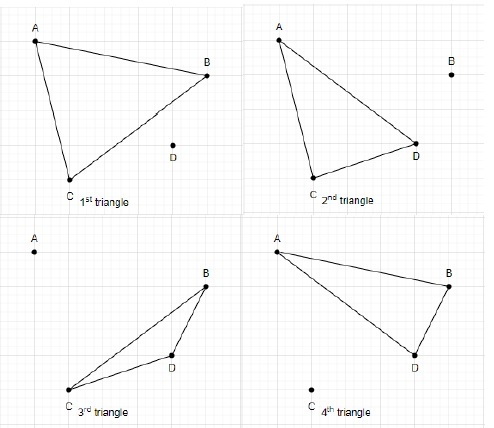
Jumlah bilangan segi tiga yang terbentuk menggunakan 4 titik ialah 4.
Mari kita lihat beberapa matematik yang terlibat dalam pengiraan bilangan segi tiga. Ini boleh diperoleh menggunakan pilih atur dan kombinasi. Untuk membina segitiga, anda memerlukan 3 mata daripada jumlah pada satu masa.
Oleh itu, jika satah mengandungi n titik dan tidak lebih daripada dua daripadanya adalah kolinear, maka bilangan segi tiga dalam satah itu diberikan oleh formula berikut.
$$mathrm{n_{C_{3}}:=:frac{n(n-1):(n-2)}{6}}$$
Kaedah
Atur cara mencari bilangan segi tiga dalam satah jika tidak lebih daripada dua titik adalah kolinear, menggunakan algoritma berikut.
Ambil bilangan mata pada satah sebagai input dan hadkannya kepada tidak lebih daripada dua titik kolinear.
Kira jumlah bilangan segi tiga menggunakan formula di atas.
Cetak jumlah bilangan segi tiga sebagai output.
Contoh
Aturcara C++ untuk mengira bilangan segi tiga dalam satah jika tidak lebih daripada dua titik adalah kolinear.
#include <iostream>
using namespace std;
int main() {
int number_of_points = 4;
int number_of_triangle;
number_of_triangle = number_of_points * (number_of_points - 1) * (number_of_points - 2) / 6;
cout << "Total number of triangles formed using " << number_of_points<< " points = " << number_of_triangle << endl;
return 0;
}
Output
Total number of triangles formed using 4 points = 4
Kerumitan
Kerumitan Masa: O(1) kerana kod ini melakukan bilangan pengiraan tetap tanpa mengira saiz input.
Kerumitan Ruang: O(1) kerana kod menggunakan bilangan pembolehubah tetap untuk menyimpan nilai input dan hasil tanpa mengira saiz input.
Kesimpulan
Dalam artikel ini, kami cuba menerangkan kaedah untuk mencari jumlah bilangan segitiga yang mungkin dengan n titik yang diberikan, dengan kekangan bahawa tiada dua titik adalah kolinear. Saya harap artikel ini membantu anda mempelajari konsep ini dengan lebih baik.
Atas ialah kandungan terperinci Jika tidak lebih daripada dua titik dalam satah adalah kolinear, berapakah bilangan segi tiga?. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

AI Hentai Generator
Menjana ai hentai secara percuma.

Artikel Panas

Alat panas

Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma

SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan

Hantar Studio 13.0.1
Persekitaran pembangunan bersepadu PHP yang berkuasa

Dreamweaver CS6
Alat pembangunan web visual

SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)

Topik panas
 1377
1377
 52
52
 Program Java untuk mengira luas segi tiga menggunakan penentu
Aug 31, 2023 am 10:17 AM
Program Java untuk mengira luas segi tiga menggunakan penentu
Aug 31, 2023 am 10:17 AM
Pengenalan Program Java untuk mengira luas segi tiga menggunakan penentu adalah program ringkas dan cekap yang boleh mengira luas segitiga diberi koordinat tiga bucu. Program ini berguna untuk sesiapa sahaja yang belajar atau bekerja dengan geometri, kerana ia menunjukkan cara menggunakan pengiraan aritmetik dan algebra asas dalam Java, serta cara menggunakan kelas Pengimbas untuk membaca input pengguna. Program ini menggesa pengguna untuk koordinat tiga titik segi tiga, yang kemudiannya dibaca dan digunakan untuk mengira penentu matriks koordinat. Gunakan nilai mutlak penentu untuk memastikan kawasan sentiasa positif, kemudian gunakan formula untuk mengira luas segi tiga dan memaparkannya kepada pengguna. Program ini boleh diubah suai dengan mudah untuk menerima input dalam format yang berbeza atau untuk melakukan pengiraan tambahan, menjadikannya alat serba boleh untuk pengiraan geometri. pangkat penentu
 Ditulis dalam C++, cari bilangan segi tiga yang dibentuk oleh set titik pada tiga garis
Sep 09, 2023 am 09:53 AM
Ditulis dalam C++, cari bilangan segi tiga yang dibentuk oleh set titik pada tiga garis
Sep 09, 2023 am 09:53 AM
Sekarang kita mendapat beberapa mata dalam 3 baris sebagai contoh, kita perlu mengetahui berapa banyak segi tiga titik ini boleh membentuk Input:m=3,n=4,k=5Output:205Input:m=2,n=2, k =1Output:10 Kami akan menggunakan beberapa matematik gabungan untuk menyelesaikan masalah ini dan merumuskan beberapa formula untuk menyelesaikan masalah ini. Kaedah untuk mencari penyelesaian Dalam kaedah ini kita akan merangka formula: menggunakan kombinatorik kepada situasi semasa, formula ini akan memberikan kita hasilnya. Kod C++ untuk kaedah di atas Ini ialah sintaks C++ yang boleh kita gunakan sebagai input untuk menyelesaikan masalah yang diberikan - contoh #include<bits/stdc++.h>#define
 Bagaimana untuk menaip titik '丶' menggunakan papan kekunci?
Feb 15, 2024 pm 01:51 PM
Bagaimana untuk menaip titik '丶' menggunakan papan kekunci?
Feb 15, 2024 pm 01:51 PM
Apabila menaip pada papan kekunci, ramai pengguna ingin tahu bagaimana untuk menaip titik "丶" pada papan kekunci? Jadi mari kita lihat kaedah yang editor bawa kepada anda tentang cara menaip simbol "丶" ini pada papan kekunci. 1. Klik "丶" dan taip terus pada papan kekunci [dian]. Anda akan melihat tanda baca [丶] pada bar pilihan. 2. Simbol khas Dalam kaedah input Sogou Pinyin, apabila bertukar kepada mod Cina, menekan kekunci v akan menyebabkan beberapa simbol khas muncul. Simbol ini termasuk nombor (cth: v123), tarikh (cth: v2013/1/1), pengiraan (cth: v1+1) dan fungsi (cth: v2~3). Simbol-simbol ini memudahkan untuk memasukkan pelbagai maklumat yang berbeza. 2. Kemudian tekan kekunci nombor sekali lagi, sebarang nombor dari 0 hingga 9 boleh digunakan
 Bagaimana untuk menyemak sama ada tiga mata adalah kolinear di Jawa?
Sep 05, 2023 pm 06:41 PM
Bagaimana untuk menyemak sama ada tiga mata adalah kolinear di Jawa?
Sep 05, 2023 pm 06:41 PM
Jika tiga titik terletak pada garis lurus, ia dikatakan kolinear. Jika titik tidak berada pada garis lurus yang sama, ia bukan kolinear. Ini bermakna jika tiga titik (x1,y1), (x2,y2), (x3,y3) berada pada garis lurus yang sama, ia adalah kolinear. Antaranya, x1, y1, x2, y2, x3, y3 ialah titik pada paksi-x dan paksi-y, (x1, y1), (x2, y2), (x3, y3) ialah koordinat. Secara matematik, terdapat dua cara untuk menentukan sama ada tiga titik adalah kolinear. Cari luas segi tiga dengan menggunakan titik Jika luas segitiga adalah sifar, maka tiga titik adalah kolinear. Formulatofindareaoftriangle=0.5*[x1*(y2-y3)+x2*
 Pengaturcaraan dalam C++, cari bilangan laluan dari satu titik ke titik lain dalam grid
Aug 29, 2023 pm 10:25 PM
Pengaturcaraan dalam C++, cari bilangan laluan dari satu titik ke titik lain dalam grid
Aug 29, 2023 pm 10:25 PM
Dalam artikel ini, kita diberikan masalah di mana kita perlu mencari jumlah bilangan laluan dari titik A ke titik B, di mana A dan B adalah titik tetap, iaitu A ialah titik sudut kiri atas dalam grid dan B ialah Titik Bawah. titik sudut kanan, contohnya −Input:N=5Output:252Input:N=4Output:70Input:N=3Output:20 Dalam masalah yang diberikan, kita boleh merumuskan jawapan dan memperoleh hasilnya melalui pemerhatian mudah. Kaedah mencari penyelesaian Dalam kaedah ini kita memperoleh formula dengan memerhatikan bahawa apabila melintasi grid dari A ke B kita perlu pergi ke kanan n kali dan ke bawah n kali yang bermaksud kita perlu mencari semua kombinasi laluan yang mungkin, jadi kita mendapat
 Bagaimana untuk mencari ketinggian minimum segi tiga yang diberikan tapak dan kawasan di Jawa?
Aug 26, 2023 pm 10:25 PM
Bagaimana untuk mencari ketinggian minimum segi tiga yang diberikan tapak dan kawasan di Jawa?
Aug 26, 2023 pm 10:25 PM
Kami mempunyai kawasan 'a' dan tapak 'b' bagi segi tiga. Mengikut pernyataan masalah, kita perlu mencari ketinggian minimum 'h' menggunakan bahasa pengaturcaraan Java. Seperti yang kita ketahui, apabila tapak dan tinggi diberi, luas segi tiga ialah −$$\mathrm{luas\:=\:\frac{1}{2}\:*\:base\:*\ : Height}$$ Dengan menggunakan formula di atas, kita boleh mendapatkan ketinggian dari -height=(2*luas)/base dan kemudian dengan menggunakan kaedah ceil() terbina dalam, kita boleh mendapatkan ketinggian minimum. Tunjukkan kepada anda beberapa contoh untuk menunjukkan kepada anda terjemahan Bahasa Cina bagi Contoh-1: Contoh-1 Katakan kawasan yang diberi = 12 dan asas = 6 dan kemudian gunakan formula
 Program C++ untuk mencetak jadual pendaraban dalam bentuk segi tiga
Sep 15, 2023 pm 01:21 PM
Program C++ untuk mencetak jadual pendaraban dalam bentuk segi tiga
Sep 15, 2023 pm 01:21 PM
Untuk mengingati beberapa hasil pendaraban asas dalam bentuk jadual atau grafik, gunakan jadual pendaraban. Artikel ini akan memperkenalkan cara menggunakan C++ untuk menjana jadual pendaraban yang kelihatan seperti segi tiga tepat. Notasi segi tiga berkesan dalam beberapa kes di mana sejumlah besar hasil boleh dihafal dengan mudah. Dalam format ini, jadual dipaparkan baris demi baris dan lajur demi lajur, dengan setiap baris hanya mengandungi entri yang mengisi lajur tersebut. Untuk menyelesaikan masalah ini, kita memerlukan pernyataan gelung asas dalam C++. Untuk memaparkan nombor dalam bentuk segi tiga, kita memerlukan gelung bersarang untuk mencetak setiap baris satu demi satu. Kita akan lihat bagaimana untuk menyelesaikan masalah ini. Mari kita lihat algoritma dan pelaksanaan untuk pemahaman yang lebih baik. Algoritma mengambil bilangan baris jadual pendaraban yang kita mahu, katakan n. Untuk i dari 1 hingga n, lakukan perkara berikut. Untuk j antara 1 hingga i,
 Bilangan maksimum garis lurus berbeza melalui satu titik dalam C
Aug 26, 2023 am 10:25 AM
Bilangan maksimum garis lurus berbeza melalui satu titik dalam C
Aug 26, 2023 am 10:25 AM
Kami mendapat nombor N untuk setiap baris dan koordinat dua titik (x1,y1) dan (x2,y2). Matlamatnya adalah untuk mencari bilangan maksimum garis lurus daripada garis lurus yang diberikan yang boleh melalui satu titik supaya tiada dua garis lurus menutup satu sama lain dan tiada putaran dilakukan. Kami akan mewakili garis lurus sebagai (pasangan)m,c) dengan y=mx+c dan m ialah cerun m=y2-y1/x2-x1 Diberi c1!=c2, garisan dengan m yang sama adalah selari. Kami akan mengira cerun yang berbeza dalam meter. Untuk garis menegak, jika x1=x2, maka cerun=INT_MAX, jika tidak m. Mari kita fahami dengan contoh. Baris Input1(x1,y1)=(4,10)(x2,y2)=(2,2)Baris2(x1,y1)=(2



