Program C++ untuk mencari komponen skor maksimum yang boleh dikurangkan daripada graf

Andaikan terdapat graf berwajaran tidak berarah dengan n bucu dan m tepi. Skor graf ditakrifkan sebagai jumlah pemberat semua tepi dalam graf. Pemberat tepi boleh menjadi negatif, dan jika ia dialih keluar, skor graf akan meningkat. Apa yang perlu kita lakukan ialah meminimumkan skor graf dengan mengalihkan tepi dalam graf sambil mengekalkan ketersambungan graf. Kita perlu mencari markah maksimum yang boleh dikurangkan.

Graf diberikan dalam bentuk 'tepi' tatasusunan, di mana setiap elemen adalah dalam bentuk {berat, {bucu1, bucu2}}.

Jadi jika input ialah n = 5, m = 6, tepi = {{2, {1, 2}}, {2, {1, 3}}, {1, {2, 3}}, {3 , {2, 4}}, {2, {2, 5}}, {1, {3, 5}}}, maka outputnya ialah 4.

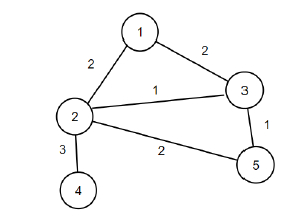
Jika kita mengalih keluar tepi (1, 2) dan (2, 5) daripada graf, jumlah pengurangan markah ialah 4 dan graf masih kekal bersambung.

Untuk menyelesaikan masalah ini kami akan mengikuti langkah berikut:

cnum := 0
Define an array par of size: 100.
Define an array dim of size: 100.
Define a function make(), this will take v,
   par[v] := v
   dim[v] := 1
Define a function find(), this will take v,
   if par[v] is same as v, then:
      return v
   return par[v] = find(par[v])
Define a function unify(), this will take a, b,
a := find(a)
b := find(b)
if a is not equal to b, then:
   (decrease cnum by 1)
   if dim[a] > dim[b], then:
      swap values of (a, b)
   par[a] := b
   dim[b] := dim[b] + dim[a]
cnum := n
sort the array edges based on edge weights
for initialize i := 1, when i <= n, update (increase i by 1), do:
   make(i)
res := 0
for each edge in edges, do:
   a := first vertex of edge
   b := second vertex of edge
   weight := weight of edge
   if find(a) is same as find(b), then:
      if weight >= 0, then:
         res := res + 1 * weight
      Ignore following part, skip to the next iteration
   if cnum is same as 1, then:
      if weight >= 0, then:
         res := res + 1 * weight
   Otherwise
      unify(a, b)
return res

Contoh

Mari lihat pelaksanaan berikut untuk pemahaman yang lebih baik -

#include <bits/stdc++.h>
using namespace std;

int cnum = 0;
int par[100];
int dim[100];

void make(int v){
   par[v] = v;
   dim[v] = 1;
}
int find(int v){
   if(par[v] == v)
   return v;
   return par[v] = find(par[v]);
}
void unify(int a, int b){
   a = find(a); b = find(b);
   if(a != b){
      cnum--; if(dim[a] > dim[b]){
         swap(a, b);
      }
      par[a] = b; dim[b] += dim[a];
   }
}
int solve(int n, int m, vector <pair <int, pair<int,int>>> edges){
   cnum = n;
   sort(edges.begin(), edges.end());
   for(int i = 1; i <= n; i++)
      make(i);
   int res = 0;
   for(auto &edge : edges){
      int a = edge.second.first;
      int b = edge.second.second;
      int weight = edge.first;
      if(find(a) == find(b)) {
         if(weight >= 0) 
            res += 1 * weight;
         continue;
      }
      if(cnum == 1){
         if(weight >= 0)
            res += 1 * weight;
      } else{
         unify(a, b);
      }
   }
   return res;
}
int main() {
   int n = 5, m = 6;
   vector <pair<int, pair<int,int>>> edges = {{2, {1, 2}}, {2, {1, 3}}, {1, {2, 3}}, {3, {2, 4}}, {2, {2, 5}}, {1, {3, 5}}};
   cout<< solve(n, m, edges);
   return 0;
}

Input

5, 6, {{2, {1, 2}}, {2, {1, 3}}, {1, {2, 3}}, {3, {2, 4}}, {2, {2, 5}}, {1, {3, 5}}}

Output

rreee

Atas ialah kandungan terperinci Program C++ untuk mencari komponen skor maksimum yang boleh dikurangkan daripada graf. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!