 pembangunan bahagian belakang
pembangunan bahagian belakang
 C++
C++
 Ungkapkan faktorial n sebagai hasil tambah nombor berturut-turut
Ungkapkan faktorial n sebagai hasil tambah nombor berturut-turut
Ungkapkan faktorial n sebagai hasil tambah nombor berturut-turut

Kita akan membincangkan dua kaedah untuk mengetahui cara menyatakan pemfaktoran nombor sebagai hasil tambah nombor berturut-turut. Kaedah pertama ialah kaedah langsung dan mudah, manakala dalam kaedah lain kita menggunakan konsep janjang aritmetik untuk menjadikannya kurang kompleks dari segi masa dan ruang yang diduduki.
Pernyataan Masalah
Diberi nombor, kita perlu mencari cara untuk menyatakan pemfaktoran nombor itu sebagai hasil tambah nombor asli yang berturutan.
Ini melibatkan dua fungsi berbeza -
Cari faktorial bagi suatu nombor.
Cari bilangan cara nombor boleh dinyatakan sebagai hasil tambah nombor asli berturut-turut.
Contoh 1
Given : Number = 3 Result: 1
Kita semua tahu bahawa faktorial bagi 3 ialah 6, yang boleh ditulis sebagai 1+2+3, jadi jawapan kita ialah: 1 cara.
Contoh 2
Given: Number = 4 Result: 1
Kita semua tahu bahawa faktorial bagi 4 ialah 24, yang boleh ditulis sebagai 7+8+9, jadi jawapan kita ialah: 1 cara.
Kaedah 1
Ini adalah kaedah mudah di mana kita mula-mula mencari faktorial nombor dan kemudian mengira bilangan cara ia boleh dinyatakan sebagai hasil tambah nombor asli berturut-turut. Kaedahnya ialah untuk menyatakan faktorial sebagai satu siri aritmetik panjang len+1 sebagai -
Factorial of Number = p + (p+1) + (p+2) + … + (p+len) So, p = (Number- len*(len+1)/2)/(len+1) We will check for the values of len from 1 to len*(len+1)/2<Number
Apabila kami mendapat len sebagai integer positif, kami menganggapnya sebagai penyelesaian.
Contoh
Dalam contoh di bawah, kami cuba mencari bilangan cara untuk menyatakan pemfaktoran nombor sebagai hasil tambah nombor berturut-turut.
#include <bits/stdc++.h>
using namespace std;
// code for obtaining number of possible solutions
long int Number_of_solutions(long int NUMBER){
long int counter = 0;
for (long int len = 1; len * (len + 1) < 2 * NUMBER; len++) {
double p = (1.0 * NUMBER - (len * (len + 1)) / 2) / (len + 1);
if (p - (int)p == 0.0)
counter++;
}
return counter;
}
// main program goes here
int main(){
long int NUMBER = 15;
cout << "Number of ways to write 15 as a sum of consecutive numbers: ";
cout << Number_of_solutions(NUMBER) << endl;
NUMBER = 10;
cout << "Number of ways to write 10 as a sum of consecutive numbers: ";
cout << Number_of_solutions(NUMBER) << endl;
return 0;
}
Output
Apabila anda menjalankan program C++ di atas, ia akan menghasilkan output berikut -
Number of ways to write 15 as a sum of consecutive numbers: 3 Number of ways to write 10 as a sum of consecutive numbers: 1
Kaedah 2: Kaedah pengoptimuman
Ini adalah pendekatan yang lebih baik; pendekatan yang kami lihat di atas menyebabkan limpahan.
Jumlah nombor berturut-turut len bermula dari nombor p boleh ditulis sebagai -
sum = (p+1) + (p+2) + (p+3) … + (p+len) Hence, sum = (len*(len + 2*p + 1))/2
Sebab sum juga sama dengan Nombor!.
Kita boleh menulis
2*Number! = (len*(len + 2*p + 1))
Di sini, daripada mengira semua pasangan (len, p), kita akan mengira semua pasangan (len, (len + 2*p + 1)). Ini bermakna kita akan mengira semua pf yang dipesan (A, B) dengan AB=2*Nombor! Dan A< B 且 A 和 B 的奇偶性不同,这意味着如果 len 是奇数,则 (len + 2*p + 1) 是偶数,如果 len 是偶数,则 (len + 2*p + 1) 是奇数。
Ini bermakna kami sedang mencari pembahagi ganjil 2*Nombor! Ini juga pembahagi ganjil Nombor!
Kira bilangan pembahagi! , kita perlu mengira kuasa nombor perdana dalam pemfaktoran, bilangan pembahagi ialah (f1 + 1)*(f2 + 1)* … *(fn + 1).
Kami akan menggunakan formula Legendre untuk mengira kuasa tertinggi nombor perdana dalam pemfaktoran nombor.
Contoh
Kod untuk pendekatan ini diberikan di bawah -
#include <bits/stdc++.h>
using namespace std;
#define maximum 5002
vector<int> v;
void sieve(){
bool Is_the_number_prime[maximum];
memset (Is_the_number_prime, true, sizeof(Is_the_number_prime) );
for (int prime = 2; prime * prime < maximum; prime++) {
if (Is_the_number_prime[prime] == true) {
for (int iterator = prime * 2; iterator < maximum; iterator += prime)
Is_the_number_prime[iterator] = false;
}
}
for (int prime = 2; prime < maximum; prime++)
if (Is_the_number_prime[prime])
v.push_back(prime);
}
long long int calculate_largest_power(long long int a, long long int b){
long long int c = 0;
long long int x = b;
while (a >= x) {
c += (a / x);
x *= b;
}
return c;
}
long long int modular_mult(long long int a,
long long int b,
long long int m){
long long int result = 0;
a = a % m;
while (b > 0) {
if (b % 2 == 1)
result = (result + a) % m;
a = (a * 2) % m;
b /= 2;
}
return result % m;
}
long long int no_of_ways(long long int n,
long long int m){
long long int answer = 1;
for (int iterator = 1; iterator < v.size(); iterator++) {
long long int powers = calculate_largest_power(n, v[iterator]);
if (powers == 0)
break;
answer = modular_mult(answer, powers + 1, m)%m;
}
if (((answer - 1) % m) < 0)
return (answer - 1 + m) ;
else
return (answer - 1) ;
}
int main(){
sieve();
long long int n = 4, m = 7;
cout << "Number of solutions after performing modulo with 7 is " <<no_of_ways(n, m);
return 0;
}
Output
Apabila program C++ di atas dijalankan, ia akan menghasilkan output berikut -
Number of solutions after performing modulo with 7 is 1.
Kesimpulan
Dalam artikel ini, kami membincangkan dua cara berbeza untuk mengetahui faktorial nombor sebagai hasil tambah nombor asli berturut-turut.
Atas ialah kandungan terperinci Ungkapkan faktorial n sebagai hasil tambah nombor berturut-turut. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

AI Hentai Generator
Menjana ai hentai secara percuma.

Artikel Panas

Alat panas

Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma

SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan

Hantar Studio 13.0.1
Persekitaran pembangunan bersepadu PHP yang berkuasa

Dreamweaver CS6
Alat pembangunan web visual

SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)

Topik panas
 1376
1376
 52
52
 Jumlah tuple mutlak dalam Python
Sep 12, 2023 pm 07:37 PM
Jumlah tuple mutlak dalam Python
Sep 12, 2023 pm 07:37 PM
Dalam Python, tupel ialah jujukan tidak berubah yang boleh menyimpan berbilang elemen daripada jenis yang berbeza. Ia sering digunakan untuk mewakili koleksi nilai yang berkaitan. Penjumlahan tupel melibatkan penambahan elemen sepadan dua atau lebih tupel untuk menghasilkan tupel baharu. Walau bagaimanapun, dalam sesetengah senario, mungkin perlu untuk mengira jumlah mutlak unsur dan bukannya jumlah tradisional. Dalam catatan blog ini, kami akan meneroka cara melakukan jumlah tuple mutlak dalam Python. Jumlah Tuple Tradisional Sebelum kita mendalami jumlah tupel mutlak, mari kita fahami terlebih dahulu cara melakukan jumlah tuple tradisional. Memandangkan dua tupel yang sama panjang, kita boleh menggunakan gelung Python mudah atau pemahaman senarai untuk mengira jumlah elemen yang sepadan −deftuple_sum(t1,t2):
 Adakah anda tahu cara menjumlahkan jadual Word?
Mar 21, 2024 pm 01:10 PM
Adakah anda tahu cara menjumlahkan jadual Word?
Mar 21, 2024 pm 01:10 PM
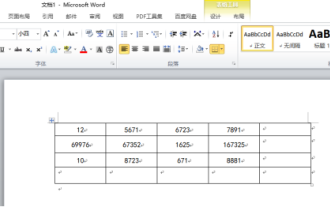
Kadangkala, kita sering menghadapi masalah mengira dalam jadual Word Secara amnya, apabila menghadapi masalah seperti itu, kebanyakan pelajar akan menyalin jadual Word ke Excel untuk pengiraan secara senyap. Adakah terdapat cara cepat untuk mengiranya? Sudah tentu ada, sebenarnya jumlahnya juga boleh dikira dalam Word. Jadi, adakah anda tahu bagaimana untuk melakukannya? Hari ini, mari kita lihat bersama-sama! Tanpa berlengah lagi, rakan-rakan yang memerlukan perlu segera mengumpulnya! Butiran langkah: 1. Mula-mula, kita buka perisian Word pada komputer dan buka dokumen yang perlu diproses. (Seperti yang ditunjukkan dalam gambar) 2. Seterusnya, kami meletakkan kursor pada sel di mana nilai yang dijumlahkan terletak (seperti yang ditunjukkan dalam gambar kemudian, kami klik [Bar Menu);
 Cari hasil tambah jujukan aritmetik bagi tanda berperingkat
Sep 16, 2023 pm 05:01 PM
Cari hasil tambah jujukan aritmetik bagi tanda berperingkat
Sep 16, 2023 pm 05:01 PM
Janjang aritmetik (AP) ialah jujukan nombor di mana perbezaan antara dua sebutan berturut-turut adalah sama. Perbezaan dikira dengan menolak sebutan kedua daripada sebutan pertama. Mari kita fahami AP dengan urutan contoh, 5,7,9,11,13,15,... Toleransi (d) bagi siri aritmetik ini ialah 2. Ini bermakna setiap elemen berikutnya berbeza daripada elemen sebelumnya sebanyak 2. Item pertama (a) dalam urutan ini ialah 5. Formula umum untuk mencari sebutan ke-n ialah a{n}=a+(n-1)(d) Dalam masalah ini kita diberi AP dan kita perlu mencari jumlah siri petak bertanda selang seli, sirinya akan Seperti yang ditunjukkan di bawah, a12-a22+a32-a42+a52+... Mari kita ambil contoh untuk pemahaman yang lebih jelas&
 Cari jumlah elemen dalam tatasusunan menggunakan fungsi array_sum() dalam PHP
Nov 18, 2023 am 11:20 AM
Cari jumlah elemen dalam tatasusunan menggunakan fungsi array_sum() dalam PHP
Nov 18, 2023 am 11:20 AM
Tajuk: Cari jumlah elemen tatasusunan menggunakan fungsi array_sum() dalam PHP PHP ialah bahasa skrip bahagian pelayan yang digunakan secara meluas yang menyediakan banyak fungsi terbina dalam yang memudahkan proses pembangunan dan meningkatkan kecekapan. Antaranya, fungsi array_sum() ialah fungsi yang sangat praktikal yang boleh digunakan untuk mengira jumlah elemen dalam tatasusunan. Dalam artikel ini, kita akan belajar cara menggunakan fungsi array_sum() dan memberikan contoh kod tertentu. Pertama, kita perlu memahami penggunaan fungsi array_sum().
 Bagaimana untuk menjumlahkan jumlah dalam excel secara automatik
Mar 20, 2024 pm 12:20 PM
Bagaimana untuk menjumlahkan jumlah dalam excel secara automatik
Mar 20, 2024 pm 12:20 PM
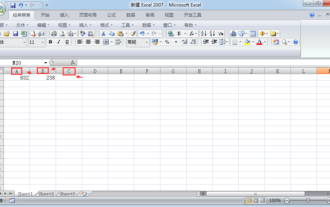
Bagi pengguna yang sering menggunakan jadual excel, fungsi jumlah automatik adalah operasi yang sangat mudah, dan ia secara automatik boleh menjumlahkan kepada beberapa tempat perpuluhan mengikut keperluan kita, yang jauh lebih mudah daripada menekan kalkulator secara manual. Untuk pengguna pemula, anda perlu belajar cara menjumlahkan jumlah secara automatik dalam Excel dari awal Mari kita lihat langkah-langkah: Jumlah automatik Excel: Pertama, kita perlu menambah nombor dalam sel A1 dan B1, dan Paparkan keputusan dalam sel. C1. Untuk melakukan ini, mula-mula masukkan nombor yang anda mahu tambah dalam sel A1 dan B1. Seterusnya, pilih sel C1 dan masukkan formula berikut: `=A1+B1` Selepas menekan kekunci Enter, sel C1 akan memaparkan jumlah nombor dalam sel A1 dan B1.
 Bagaimana untuk menggunakan fungsi tatasusunan bahasa Go untuk menjumlahkan dan mengembalikan hasilnya?
Jul 31, 2023 pm 02:25 PM
Bagaimana untuk menggunakan fungsi tatasusunan bahasa Go untuk menjumlahkan dan mengembalikan hasilnya?
Jul 31, 2023 pm 02:25 PM
Bagaimana untuk menggunakan fungsi tatasusunan bahasa Go untuk menjumlahkan dan mengembalikan hasilnya? Bahasa Go menyediakan banyak fungsi operasi tatasusunan, termasuk fungsi untuk mencari jumlah elemen tatasusunan. Gunakan fungsi ini untuk melaksanakan operasi jumlah dengan mudah pada tatasusunan dan mengembalikan hasilnya. Artikel ini akan memperkenalkan cara menggunakan fungsi tatasusunan bahasa Go untuk menjumlahkan dan mengembalikan hasilnya, dengan contoh kod. Mula-mula, mari kita lihat tatasusunan dalam bahasa Go. Tatasusunan ialah struktur data yang menyimpan jujukan elemen bersaiz tetap. Dalam bahasa Go, panjang tatasusunan ditetapkan, dan jenis serta elemen tatasusunan
 Cara menggunakan formula penjumlahan excel - tutorial cara menggunakan formula penjumlahan excel
Mar 05, 2024 pm 12:40 PM
Cara menggunakan formula penjumlahan excel - tutorial cara menggunakan formula penjumlahan excel
Mar 05, 2024 pm 12:40 PM
Ramai rakan masih tidak tahu cara menggunakan formula penjumlahan dalam excel, jadi editor di bawah menerangkan tutorial cara menggunakan formula penjumlahan dalam excel Jika anda memerlukannya, sila lihat saya percaya ia akan membantu semua orang. Langkah 1: Mula-mula kita buka Excel (seperti yang ditunjukkan dalam gambar). Langkah 2: Masukkan antara muka kerja Excel (seperti yang ditunjukkan dalam gambar). Langkah 3: Kemudian kita buka dokumen yang perlu diedit Berikut adalah contoh dokumen (seperti yang ditunjukkan dalam gambar). Langkah 4: Pilih "Jumlah Skor" dan masukkan "=C2+D2+E2" dalam kotak fungsi fx Kemudian tekan kekunci Enter. Jumlah markah telah keluar (seperti yang ditunjukkan dalam gambar). Langkah 5: Klik menu lungsur turun kotak isi. Isikan jumlah markah (seperti yang ditunjukkan dalam rajah). Langkah 6: Isikan drop-down (seperti yang ditunjukkan dalam gambar). Langkah 7:
 Program Java untuk mencetak jumlah nombor
Aug 20, 2023 am 09:49 AM
Program Java untuk mencetak jumlah nombor
Aug 20, 2023 am 09:49 AM
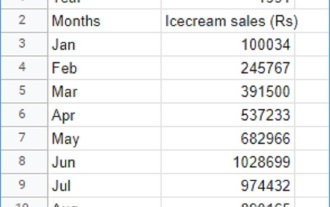
Terdapat cara yang berbeza untuk menambah nombor di Jawa. Nombor yang akan ditambahkan boleh diberikan dalam masa putaran atau boleh dimasukkan terus ke dalam program. Walau bagaimanapun, adalah sukar untuk menambah nombor dalam cara ini jika senarai nombor terlalu besar. Kadangkala, data yang akan ditambahkan diberikan dalam helaian/g



