Program C++ untuk mengira jumlah pepenjuru matriks

Penggunaan tatasusunan atau matriks 2 dimensi amat berfaedah untuk beberapa aplikasi. Baris dan lajur matriks digunakan untuk memegang nombor Kita boleh mentakrifkan 2D Tatasusunan berbilang dimensi digunakan untuk mewakili matriks dalam C++. Dalam artikel ini kita akan melihat bagaimana untuk melaksanakan gunakan C++ untuk mengira hasil tambah pepenjuru bagi matriks segi empat sama.
Matriks mempunyai dua pepenjuru, pepenjuru utama dan pepenjuru sekunder (kadangkala dirujuk sebagai pepenjuru major dan minor). sudut (indeks [0, 0]) ke sudut kanan bawah (indeks [n-1, n-1]) dengan n ialah susunan Matriks segi empat sama. Diagonal utama bermula dari sudut kanan atas (indeks [n-1, 0]) dan berakhir di sudut kiri bawah sudut (indeks [0, n-1] Mari kita lihat algoritma untuk mencari jumlah elemen bersama-sama dengan dua pepenjuru ini.
Terjemahan bahasa Cina bagiJumlah Diagonal Matriks
ialah:Jumlah pepenjuru matriks
$$mulakan{bmatrix} 8&5&3baris baharu 6 & 7& 1baris baharu 2 & 4 & 9 tamat{bmatrix},$$
Sum of all elements in major diagonal: (8 + 7 + 9) = 24 Sum of all elements in minor diagonal: (3 + 7 + 2) = 12
Dalam contoh sebelumnya, satu matriks 3 x 3 telah digunakan secara individu dan dikira jumlahnya Mari kita lihat algoritma dan pelaksanaan untuk jelas pandangan.
Algoritma
- Baca matriks M sebagai input
- Pertimbangkan M dengan n baris dan n lajur
- sum_major := 0
- sum_minor := 0
- Untuk julat i dari 0 hingga n-1, laksanakan
- untuk julat j dari 0 hingga n - 1, lakukan
- jika i dan j adalah sama, maka
- sum_major := sum_major + M[ i ][ j ]
- tamat jika
- jika (i + j) sama dengan (N - 1), maka
- sum_minor := sum_minor + M[ i ][ j ]
- tamat jika
- jika i dan j adalah sama, maka
- tamat untuk
- tamat untuk
- jumlah pulangan
Contoh
#include <iostream>
#include <cmath>
#define N 7
using namespace std;
float solve( int M[ N ][ N ] ){
int sum_major = 0;
int sum_minor = 0;
for ( int i = 0; i < N; i++ ) {
for ( int j = 0; j < N; j++ ) {
if( i == j ) {
sum_major = sum_major + M[ i ][ j ];
}
if( (i + j) == N - 1) {
sum_minor = sum_minor + M[ i ][ j ];
}
}
}
cout << "The sum of major diagonal: " << sum_major << endl;
cout << "The sum of minor diagonal: " << sum_minor << endl;
}
int main(){
int mat1[ N ][ N ] = {
{5, 8, 74, 21, 69, 78, 25},
{48, 2, 98, 6, 63, 52, 3},
{85, 12, 10, 6, 9, 47, 21},
{6, 12, 18, 32, 5, 10, 32},
{8, 45, 74, 69, 1, 14, 56},
{7, 69, 17, 25, 89, 23, 47},
{98, 23, 15, 20, 63, 21, 56},
};
cout << "For the first matrix: " << endl;
solve( mat1 );
int mat2[ N ][ N ] = {
{6, 8, 35, 21, 87, 8, 26},
{99, 2, 36, 326, 25, 24, 56},
{15, 215, 3, 157, 8, 41, 23},
{96, 115, 17, 5, 3, 10, 18},
{56, 4, 78, 5, 10, 22, 58},
{85, 41, 29, 65, 47, 36, 78},
{12, 23, 87, 45, 69, 96, 12}
};
cout << "\nFor the second matrix: " << endl;
solve( mat2 );
}
Output
For the first matrix: The sum of major diagonal: 129 The sum of minor diagonal: 359 For the second matrix: The sum of major diagonal: 74 The sum of minor diagonal: 194
Kesimpulan
Dalam artikel ini, kita telah melihat cara mengira jumlah pepenjuru bagi matriks segi empat sama tertentu. Diagonal utama berjalan dari sudut kiri atas ke sudut kanan bawah, manakala pepenjuru kedua berjalan dari sudut kiri bawah ke sudut kanan atas. Garis pepenjuru bermula dari sudut kanan atas ke sudut kiri bawah. Untuk mencari jumlah ini elemen pepenjuru, kita gelung melalui semua elemen Apabila kedua-dua baris dan nilai indeks lajur Sama, ia mewakili unsur pepenjuru utama apabila jumlah kedua-dua indeks adalah Sama seperti susunan n-1 matriks, ia akan ditambah kepada subpepenjuru prosedur mengambil dua gelung bersarang dan kami melintasi semua elemen yang terdapat dalam Tatasusunan 2D. Oleh itu, mengira jumlah dua pepenjuru akan mengambil masa O(n2) matriks yang diberikan.
Atas ialah kandungan terperinci Program C++ untuk mengira jumlah pepenjuru matriks. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

AI Hentai Generator
Menjana ai hentai secara percuma.

Artikel Panas

Alat panas

Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma

SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan

Hantar Studio 13.0.1
Persekitaran pembangunan bersepadu PHP yang berkuasa

Dreamweaver CS6
Alat pembangunan web visual

SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)

Topik panas
 1377
1377
 52
52
 Bagaimana untuk menjadikan Peta Google sebagai peta lalai dalam iPhone
Apr 17, 2024 pm 07:34 PM
Bagaimana untuk menjadikan Peta Google sebagai peta lalai dalam iPhone
Apr 17, 2024 pm 07:34 PM
Peta lalai pada iPhone ialah Peta, pembekal geolokasi proprietari Apple. Walaupun peta semakin baik, ia tidak berfungsi dengan baik di luar Amerika Syarikat. Ia tiada apa-apa untuk ditawarkan berbanding Peta Google. Dalam artikel ini, kami membincangkan langkah yang boleh dilaksanakan untuk menggunakan Peta Google untuk menjadi peta lalai pada iPhone anda. Cara Menjadikan Peta Google Peta Lalai dalam iPhone Menetapkan Peta Google sebagai aplikasi peta lalai pada telefon anda adalah lebih mudah daripada yang anda fikirkan. Ikut langkah di bawah – Langkah prasyarat – Anda mesti memasang Gmail pada telefon anda. Langkah 1 – Buka AppStore. Langkah 2 – Cari “Gmail”. Langkah 3 – Klik di sebelah apl Gmail
 Pendaraban matriks universal CUDA: dari kemasukan kepada kemahiran!
Mar 25, 2024 pm 12:30 PM
Pendaraban matriks universal CUDA: dari kemasukan kepada kemahiran!
Mar 25, 2024 pm 12:30 PM
Pendaraban Matriks Umum (GEMM) ialah bahagian penting dalam banyak aplikasi dan algoritma, dan juga merupakan salah satu petunjuk penting untuk menilai prestasi perkakasan komputer. Penyelidikan mendalam dan pengoptimuman pelaksanaan GEMM boleh membantu kami lebih memahami pengkomputeran berprestasi tinggi dan hubungan antara perisian dan sistem perkakasan. Dalam sains komputer, pengoptimuman GEMM yang berkesan boleh meningkatkan kelajuan pengkomputeran dan menjimatkan sumber, yang penting untuk meningkatkan prestasi keseluruhan sistem komputer. Pemahaman yang mendalam tentang prinsip kerja dan kaedah pengoptimuman GEMM akan membantu kami menggunakan potensi perkakasan pengkomputeran moden dengan lebih baik dan menyediakan penyelesaian yang lebih cekap untuk pelbagai tugas pengkomputeran yang kompleks. Dengan mengoptimumkan prestasi GEMM
 Cara mengira penambahan, penolakan, pendaraban dan pembahagian dalam dokumen perkataan
Mar 19, 2024 pm 08:13 PM
Cara mengira penambahan, penolakan, pendaraban dan pembahagian dalam dokumen perkataan
Mar 19, 2024 pm 08:13 PM
WORD adalah pemproses perkataan yang berkuasa Kita boleh menggunakan perkataan untuk mengedit pelbagai teks Dalam jadual Excel, kita telah menguasai kaedah pengiraan penambahan, penolakan dan penggandaan Jadi jika kita perlu mengira penambahan nilai dalam jadual Word. Bagaimana untuk menolak pengganda? Bolehkah saya hanya menggunakan kalkulator untuk mengiranya? Jawapannya sudah tentu tidak, WORD juga boleh melakukannya. Hari ini saya akan mengajar anda cara menggunakan formula untuk mengira operasi asas seperti penambahan, penolakan, pendaraban dan pembahagian dalam jadual dalam dokumen Word. Jadi, hari ini izinkan saya menunjukkan secara terperinci cara mengira penambahan, penolakan, pendaraban dan pembahagian dalam dokumen WORD? Langkah 1: Buka WORD, klik [Jadual] di bawah [Sisipkan] pada bar alat dan masukkan jadual dalam menu lungsur.
 Bagaimana untuk menulis program undur mudah dalam C++?
Nov 03, 2023 pm 01:39 PM
Bagaimana untuk menulis program undur mudah dalam C++?
Nov 03, 2023 pm 01:39 PM
C++ ialah bahasa pengaturcaraan yang digunakan secara meluas yang sangat mudah dan praktikal dalam menulis program undur. Program undur ialah aplikasi biasa yang boleh memberikan kita pengiraan masa dan fungsi kira detik yang sangat tepat. Artikel ini akan memperkenalkan cara menggunakan C++ untuk menulis program kira detik yang mudah. Kunci untuk melaksanakan program kira detik ialah menggunakan pemasa untuk mengira peredaran masa. Dalam C++, kita boleh menggunakan fungsi dalam fail pengepala time.h untuk melaksanakan fungsi pemasa. Berikut ialah kod untuk program kira detik yang mudah
 Apl jam tiada dalam iPhone: Cara membetulkannya
May 03, 2024 pm 09:19 PM
Apl jam tiada dalam iPhone: Cara membetulkannya
May 03, 2024 pm 09:19 PM
Adakah apl jam hilang dari telefon anda? Tarikh dan masa masih akan dipaparkan pada bar status iPhone anda. Walau bagaimanapun, tanpa apl Jam, anda tidak akan dapat menggunakan jam dunia, jam randik, jam penggera dan banyak ciri lain. Oleh itu, membetulkan apl jam yang hilang hendaklah berada di bahagian atas senarai tugasan anda. Penyelesaian ini boleh membantu anda menyelesaikan isu ini. Betulkan 1 – Letakkan Apl Jam Jika anda tersilap mengalih keluar apl Jam daripada skrin utama anda, anda boleh meletakkan semula apl Jam pada tempatnya. Langkah 1 – Buka kunci iPhone anda dan mula meleret ke kiri sehingga anda mencapai halaman Pustaka Apl. Langkah 2 – Seterusnya, cari "jam" dalam kotak carian. Langkah 3 – Apabila anda melihat "Jam" di bawah dalam hasil carian, tekan dan tahan dan
 Bagaimana untuk membuka tapak web menggunakan Penjadual Tugas
Oct 02, 2023 pm 11:13 PM
Bagaimana untuk membuka tapak web menggunakan Penjadual Tugas
Oct 02, 2023 pm 11:13 PM
Adakah anda kerap melawat tapak web yang sama pada masa yang hampir sama setiap hari? Ini boleh menyebabkan menghabiskan banyak masa dengan berbilang tab penyemak imbas dibuka dan mengacaukan penyemak imbas semasa melakukan tugas harian. Nah, bagaimana pula dengan membukanya tanpa perlu melancarkan penyemak imbas secara manual? Ia sangat mudah dan tidak memerlukan anda memuat turun sebarang apl pihak ketiga, seperti yang ditunjukkan di bawah. Bagaimanakah cara saya menyediakan Penjadual Tugas untuk membuka tapak web? Tekan kekunci, taip Penjadual Tugas dalam kotak carian, dan kemudian klik Buka. Windows Pada bar sisi kanan, klik pada pilihan Cipta Tugas Asas. Dalam medan Nama, masukkan nama tapak web yang ingin anda buka dan klik Seterusnya. Seterusnya, di bawah Pencetus, klik Kekerapan Masa dan klik Seterusnya. Pilih berapa lama anda mahu acara itu berulang dan klik Seterusnya. Pilih dayakan
 Cara mengira bilangan elemen dalam senarai menggunakan fungsi count() Python
Nov 18, 2023 pm 02:53 PM
Cara mengira bilangan elemen dalam senarai menggunakan fungsi count() Python
Nov 18, 2023 pm 02:53 PM
Cara menggunakan fungsi count() Python untuk mengira bilangan elemen dalam senarai memerlukan contoh kod khusus Sebagai bahasa pengaturcaraan yang berkuasa dan mudah dipelajari, Python menyediakan banyak fungsi terbina dalam untuk mengendalikan struktur data yang berbeza. Salah satunya ialah fungsi count(), yang boleh digunakan untuk mengira bilangan elemen dalam senarai. Dalam artikel ini, kami akan menerangkan cara menggunakan fungsi count() secara terperinci dan memberikan contoh kod khusus. Fungsi count() ialah fungsi terbina dalam Python, digunakan untuk mengira sesuatu
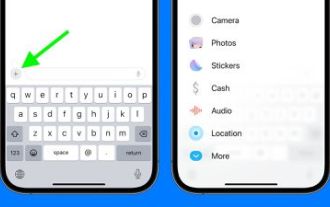 iOS 17: Cara mengatur apl iMessage dalam Messages
Sep 18, 2023 pm 05:25 PM
iOS 17: Cara mengatur apl iMessage dalam Messages
Sep 18, 2023 pm 05:25 PM
Dalam iOS 17, Apple bukan sahaja menambah beberapa ciri pemesejan baharu, tetapi juga mengubah reka bentuk aplikasi Mesej untuk memberikan rupa yang lebih bersih. Semua apl dan alatan iMessage, seperti pilihan kamera dan foto, kini boleh diakses dengan mengetik butang "+" di atas papan kekunci dan di sebelah kiri medan input teks. Mengklik butang "+" memaparkan lajur menu dengan susunan pilihan lalai. Bermula dari bahagian atas, terdapat kamera, foto, pelekat, wang tunai (jika ada), audio dan lokasi. Di bahagian paling bawah terdapat butang "Lagi", yang apabila diketik akan mendedahkan sebarang apl pemesejan lain yang dipasang (anda juga boleh meleret ke atas untuk mendedahkan senarai tersembunyi ini). Cara menyusun semula apl iMessage anda Anda boleh melakukannya dengan mengikuti




