hujung hadapan web
tutorial js
Program JavaScript untuk mengira penyongsangan saiz 3 dalam tatasusunan yang diberikan
Program JavaScript untuk mengira penyongsangan saiz 3 dalam tatasusunan yang diberikan
Dalam tutorial ini, kita akan belajar mengira penyongsangan saiz 3 dalam tatasusunan yang diberikan.
Pernyataan Masalah - Kami diberi susunan panjang n mengandungi entri angka yang berbeza. Kita perlu mencari jumlah bilangan pasangan nombor saiz 3 supaya arr[i] > arr[j] > arr[k], di mana I
Di sini, mula-mula kita akan mempelajari kaedah brute force dan kemudian, kita akan mengoptimumkan kerumitan masa dan ruangnya.
Gunakan kaedah brute force
Dalam pendekatan brute force, kami akan menggunakan tiga gelung bersarang untuk mencari pembalikan kiraan saiz 3. Gelung pertama berulang daripada elemen 1 hingga n-2, dan gelung kedua melelaran daripada elemen ke-i kepada elemen ke-1. Jika elemen sebelumnya lebih besar daripada elemen seterusnya, ulangi tatasusunan dan cari elemen yang lebih kecil daripada elemen tengah.
Tatabahasa
Pengguna boleh menggunakan kaedah brute force seperti di bawah sintaks untuk mengira penyongsangan saiz 3 dalam tatasusunan yang diberikan.
for ( ) {
for ( ) {
if (array[m] > array[n]) {
for (let o = n + 1; o < len; o++) {
if (array[n] > array[o])
cnt++;
}
}
}
}
Algoritma
Langkah 1 - Ulangi elemen n-2 pertama menggunakan gelung for.
Langkah 2 - Lelaran pada elemen m+1 kepada len-1 menggunakan gelung bersarang untuk.
Langkah 3 - Dalam gelung bersarang untuk, semak sama ada tatasusunan[m] lebih besar daripada tatasusunan[n]. Jika ya, lelaran daripada elemen n+1 ke elemen terakhir.
Langkah 4 - Jika elemen pada indeks yang lain adalah kurang daripada elemen pada indeks ke-, kita boleh katakan kita menemui pasangan songsang yang sah bersaiz 3 dan menambah pembolehubah 'cnt' tolak 1.
Langkah 5 - Selepas semua lelaran gelung for selesai, kembalikan nilai "cnt".
Contoh 1
Dalam contoh di bawah, kami melaksanakan kaedah brute force untuk mencari jumlah bilangan pasangan pembalikan saiz 3.
Dalam tatasusunan yang diberikan, pengguna hanya boleh memerhati 2 pasangan penyongsangan dalam output. Pasangan pembalikan pertama ialah (10,5,4) dan pasangan pembalikan kedua ialah (20,5,4).
<html>
<body>
<h3> Using the <i> Brute force approach </i> to Count Inversions of size three in a given array </h3>
<div id = "output"> </div>
<script>
let output = document.getElementById('output');
function InversionCount(array) {
let len = array.length;
let cnt = 0;
for (let m = 0; m < len - 2; m++) {
for (let n = m + 1; n < len - 1; n++) {
if (array[m] > array[n]) {
for (let o = n + 1; o < len; o++) {
if (array[n] > array[o])
cnt++;
}
}
}
}
return cnt;
}
let array = [10, 20, 5, 4, 50, 60, 30, 40];
output.innerHTML += "The count of inversion in the " + array + " is " + InversionCount(array)
</script>
</body>
</html>
Kerumitan masa dan ruang
Kerumitan Masa - Memandangkan kita menggunakan tiga gelung bersarang, kerumitan masa ialah O(n^3).
Kerumitan Angkasa - Apabila kita menggunakan ruang malar, kerumitan ruang ialah O(1).
Gunakan dua bersarang untuk gelung
Dalam kaedah ini kita akan menggunakan dua gelung bersarang. Kami akan mencari jumlah bilangan elemen yang lebih kecil di sebelah kanan elemen semasa, dan jumlah bilangan elemen yang lebih besar di sebelah kiri. Selepas itu, kita darabkan kedua-duanya untuk mendapatkan jumlah bilangan penyongsangan untuk nombor tertentu.
Tatabahasa
Pengguna boleh mengikuti sintaks di bawah untuk mengira pembalikan saiz 3 dalam JavaScript menggunakan dua gelung bersarang.
for ( ) {
// find a smaller element on the right
for ()
if (array[m] < array[n])
right++;
// find bigger elements on the left
for ()
if (array[m] > array[n])
left++;
cnt += right * left;
}
Algoritma
Langkah 1 - Lelaran ke atas n elemen tatasusunan menggunakan gelung for.
Langkah 2 - Gunakan gelung for untuk mencari semua elemen di sebelah kanan elemen semasa yang lebih kecil daripada elemen semasa.
Langkah 3 - Gunakan gelung for sekali lagi untuk mencari semua elemen di sebelah kiri elemen semasa yang lebih besar daripada elemen semasa.
Langkah 4 - Darabkan nilai pembolehubah kiri dan kanan dan tambahkannya pada pembolehubah "cnt".
Contoh 2
Dalam contoh di bawah, kami menggunakan dua gelung bersarang untuk mencari jumlah bilangan pembalikan saiz 3 seperti yang ditunjukkan dalam kaedah di atas. Pengguna boleh melihat bahawa output adalah sama seperti dalam kaedah pertama.
<html>
<body>
<h3> Using the <i> two nested loops </i> to Count Inversions of size three in a given array </h3>
<div id = "output"> </div>
<script>
let output = document.getElementById('output');
function InversionCount(array) {
let cnt = 0;
let len = array.length;
// Iterate through every element of the array
for (let m = 0; m < len - 1; m++) {
// count all element that are smaller than arr[m] and at the right to it
let right = 0;
for (let n = m - 1; n >= 0; n--)
if (array[m] < array[n])
right++;
// count all element that are greater than arr[m] and at the left to it
let left = 0;
for (let n = m + 1; n < len; n++)
if (array[m] > array[n])
left++;
// multiply left greater and right smaller elements
cnt += right * left;
}
return cnt;
}
let array = [10, 20, 5, 4, 50, 60, 30, 40];
output.innerHTML += "The count of inversion in the " + array + " is " + InversionCount(array)
</script>
</body>
</html>
Kerumitan masa dan ruang
Kerumitan Masa - Memandangkan kita menggunakan dua gelung bersarang, kerumitan masa kaedah di atas ialah O(n^2).
Kerumitan Angkasa - Apabila kita menggunakan ruang malar, kerumitan ruang ialah O(1).
Pengguna mempelajari dua kaedah untuk mencari pembalikan kiraan saiz 3 dalam tatasusunan yang diberikan. Dalam pendekatan pertama, kami menyelesaikan masalah menggunakan pendekatan kekerasan, dan dalam pendekatan kedua, kami terus mengoptimumkan penyelesaian untuk mengurangkan kerumitan masa.
Atas ialah kandungan terperinci Program JavaScript untuk mengira penyongsangan saiz 3 dalam tatasusunan yang diberikan. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
Alat AI Hot
Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik
AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.
Undress AI Tool
Gambar buka pakaian secara percuma
Clothoff.io
Penyingkiran pakaian AI
AI Hentai Generator
Menjana ai hentai secara percuma.
Artikel Panas
Alat panas
Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma
SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan
Hantar Studio 13.0.1
Persekitaran pembangunan bersepadu PHP yang berkuasa
Dreamweaver CS6
Alat pembangunan web visual
SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)
Topik panas
Ganti aksara rentetan dalam javascript
Mar 11, 2025 am 12:07 AM
Penjelasan terperinci mengenai kaedah penggantian rentetan javascript dan Soalan Lazim Artikel ini akan meneroka dua cara untuk menggantikan watak rentetan dalam JavaScript: Kod JavaScript dalaman dan HTML dalaman untuk laman web. Ganti rentetan di dalam kod JavaScript Cara yang paling langsung ialah menggunakan kaedah pengganti (): str = str.replace ("cari", "ganti"); Kaedah ini hanya menggantikan perlawanan pertama. Untuk menggantikan semua perlawanan, gunakan ungkapan biasa dan tambahkan bendera global g: str = str.replace (/fi
Tutorial Persediaan API Carian Google Custom
Mar 04, 2025 am 01:06 AM
Tutorial ini menunjukkan kepada anda bagaimana untuk mengintegrasikan API carian Google tersuai ke dalam blog atau laman web anda, menawarkan pengalaman carian yang lebih halus daripada fungsi carian tema WordPress standard. Ia menghairankan mudah! Anda akan dapat menyekat carian ke y
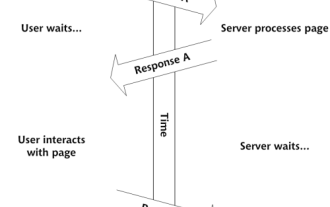
Bina Aplikasi Web Ajax anda sendiri
Mar 09, 2025 am 12:11 AM
Jadi di sini anda, bersedia untuk mempelajari semua perkara ini yang dipanggil Ajax. Tetapi, apa sebenarnya? Istilah Ajax merujuk kepada kumpulan teknologi longgar yang digunakan untuk membuat kandungan web yang dinamik dan interaktif. Istilah Ajax, yang asalnya dicipta oleh Jesse J
Contoh warna json fail
Mar 03, 2025 am 12:35 AM
Siri artikel ini ditulis semula pada pertengahan 2017 dengan maklumat terkini dan contoh segar. Dalam contoh JSON ini, kita akan melihat bagaimana kita dapat menyimpan nilai mudah dalam fail menggunakan format JSON. Menggunakan notasi pasangan nilai utama, kami boleh menyimpan apa-apa jenis
10 JQuery Syntax Highlighters
Mar 02, 2025 am 12:32 AM
Tingkatkan Penyampaian Kod Anda: 10 Penyeret Sintaks untuk Pemaju Coretan kod perkongsian di laman web atau blog anda adalah amalan biasa bagi pemaju. Memilih penyapu sintaks yang betul dapat meningkatkan daya tarikan dan daya tarikan visual dengan ketara. T
8 plugin susun atur halaman jquery yang menakjubkan
Mar 06, 2025 am 12:48 AM
Leverage JQuery untuk Layouts Laman Web yang mudah: 8 Plugin Essential JQuery memudahkan susun atur laman web dengan ketara. Artikel ini menyoroti lapan plugin jQuery yang kuat yang menyelaraskan proses, terutamanya berguna untuk penciptaan laman web manual
10 JavaScript & JQuery MVC Tutorial
Mar 02, 2025 am 01:16 AM
Artikel ini membentangkan pemilihan lebih daripada 10 tutorial mengenai rangka kerja javascript dan jquery model-view-controller (MVC), sesuai untuk meningkatkan kemahiran pembangunan web anda pada tahun baru. Tutorial ini merangkumi pelbagai topik, dari Foundatio
Apa itu ' ini ' Dalam JavaScript?
Mar 04, 2025 am 01:15 AM
Mata teras Ini dalam JavaScript biasanya merujuk kepada objek yang "memiliki" kaedah, tetapi ia bergantung kepada bagaimana fungsi dipanggil. Apabila tidak ada objek semasa, ini merujuk kepada objek global. Dalam penyemak imbas web, ia diwakili oleh tetingkap. Apabila memanggil fungsi, ini mengekalkan objek global; tetapi apabila memanggil pembina objek atau mana -mana kaedahnya, ini merujuk kepada contoh objek. Anda boleh mengubah konteks ini menggunakan kaedah seperti panggilan (), memohon (), dan mengikat (). Kaedah ini memanggil fungsi menggunakan nilai dan parameter yang diberikan. JavaScript adalah bahasa pengaturcaraan yang sangat baik. Beberapa tahun yang lalu, ayat ini
