Program C++ untuk mencari vektor dan jejak biasa

Tatasusunan atau matriks dua dimensi sangat berguna dalam beberapa aplikasi. Matriks mempunyai baris dan lajur dan menyimpan nombor di dalamnya. Dalam C++, kita juga boleh menggunakan tatasusunan berbilang dimensi untuk menentukan matriks dua dimensi. Dalam artikel ini, kita akan melihat cara mengira norma dan surih matriks tertentu menggunakan C++.
Normal ialah punca kuasa dua hasil tambah semua unsur dalam matriks. Surih ialah jumlah unsur yang terdapat dalam pepenjuru utama. Mari kita lihat algoritma dan perwakilan kod C++.
Matriks biasa
$begin{bmatrix} 5 & 1 & 8 aksara baris baharu 4 & 3 & 9 aksara baris baharu 2&7&3 tamat{bmatrix},$
Sum of all elements: (5 + 1 + 8 + 4 + 3 + 9 + 2 + 7 + 3) = 42 Normal: (Square root of the sum of all elements) = √42 = 6.48
Dalam contoh di atas, kami mengambil matriks 3 x 3, di sini kami mendapat jumlah semua elemen dan kemudian mengambil punca kuasa duanya. Mari kita lihat algoritma untuk pemahaman yang lebih baik.
Algoritma
- Baca matriks M sebagai input
- Pertimbangkan M dengan n baris dan n lajur
- Jumlah: = 0
- Untuk saya dari 1 hingga n, lakukan
- Untuk j dari 1 hingga n, lakukan perkara berikut
- jumlah := jumlah + M[ i ][ j ]
- Tamatkan gelung
- Untuk j dari 1 hingga n, lakukan perkara berikut
- Tamatkan gelung
- res := jumlah punca kuasa dua
- Kembalikan hasil
Contoh
#include <iostream>
#include <cmath>
#define N 5
using namespace std;
float solve( int M[ N ][ N ] ){
int sum = 0;
for ( int i = 0; i < N; i++ ) {
for ( int j = 0; j < N; j++ ) {
sum = sum + M[ i ][ j ];
}
}
return sqrt( sum );
}
int main(){
int mat1[ N ][ N ] = {
{5, 8, 74, 21, 69},
{48, 2, 98, 6, 63},
{85, 12, 10, 6, 9},
{6, 12, 18, 32, 5},
{8, 45, 74, 69, 1},
};
cout << "Normal of the first matrix is: " << solve( mat1 ) << endl;
int mat2[ N ][ N ] = {
{6, 8, 35, 21, 87},
{99, 2, 36, 326, 25},
{15, 215, 3, 157, 8},
{96, 115, 17, 5, 3},
{56, 4, 78, 5, 10},
};
cout << "Normal of the second matrix is: " << solve( mat2 ) << endl;
}
Output
Normal of the first matrix is: 28.0357 Normal of the second matrix is: 37.8418
Jejak Matriks
$begin{bmatrix} 5 & 1 & 8 aksara baris baharu 4 & 3 & 9 aksara baris baharu 2&7&3 tamat{bmatrix},$
Sum of all elements in main diagonal: (5 + 3 + 3) = 11 which is the trace of given matrix
Dalam contoh di atas, kami mengambil matriks 3 x 3 dan di sini kami mendapat jumlah semua elemen pada pepenjuru utama. Jumlah ini ialah surih matriks. Mari kita lihat algoritma untuk pemahaman yang lebih baik.
Algoritma
- Baca matriks M sebagai input
- Pertimbangkan M dengan n baris dan n lajur
- Jumlah: = 0
- Untuk saya dari 1 hingga n, lakukan
- jumlah := jumlah + M[ i ][ i ]
- Tamatkan gelung
- Kembalikan jumlah
Contoh
#include <iostream>
#include <cmath>
#define N 5
using namespace std;
float solve( int M[ N ][ N ] ){
int sum = 0;
for ( int i = 0; i < N; i++ ) {
sum = sum + M[ i ][ i ];
}
return sum;
}
int main(){
int mat1[ N ][ N ] = {
{5, 8, 74, 21, 69},
{48, 2, 98, 6, 63},
{85, 12, 10, 6, 9},
{6, 12, 18, 32, 5},
{8, 45, 74, 69, 1},
};
cout << "Trace of the first matrix is: " << solve( mat1 ) << endl;
int mat2[ N ][ N ] = {
{6, 8, 35, 21, 87},
{99, 2, 36, 326, 25},
{15, 215, 3, 157, 8},
{96, 115, 17, 5, 3},
{56, 4, 78, 5, 10},
};
cout << "Trace of the second matrix is: " << solve( mat2 ) << endl;
}
Output
Trace of the first matrix is: 50 Trace of the second matrix is: 26
Kesimpulan
Normal dan jejak adalah kedua-dua operasi matriks. Untuk melaksanakan kedua-dua operasi ini, kita memerlukan matriks segi empat sama (kerana matriks surih persegi diperlukan). Normal hanyalah punca kuasa dua hasil tambah semua unsur yang terdapat dalam matriks, dan surih ialah jumlah unsur yang terdapat pada pepenjuru utama matriks. Matriks ini boleh diwakili menggunakan tatasusunan dua dimensi dalam C++. Di sini kami memberikan dua contoh matriks dengan 5 baris dan 5 lajur (25 elemen secara keseluruhan). Mengakses matriks memerlukan pernyataan gelung dengan operasi pengindeksan. Untuk pengiraan biasa kita perlu mengulangi setiap elemen, jadi dua gelung bersarang diperlukan. Kerumitan program ini ialah O(n2). Untuk pengesanan, kerana kita hanya perlu melihat pepenjuru utama, indeks baris dan indeks lajur akan sama. Jadi hanya satu untuk gelung sudah memadai. Boleh dikira dalam masa O(n).
Atas ialah kandungan terperinci Program C++ untuk mencari vektor dan jejak biasa. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

AI Hentai Generator
Menjana ai hentai secara percuma.

Artikel Panas

Alat panas

Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma

SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan

Hantar Studio 13.0.1
Persekitaran pembangunan bersepadu PHP yang berkuasa

Dreamweaver CS6
Alat pembangunan web visual

SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)

Topik panas
 1378
1378
 52
52
 Terjemahkan yang berikut ke dalam bahasa Cina: Program C untuk menukar angka Rom kepada nombor perpuluhan
Sep 05, 2023 pm 09:53 PM
Terjemahkan yang berikut ke dalam bahasa Cina: Program C untuk menukar angka Rom kepada nombor perpuluhan
Sep 05, 2023 pm 09:53 PM
Diberikan di bawah adalah algoritma bahasa C untuk menukar angka Rom kepada nombor perpuluhan: Algoritma Langkah 1 - Mulakan Langkah 2 - Baca angka Rom pada masa jalan Langkah 3 - Panjang: = strlen(roman) Langkah 4 - Untuk i=0 kepada Length-1 Langkah 4.1-suis(roman[i]) Langkah 4.1.1-case'm': &nbs
 Program C++ untuk membandingkan susunan leksikografi dua rentetan
Sep 04, 2023 pm 05:13 PM
Program C++ untuk membandingkan susunan leksikografi dua rentetan
Sep 04, 2023 pm 05:13 PM
Perbandingan rentetan leksikografi bermaksud rentetan dibandingkan dalam susunan kamus. Contohnya, jika terdapat dua rentetan 'epal' dan 'rayuan', rentetan pertama akan datang yang terakhir kerana tiga aksara pertama 'aplikasi' adalah sama. Kemudian untuk rentetan pertama aksara ialah 'l' dan dalam rentetan kedua aksara keempat ialah 'e'. Memandangkan 'e' lebih pendek daripada 'l', ia akan didahulukan jika kita menyusun mengikut leksikografi. Rentetan dibandingkan secara leksikografi sebelum disusun. Dalam artikel ini, kita akan melihat teknik yang berbeza untuk membandingkan dua rentetan secara leksikografi menggunakan C++. Menggunakan fungsi compare() dalam rentetan C++ Objek rentetan C++ mempunyai compare()
 Program C++ untuk mencari nilai fungsi sinus hiperbolik songsang mengambil nilai yang diberikan sebagai hujah
Sep 17, 2023 am 10:49 AM
Program C++ untuk mencari nilai fungsi sinus hiperbolik songsang mengambil nilai yang diberikan sebagai hujah
Sep 17, 2023 am 10:49 AM
Fungsi hiperbola ditakrifkan menggunakan hiperbola dan bukannya bulatan dan bersamaan dengan fungsi trigonometri biasa. Ia mengembalikan parameter nisbah dalam fungsi sinus hiperbolik dari sudut yang dibekalkan dalam radian. Tetapi lakukan sebaliknya, atau dengan kata lain. Jika kita ingin mengira sudut daripada sinus hiperbolik, kita memerlukan operasi trigonometri hiperbolik songsang seperti operasi sinus songsang hiperbolik. Kursus ini akan menunjukkan cara menggunakan fungsi sinus songsang hiperbolik (asinh) dalam C++ untuk mengira sudut menggunakan nilai sinus hiperbolik dalam radian. Operasi arcsine hiperbolik mengikut formula berikut -$$\mathrm{sinh^{-1}x\:=\:In(x\:+\:\sqrt{x^2\:+\:1})}, Di mana\:In\:is\:logaritma asli\:(log_e\:k)
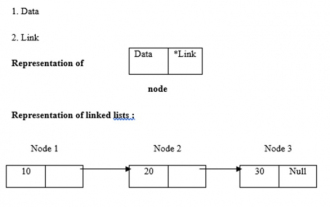 Program C untuk mencari panjang senarai terpaut
Sep 07, 2023 pm 07:33 PM
Program C untuk mencari panjang senarai terpaut
Sep 07, 2023 pm 07:33 PM
Senarai terpaut menggunakan peruntukan memori dinamik, iaitu ia berkembang dan mengecut dengan sewajarnya. Ia ditakrifkan sebagai koleksi nod. Di sini, nod mempunyai dua bahagian, data dan pautan. Data, pautan dan senarai terpaut diwakili seperti berikut - Jenis senarai terpaut Terdapat empat jenis senarai terpaut, seperti berikut: - Senarai pautan tunggal / Senarai pautan tunggal Senarai berganda / Berganda Pekeliling Senarai pautan tunggal Pekeliling Senarai pautan berganda Kami menggunakan kaedah rekursif untuk mencari panjang senarai terpaut Logiknya ialah -intlength(nod *temp){ if(temp==NULL) returnl{&n
 Program C menggunakan fungsi rename() untuk menukar nama fail
Sep 21, 2023 pm 10:01 PM
Program C menggunakan fungsi rename() untuk menukar nama fail
Sep 21, 2023 pm 10:01 PM
Fungsi nama semula menukar fail atau direktori daripada nama lamanya kepada nama baharunya. Operasi ini serupa dengan operasi bergerak. Jadi kita juga boleh menggunakan fungsi nama semula ini untuk memindahkan fail. Fungsi ini wujud dalam fail pengepala perpustakaan stdio.h. Sintaks fungsi nama semula adalah seperti berikut: intrename(constchar*oldname,constchar*newname); Fungsi rename() fungsi menerima dua parameter. Satu nama lama dan satu lagi nama baru. Kedua-dua parameter adalah penunjuk kepada aksara malar yang mentakrifkan nama lama dan baharu fail. Mengembalikan sifar jika fail berjaya dinamakan semula, jika tidak, mengembalikan integer bukan sifar. Semasa operasi menamakan semula
 Program C++ untuk mencetak kamus
Sep 11, 2023 am 10:33 AM
Program C++ untuk mencetak kamus
Sep 11, 2023 am 10:33 AM
Peta ialah sejenis bekas khas dalam C++ di mana setiap elemen adalah sepasang dua nilai, iaitu nilai kunci dan nilai dipetakan. Nilai kunci digunakan untuk mengindeks setiap item, dan nilai yang dipetakan ialah nilai yang dikaitkan dengan kunci. Tidak kira sama ada nilai yang dipetakan adalah unik, kuncinya sentiasa unik. Untuk mencetak elemen peta dalam C++ kita perlu menggunakan iterator. Elemen dalam set item ditunjukkan oleh objek iterator. Iterator digunakan terutamanya dengan tatasusunan dan jenis bekas lain (seperti vektor), dan mereka mempunyai set operasi khusus yang boleh digunakan untuk mengenal pasti elemen tertentu dalam julat tertentu. Iterator boleh dinaikkan atau dikurangkan untuk merujuk elemen berbeza yang terdapat dalam julat atau bekas. Peulang menunjuk ke lokasi memori elemen tertentu dalam julat. Mencetak peta dalam C++ menggunakan iterator Mula-mula, mari lihat cara untuk mentakrifkan
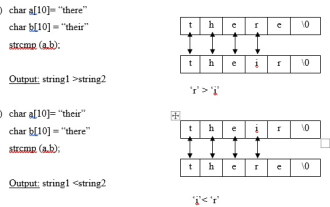 Tulis program C yang menggunakan fungsi perpustakaan strncmp untuk membandingkan dua rentetan
Sep 09, 2023 pm 01:17 PM
Tulis program C yang menggunakan fungsi perpustakaan strncmp untuk membandingkan dua rentetan
Sep 09, 2023 pm 01:17 PM
Strncmp ialah fungsi perpustakaan yang dipratentukan, terdapat dalam fail string.h, yang digunakan untuk membandingkan dua rentetan dan memaparkan rentetan yang lebih besar. fungsi strcmp (perbandingan rentetan) Fungsi ini membandingkan dua rentetan. Ia mengembalikan perbezaan ASCII bagi aksara tidak sepadan pertama dalam dua rentetan. Sintaks instrcmp(string1,string2); Jika perbezaannya sama dengan sifar, maka string1=string2. Jika perbezaan adalah positif, string1>string2. Jika perbezaannya negatif, string1<string2. Contoh fungsi strncmp Fungsi ini digunakan untuk membandingkan n aksara pertama dua rentetan. sintaks strn
 Program C++ untuk mendapatkan bahagian khayalan nombor kompleks yang diberikan
Sep 06, 2023 pm 06:05 PM
Program C++ untuk mendapatkan bahagian khayalan nombor kompleks yang diberikan
Sep 06, 2023 pm 06:05 PM
Sains moden sangat bergantung pada konsep nombor jamak, yang pertama kali ditubuhkan pada awal abad ke-17 oleh Girolamo Cardano, yang memperkenalkannya pada abad ke-16. Formula untuk nombor kompleks ialah a+ib, dengan a memegang kod html dan b ialah nombor nyata. Nombor kompleks dikatakan mempunyai dua bahagian: bahagian nyata <a> dan bahagian khayalan (<ib>). Nilai i atau iota ialah √-1. Kelas jamak dalam C++ ialah kelas yang digunakan untuk mewakili nombor kompleks. Kelas kompleks dalam C++ boleh mewakili dan mengawal beberapa operasi nombor kompleks. Mari kita lihat bagaimana untuk mewakili dan mengawal paparan nombor majmuk. imag() fungsi ahli Seperti yang dinyatakan di atas, nombor kompleks terdiri daripada bahagian nyata dan bahagian khayalan. Untuk memaparkan bahagian sebenar kami menggunakan real()




