Kira jarak maksimum antara dua titik pada satah koordinat menggunakan kaedah angkup berputar

Dalam C++ kami mempunyai fungsi sqrt yang dipratentukan yang mengembalikan punca kuasa dua sebarang nombor. Kaedah angkup berputar ialah teknik yang digunakan dalam penyelesaian algoritma atau geometri pengiraan.

Perwakilan Visual Kaedah Angkup Berputar

Putaran Tangan menunjukkan contoh sebenar plot angkup berputar, menunjukkan orientasi menegak setiap kali tangan diputar. Kita juga boleh memahami konsep ini dengan menggunakan poligon.

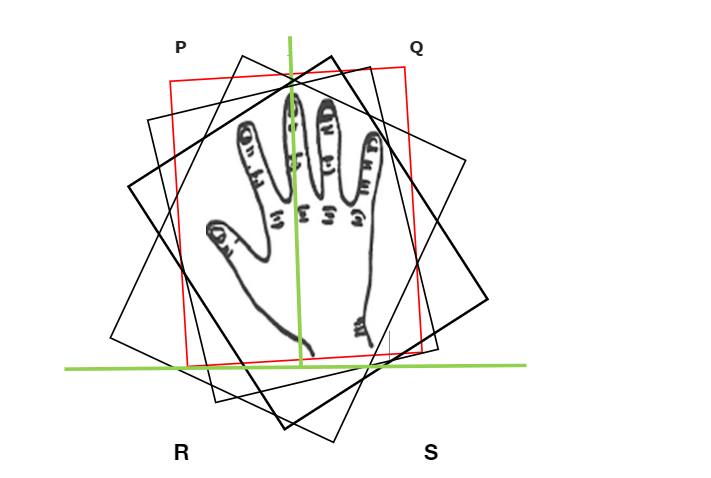
Dalam artikel ini, kita akan menggunakan kaedah angkup berputar untuk mencari jarak maksimum antara dua titik koordinat. 跨度>

Tatabahasa

Sintaks berikut digunakan dalam program -

vector<datatype> name

Parameter

• Vektor - Kami bermula dengan vektor kata kunci dan memulakan vektor dalam C++.

• datatype - Jenis elemen data yang diwakili oleh vektor.

• nama - Nama vektor.

Algoritma

• Kami akan menggunakan fail pengepala iostream, vector dan cmath untuk memulakan program.

• Kami sedang mencipta titik nama struktur yang akan menyimpan koordinat x dan y.

• Kami sedang mentakrifkan takrifan fungsi jenis data berganda jarak() untuk mengira jarak antara dua titik koordinat. Di sini, Titik p1 dan Titik p2 ialah parameter yang menerima nilai koordinat dan jarak pulangan menggunakan formula sqrt dan jarak fungsi yang telah ditetapkan.

• Kami mentakrifkan definisi fungsi yang dipanggil CP() yang jenis data bergandanya menerima parameter Titik p1, Titik p2 dan Titik p3 untuk mengira vektor hasil silang, iaitu p2-p1 dan -p3 w.r.t koordinat x dan y.

• Sekarang kami sedang mencipta definisi fungsi jenis data berganda

  rotatingCaliper() yang mengambil hujah sebagai vektor titik dan memaksimumkan jarak antara mana-mana dua satah koordinat.

• Kami memulakan hasil pembolehubah kepada

  0 yang akan dijejaki untuk memenuhi pengiraan jarak maksimum. Untuk mencari saiz titik, ia akan menggunakan fungsi yang dipratentukan dipanggil size() dan menyimpannya dalam pembolehubah n.

• Kami memulakan dua pembolehubah

  j dan k kepada 1 dan melakukan perkara berikut -

• Kami bergerak

  j ke titik seterusnya dalam poligon dan hasil silang CP i+1] % n' tepi semasa 'titik[i], mata[ dan tepi seterusnya 'mata [ j]' adalah kurang daripada CP hasil silang bagi tepi semasa 'titik[i]', mata[ (i + 1) % n]' dan titik seterusnya ' selepas titik [(j + 1) % n]' tepi. Ini akan mengesahkan bahawa tepi semasa adalah berserenjang dengan tepi seterusnya.

• Kami bergerak

  k ke titik seterusnya dalam poligon sehingga jarak antara titik semasa 'titik[i]' dan titik seterusnya ' titik[k]' lebih kecil daripada titik semasa 'titik [ Jarak ' antara i]' dan titik selepas titik seterusnya 'mata[(k+1)%n]. Ini akan mengesahkan bahawa titik seterusnya adalah paling jauh dari titik semasa.

• Sekarang kita sedang mengira jarak antara titik

  j, k, dan titik semasa 'titik[i]', mendarab semua titik ini dan kemudian kita akan mendapat nilai maksimum dalam pembolehubah hasil.

• Kami memulakan fungsi utama dan menggunakan nilai satah koordinat pada pembolehubah

  "vektor titik".

• Akhir sekali, kami memanggil nama fungsi

  rotatingCaliper() dan lulus nilai 'points' sebagai parameter untuk mendapatkan jarak maksimum plot caliper berputar.

Contoh

Dalam program ini kita akan menggunakan kaedah angkup berputar untuk melakukan jarak maksimum antara dua titik dalam satah koordinat.

#include <iostream>
#include <vector>
#include <cmath>
using namespace std;
struct Point {
    double x, y;
};
// In this function we are calculating the distance between two coordinate point.
double distance(Point p1, Point p2) {
   return sqrt((p2.x - p1.x) * (p2.x - p1.x) + (p2.y - p1.y) * (p2.y - p1.y));
}
// In this function we are calculating the cross-product of two vector
double CP(Point p1, Point p2, Point p3) // CP: cross-product {
   return (p2.x - p1.x) * (p3.y - p1.y) - (p2.y - p1.y) * (p3.x - p1.x);
}
// In this function we are calculating the Rotating Caliper
double rotatingCalipers(vector<Point> points) {
   double result = 0;
  int n = points.size();
    int j = 1, k = 1;
   for (int i = 0; i < n; i++) {
       while (CP(points[i], points[(i + 1) % n], points[j]) < CP(points[i], points[(i + 1) % n], points[(j + 1) % n])) 
       {
           j = (j + 1) % n;
       }
       while (distance(points[i], points[k]) < distance(points[i], points[(k + 1) % n])) {
          k = (k + 1) % n;
       }
     // calculate the max distance
        result = max(result, distance(points[i], points[j]) * distance(points[i], points[k]));
   }
   return result;
}
int main() {
    vector<Point> points = {{0, 0}, {1, 1}, {1, 2}, {2, 2}, {2, 3}, {3, 3}, {3, 4}, {4, 4}, {4, 5}, {5, 5},{5,6}};
    cout << "Maximum distance between two coordinate points: "<<rotatingCalipers(points) << endl;
    return 0;
}

Output

Maximum distance between two coordinate points: 39.0512

Kesimpulan

Kami memahami konsep kaedah angkup berputar dengan mengira jarak maksimum antara dua titik koordinat. Aplikasi praktikal kaedah ini termasuk pengoptimuman sudut apertur, klasifikasi pembelajaran mesin, dsb.

Atas ialah kandungan terperinci Kira jarak maksimum antara dua titik pada satah koordinat menggunakan kaedah angkup berputar. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!