 pembangunan bahagian belakang
pembangunan bahagian belakang
 C++
C++
 Kos minimum untuk menukar 1 kepada N, yang boleh dicapai dengan mendarab dengan X atau putaran kanan nombor
Kos minimum untuk menukar 1 kepada N, yang boleh dicapai dengan mendarab dengan X atau putaran kanan nombor
Kos minimum untuk menukar 1 kepada N, yang boleh dicapai dengan mendarab dengan X atau putaran kanan nombor

Kita boleh menggunakan teknik berikut untuk mencari cara termurah untuk mendarab X atau memutarkan nombornya dari 1 ke N. Untuk memantau kos minimum awal, buat pembolehubah kos. Apabila pergi dari N ke 1, semak sama ada N boleh dibahagi dengan X pada setiap peringkat. Jika ya, kemas kini dengan membahagikan N dengan X dan teruskan proses. Jika N tidak boleh dibahagikan dengan X, maka gelungkan digit N ke kanan untuk meningkatkan nilainya. Tambahkan pembolehubah kos dalam kes ini. Nilai pembolehubah kos akhir ialah jumlah minimum yang diperlukan untuk menukar 1 kepada N. Algoritma dengan cekap menentukan operasi minimum yang diperlukan untuk melakukan transformasi yang diingini menggunakan putaran atau pendaraban berangka.
Kaedah penggunaan
Pendekatan Naif: Putaran nombor yang betul
Kaedah yang cekap: darab dengan X
Cara mudah: nombor putar ke kanan
Pendekatan naif adalah bermula dengan nombor 1 dan berulang kali putarkan nombornya ke kanan sehingga anda mencapai nombor sasaran N. Pada setiap putaran, nombor terakhir bertukar kepada nombor pertama. Walaupun secara konsepnya mudah, strategi ini boleh menjadi tidak cekap untuk nilai N yang besar dan mungkin memerlukan banyak langkah untuk mencapai nombor sasaran. Apabila N meningkat, bilangan putaran juga meningkat dengan cepat, menjadikannya kaedah yang kurang berkesan untuk menentukan kos minimum untuk menukar 1 kepada N. Oleh kerana ketidakcekapannya, kaedah ini tidak disyorkan untuk nilai N yang besar, manakala kaedah lain, seperti membahagikan N dengan X, telah terbukti lebih cekap dalam mencari kos transformasi yang paling rendah.
Algoritma
Buat "kos" pembolehubah untuk menjejaki langkah yang diperlukan untuk mencapai N dan mulakannya kepada 1 untuk mewakili nilai semasa.
-
Ulang arahan ini sehingga nombor semasa sama dengan N:
Putar digit nombor semasa ke kanan supaya digit terakhir menjadi digit pertama.
Rekodkan bilangan putaran yang diperlukan dengan menambah pembolehubah "kos" sebanyak 1.
Setelah nombor semasa bersamaan dengan N, pembolehubah "kos" akan menyimpan bilangan langkah minimum yang diperlukan untuk memutarkan integer asal (1) kepada N menggunakan putaran kanan.
Contoh
#include <iostream>
#include <cmath>
int rotateDigits(int num, int numDigits) {
return (num / 10) + (num % 10) * std::pow(10, numDigits - 1);
}
int main() {
int N = 123; // Replace this with your desired N value
int current = 1;
int cost = 0;
bool found = false;
while (current != N) {
int numDigits = std::to_string(current).length();
current = rotateDigits(current, numDigits);
cost++;
if (cost > N) {
std::cout << "N cannot be reached from 1 using right rotations." << std::endl;
found = true;
break;
}
}
if (!found) {
std::cout << "Minimum steps to reach N: " << cost << std::endl;
}
return 0;
}
Output
N cannot be reached from 1 using right rotations.
Kaedah yang cekap: darab dengan X
Cara terbaik untuk meminimumkan kos pendaraban 1 dengan N adalah dengan membahagikan N dengan X secara berkala sehingga hasilnya ialah 1. Untuk mencapai matlamat ini, mulakan pembolehubah kos untuk memantau kos minimum. Kami menentukan sama ada N boleh dibahagikan dengan X dengan bermula dengan nilai N. Jika kedua-dua N dan X boleh dibahagikan, kos meningkat dan operasi pembahagian dilakukan. Ulangi proses ini sehingga N sama dengan 1. Kaedah ini lebih cekap daripada "putaran nombor kanan" kerana ia memerlukan lebih sedikit langkah untuk mendapatkan hasil 1. Oleh kerana sifatnya yang lebih cepat dan lebih cekap, ia adalah kaedah pilihan untuk menentukan kos pensuisan terendah.
Algoritma
Untuk menjejaki kos minimum, mulakan "kos" pembolehubah kepada 0.
Mulakan dari nombor sasaran yang diberikan N, menggunakan pengganda tetap X.
Selagi N lebih besar daripada 1, ulangi langkah 4 hingga 6.
Dengan mengandaikan N% X == 0, tentukan sama ada N boleh dibahagi dengan X.
Jika N boleh dibahagi (N = N / X), bahagikan N dengan X dan tambah 1 pada pembolehubah "kos".
Jika tidak boleh dibahagikan, gelungkan nombor N ke kanan (dengan menggerakkan digit terakhir ke angka pertama) dan naikkan "kos" sebanyak 1.
Ulang langkah 3 hingga 6 sehingga N menjadi 1.
"Kos" terakhir mewakili minimum yang diperlukan untuk mendarab dengan X atau mengalihkan nombor ke kanan untuk menukar 1 kepada N.
Contoh
#include <iostream>
#include <cmath>
int main() {
int X = 3;
int N = 100;
int cost = 0;
while (N > 1) {
if (N % X == 0) {
N /= X;
cost++;
} else {
int lastDigit = N % 10;
N = (N / 10) + (lastDigit * std::pow(10, std::floor(std::log10(N))));
cost++;
}
}
std::cout << "Final cost: " << cost << std::endl;
return 0;
}
Output
Final cost: 2
Kesimpulan
Ringkasnya, apabila ia datang untuk menentukan kos terendah untuk menukar 1 kepada N dengan mendarab dengan X atau memusingkan nombor ke kanan, kaedah yang cekap untuk mendarab dengan Pendekatan yang lebih diperkemas yang disediakan oleh kaedah yang cekap memerlukan lebih sedikit langkah untuk mencapai bilangan N yang diperlukan. Sebaliknya, kaedah naif boleh menjadi tidak berkesan dan memakan masa, terutamanya untuk nilai N yang lebih tinggi. Kita boleh mengurangkan proses yang diperlukan dan menggunakan kaedah yang cekap untuk menentukan cara paling menjimatkan untuk menukar 1 kepada N. Strategi ini menyelesaikan masalah menentukan kos minimum proses penukaran ini dan terbukti sebagai algoritma yang lebih berguna dan cekap.
Atas ialah kandungan terperinci Kos minimum untuk menukar 1 kepada N, yang boleh dicapai dengan mendarab dengan X atau putaran kanan nombor. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

AI Hentai Generator
Menjana ai hentai secara percuma.

Artikel Panas

Alat panas

Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma

SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan

Hantar Studio 13.0.1
Persekitaran pembangunan bersepadu PHP yang berkuasa

Dreamweaver CS6
Alat pembangunan web visual

SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)

Topik panas
 1378
1378
 52
52
 Panduan ringkas untuk menukar USDT ERC20 kepada TRC20
Jan 18, 2024 pm 06:09 PM
Panduan ringkas untuk menukar USDT ERC20 kepada TRC20
Jan 18, 2024 pm 06:09 PM
Kami mengajar anda langkah demi langkah bagaimana untuk menukar rangkaian USDTERC20 kepada TRC20. Ini kerana ramai orang suka memindahkan stablecoin USDT dari rangkaian Ethereum ke rangkaian Tron untuk menjimatkan yuran transaksi. Jadi, jika anda ingin menukar token ERC-20 anda kepada TRC-20, saya percaya tutorial ini akan membantu anda. Perbezaan antara token ERC-20 dan TRC-20 ERC-20 dan token TRC-20 mewakili token berdasarkan rangkaian Ethereum dan rangkaian Tron masing-masing. Terdapat beberapa perbezaan antara kedua-dua rangkaian, terutamanya dalam aspek berikut: Pertama, rangkaian Ethereum sering menghadapi kesesakan dan bayaran gas yang tinggi, yang boleh menyebabkan kelewatan transaksi dan kos transaksi yang tinggi. Sebagai perbandingan, rangkaian Tron agak kurang sesak
 Petua praktikal untuk menukar huruf Inggeris lebar penuh kepada bentuk separuh lebar
Mar 26, 2024 am 09:54 AM
Petua praktikal untuk menukar huruf Inggeris lebar penuh kepada bentuk separuh lebar
Mar 26, 2024 am 09:54 AM
Petua praktikal untuk menukar huruf Inggeris lebar penuh kepada bentuk separuh lebar Dalam kehidupan moden, kita sering bersentuhan dengan huruf Inggeris, dan kita sering perlu memasukkan huruf Inggeris apabila menggunakan komputer, telefon bimbit dan peranti lain. Walau bagaimanapun, kadangkala kita menemui huruf Inggeris lebar penuh, dan kita perlu menggunakan bentuk separuh lebar. Jadi, bagaimana untuk menukar huruf Inggeris lebar penuh kepada bentuk separuh lebar? Berikut adalah beberapa petua praktikal untuk anda. Pertama sekali, huruf dan nombor Inggeris lebar penuh merujuk kepada aksara yang menduduki kedudukan lebar penuh dalam kaedah input, manakala huruf dan nombor Inggeris separuh lebar menduduki kedudukan lebar penuh.
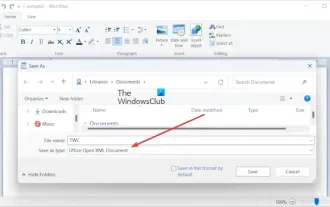 Bagaimana untuk menukar ODT ke Word dalam Windows 11/10?
Feb 20, 2024 pm 12:21 PM
Bagaimana untuk menukar ODT ke Word dalam Windows 11/10?
Feb 20, 2024 pm 12:21 PM
Dalam artikel ini, kami akan menunjukkan kepada anda cara menukar fail OpenDocumentTextDocument (ODT) kepada Microsoft Word (Docx, DOC, dll.). Format. Cara Menukar ODT kepada Word dalam Windows 11/10 Berikut ialah cara anda boleh menukar dokumen ODT kepada format DOC atau DOCX pada Windows PC: Tukar ODT kepada Word menggunakan WordPad atau Word Kaedah pertama yang akan kami tunjukkan kepada anda ialah menggunakan WordPad atau MicrosoftWord untuk menukar ODT kepada Word. Berikut ialah langkah-langkah untuk mencapai ini: Pertama, buka aplikasi WordPad menggunakan menu Mula. Sekarang, pergi ke
 Bagaimana untuk menukar fail AI kepada format CDR
Feb 19, 2024 pm 04:09 PM
Bagaimana untuk menukar fail AI kepada format CDR
Feb 19, 2024 pm 04:09 PM
Fail AI merujuk kepada fail grafik vektor yang dicipta oleh perisian Adobe Illustrator (pendek kata AI), manakala fail CDR merujuk kepada fail grafik vektor yang dicipta oleh perisian CorelDRAW. Memandangkan kedua-dua perisian ini dibangunkan oleh pengeluar yang berbeza, format fail mereka berbeza dan tidak boleh ditukar terus antara satu sama lain. Walau bagaimanapun, kami boleh menukar fail AI kepada fail CDR melalui beberapa kaedah. Kaedah penukaran yang biasa digunakan akan diperkenalkan di bawah. Langkah 1: Eksport fail AI ke format EPS AdobeIllust
 Pemprosesan masa Golang: Cara menukar cap masa kepada rentetan dalam Golang
Feb 24, 2024 pm 10:42 PM
Pemprosesan masa Golang: Cara menukar cap masa kepada rentetan dalam Golang
Feb 24, 2024 pm 10:42 PM
Penukaran masa Golang: Cara menukar cap masa kepada rentetan Di Golang, operasi masa adalah salah satu operasi yang sangat biasa. Kadangkala kita perlu menukar cap masa kepada rentetan untuk paparan atau penyimpanan yang mudah. Artikel ini akan memperkenalkan cara menggunakan Golang untuk menukar cap masa kepada rentetan dan memberikan contoh kod khusus. 1. Penukaran cap masa dan rentetan Di Golang, cap masa biasanya dinyatakan dalam bentuk nombor integer, yang mewakili bilangan saat dari 1 Januari 1970 hingga masa semasa. Rentetannya ialah
 Bagaimana untuk menukar mesin maya kepada mesin fizikal?
Feb 19, 2024 am 11:40 AM
Bagaimana untuk menukar mesin maya kepada mesin fizikal?
Feb 19, 2024 am 11:40 AM
Menukar mesin maya (VM) kepada mesin fizikal ialah proses memindahkan contoh maya dan perisian aplikasi yang berkaitan ke platform perkakasan fizikal. Penukaran ini membantu mengoptimumkan prestasi sistem pengendalian dan penggunaan sumber perkakasan. Artikel ini bertujuan untuk memberikan pandangan yang mendalam tentang cara membuat penukaran ini. Bagaimana untuk melaksanakan migrasi dari mesin maya ke mesin fizikal? Biasanya, proses penukaran antara mesin maya dan mesin fizikal dilakukan di luar mesin maya oleh perisian pihak ketiga. Proses ini terdiri daripada berbilang peringkat yang melibatkan konfigurasi mesin maya dan pemindahan sumber. Sediakan mesin fizikal: Langkah pertama ialah memastikan mesin fizikal memenuhi keperluan perkakasan untuk Windows. Kami perlu membuat sandaran data pada mesin fizikal kerana proses penukaran akan menimpa data sedia ada. *Nama pengguna dan kata laluan untuk akaun pentadbir dengan hak pentadbir untuk mencipta imej sistem. akan menjadi maya
 Penjelasan terperinci tentang kaedah pelaksanaan menukar bulan PHP kepada bulan Inggeris
Mar 21, 2024 pm 06:45 PM
Penjelasan terperinci tentang kaedah pelaksanaan menukar bulan PHP kepada bulan Inggeris
Mar 21, 2024 pm 06:45 PM
Artikel ini akan memperkenalkan secara terperinci cara menukar bulan dalam PHP kepada bulan Inggeris, dan memberikan contoh kod khusus. Dalam pembangunan PHP, kadangkala kita perlu menukar bulan digital kepada bulan Inggeris, yang sangat praktikal dalam beberapa pemprosesan tarikh atau senario paparan data. Prinsip pelaksanaan, contoh kod khusus dan langkah berjaga-jaga akan diterangkan secara terperinci di bawah. 1. Prinsip pelaksanaan Dalam PHP, anda boleh menukar bulan digital kepada bulan Bahasa Inggeris dengan menggunakan kelas DateTime dan kaedah format. Tarikh
 Bagaimana untuk menukar muzik qq kepada format mp3 Tukar muzik qq kepada format mp3 pada telefon mudah alih
Mar 21, 2024 pm 01:21 PM
Bagaimana untuk menukar muzik qq kepada format mp3 Tukar muzik qq kepada format mp3 pada telefon mudah alih
Mar 21, 2024 pm 01:21 PM
QQ Music membolehkan semua orang menikmati menonton filem dan menghilangkan kebosanan Anda boleh menggunakan perisian ini setiap hari untuk memenuhi keperluan anda dengan mudah Sebilangan besar lagu berkualiti tinggi tersedia untuk didengari oleh semua orang Lain kali anda mendengarnya, anda tidak memerlukan sambungan Internet Lagu yang dimuat turun di sini bukan dalam format MP3 dan tidak boleh digunakan pada platform lain Selepas lagu keahlian tamat, tiada cara untuk mendengarnya lagi , ramai rakan ingin menukar lagu ke dalam format MP3 Di sini editornya Anda sediakan kaedah supaya semua orang boleh menggunakannya! 1. Buka QQ Music pada komputer anda, klik butang [Menu Utama] di penjuru kanan sebelah atas, klik [Audio Transcoding], pilih pilihan [Tambah Lagu], dan tambah lagu yang perlu ditukar; lagu, klik untuk memilih Tukar kepada [mp3]



