 pembangunan bahagian belakang
pembangunan bahagian belakang
 C++
C++
 Gunakan penambahan atau penolakan untuk mendapatkan bilangan langkah minimum untuk N pada setiap langkah
Gunakan penambahan atau penolakan untuk mendapatkan bilangan langkah minimum untuk N pada setiap langkah
Gunakan penambahan atau penolakan untuk mendapatkan bilangan langkah minimum untuk N pada setiap langkah
Daripada penyataan masalah di atas, tugas kita adalah untuk mendapatkan bilangan langkah minimum yang mana nombor N yang diberikan boleh diperoleh menggunakan penambahan atau penolakan dalam setiap langkah. Kita boleh memahami bahawa kita perlu mencetak bilangan langkah minimum yang boleh dilakukan dan susunan langkah untuk mana-mana integer N tertentu, dengan menambah dan menolak nombor langkah untuk tiba pada nombor bermula dari 0.
Dalam set masalah ini, kita boleh menambah atau menolak nombor yang sama dengan bilangan langkah ke kedudukan semasa pada setiap langkah. Sebagai contoh, kita boleh menambah 1 atau -1 dalam langkah 1. Selanjutnya kita boleh menambah 2 atau -2 dalam langkah 2 dan seterusnya. Kita boleh menambah atau menolak nombor pada setiap langkah bergantung pada keadaan.
Cabaran utama masalah ini ialah kita perlu melakukan bilangan langkah minimum bermula dari 0 untuk mencapai N. Marilah kita memahami isu ini dengan lebih baik dengan contoh.
Contoh yang diberikan di bawah akan menunjukkan kepada anda setiap nombor yang kami dapat dalam 2 langkah bermula dari 0 dengan melakukan operasi di atas.
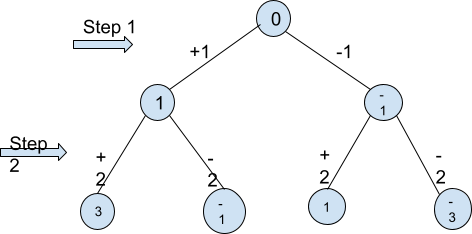
Sebagai contoh, andaikan kita mempunyai N=1.
Output
Minimum no of steps: 1 Sequence of steps: 1
Penerangan
Kita boleh mencapai 1 dalam dua cara -
Hanya tambahkan 1 kepada langkah 1 untuk beralih dari 0 kepada 1, yang mengambil 1 langkah.
Tolak 1 dalam langkah 1 untuk bergerak dari 0 kepada -1, kemudian tambah 2 dalam langkah 2 untuk beralih dari -1 kepada 1, yang mengambil 2 langkah.
Oleh kerana masalah menyatakan bahawa kita memerlukan bilangan langkah minimum untuk mencapai sebarang nombor N, output yang dikehendaki untuk input ini ialah 1.
Untuk, N=3
Output
Minimum no of steps: 2 Sequence of steps: 1 2
Penerangan
Kami menambah 1 dalam langkah 1 untuk beralih dari 0 kepada 1, kemudian menambah 2 dalam langkah 2 untuk beralih dari 1 kepada 3.
kaedah
Cara terbaik untuk menyelesaikan masalah adalah dengan terlebih dahulu mengetahui sama ada N ialah nombor positif atau negatif. Kita mesti menambah atau menolak bilangan langkah yang sesuai masing-masing untuk menyelesaikan masalah.
Jika N ialah nombor positif, teruskan menambah langkah sehingga jumlahnya lebih besar daripada atau sama dengan N.
Begitu juga, jika N ialah nombor negatif, teruskan menolak bilangan langkah sehingga jumlahnya lebih besar daripada atau sama dengan N.
Jika jumlahnya sama dengan N dalam kes di atas, kembalikan bilangan langkah dan susunan langkah. Masalah utama ialah mengendalikan situasi apabila N melebihi.
Setelah jumlah melebihi N, semak sama ada (jumlah-N) genap atau ganjil.
Jika (jumlah-N) genap, maka kita perlu melakukan penolakan dalam langkah (jumlah-N)/2 untuk mencapai N.
Marilah kita memahami kes ini dengan lebih baik melalui contoh yang sesuai.
Untuk, N=8
1+2+3+4=10, iaitu lebih daripada 8.
Kerana 10-8=2 ialah nombor genap. Jadi kita akan tolak dalam langkah 2/2, iaitu
Langkah 1. Oleh itu, susunan langkahnya ialah -1 2 3 4 dan minimum
Bilangan langkah untuk mencapai N ialah 4.
Jika (jumlah-N) ialah nombor ganjil, mula-mula tentukan sama ada nombor yang jumlahnya melebihi N dalam langkah sebelumnya adalah genap atau ganjil.
Jika langkah sebelumnya adalah ganjil, maka lakukan langkah dengan menambah nombor langkah seterusnya yang akan menjadikan (jumlah-N) kita genap dan kemudian lakukan langkah di atas untuk mendapatkan hasil yang diinginkan.
Sebagai contoh, N=9
1+2+3+4=10, iaitu lebih daripada 9.
Oleh kerana 10-9=1, ini adalah nombor ganjil. Langkah seterusnya ialah 5, iaitu nombor ganjil, jadi kita hanya melakukan satu langkah dan menambah 5 kepada jumlah untuk mendapatkan 15, menjadikan (jumlah-N)=6. Melakukan penolakan dalam langkah 3 akan memberikan anda urutan 1 2 -3 4 5, iaitu output yang diingini.
Andaikan langkah sebelumnya ialah nombor genap Dalam kes ini, kita perlu melakukan dua langkah, tambah langkah ke-i dan tolak langkah (i+1) untuk mendapatkan. (jumlah - N) sebagai nombor genap untuk mendapatkan urutan langkah yang dikehendaki.
untuk N=5
1+2+3=6, lebih daripada 5.
Oleh kerana (jumlah-N) =1, kami akan mempertimbangkan langkah terakhir apabila su melebihi nombor N. Oleh kerana ia adalah nombor genap, kami akan melakukan dua langkah, langkah 4 dan langkah 5. Tugas kita adalah untuk membuat (jumlah-N) walaupun begitu, dengan menambah dalam langkah 4 dan menolak dalam langkah 5 kita boleh membuat (jumlah-N) walaupun 1 ditolak daripada jumlah. Oleh kerana (jumlah-N) sama dengan 0, kita mendapat N. Oleh itu, urutannya ialah 1 2 3 4 -5.
Contoh
Berikut ialah kod C++ kaedah ini -
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
void minimumStep(int n){
vector <int> steps; // for storing the sequence
int totalSum=0;
int temp=0;
if(n>=0){ // if n is positive then temp will store positive
temp=1;
} else {
temp=-1; // n is negative then temp will store negative
}
n=abs(n);
int step=0;
for(step=1;totalSum<n;step++){ // for storing the steps till sum is not greater than n
steps.push_back(temp*step);
totalSum=totalSum+step;
}
if(totalSum>temp*n) { //when sum greater than n
if(step%2==0) { //when step is even
totalSum=totalSum-n;
if((totalSum)%2!=0) { // when totalSum-n is odd
steps.push_back(temp*step); //store the addition of next step
steps.push_back((temp*-1)*(step+1)); // store the subtraction of next step
totalSum--; //make totalSum even
}
int check=(totalSum)/2;
check--;
steps[check]=steps[check]*-1;
} else { //when step is odd
totalSum=totalSum-n;
if((totalSum)%2!=0) { // when totalSum-n is odd
steps.push_back(temp*step); //store the next addition value
totalSum+=step;
step++;
}
int check=(totalSum)/2;
check--;
steps[check]=steps[check]*-1;
}
}
//print the minimum number of steps taken
cout<<"The minimum number of steps : "<<steps.size()<<endl;
//print the steps is stored in vector
cout<<"Sequence of steps : ";
for(int i=0;i<steps.size();i++){
cout<<steps[i]<<" ";
}
}
int main(){
int m=17;
minimumStep(m);
return 0;
}
Output
The minimum number of steps : 6 Sequence of steps : 1 -2 3 4 5 6
Kerumitan masa: O(sqrt(N))
Kerumitan ruang: O(sqrt(N))
KESIMPULAN
Dalam artikel ini, kami cuba menerangkan kaedah untuk mencari bilangan langkah minimum untuk mencapai N dengan menambah atau menolak pada setiap langkah dan mencetak jujukan. Saya harap artikel ini membantu anda mempelajari konsep ini dengan lebih baik.
Atas ialah kandungan terperinci Gunakan penambahan atau penolakan untuk mendapatkan bilangan langkah minimum untuk N pada setiap langkah. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

Video Face Swap
Tukar muka dalam mana-mana video dengan mudah menggunakan alat tukar muka AI percuma kami!

Artikel Panas

Alat panas

Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma

SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan

Hantar Studio 13.0.1
Persekitaran pembangunan bersepadu PHP yang berkuasa

Dreamweaver CS6
Alat pembangunan web visual

SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)

Topik panas
 1658
1658
 14
14
 1415
1415
 52
52
 1309
1309
 25
25
 1257
1257
 29
29
 1231
1231
 24
24
 Cara menulis kod tambahan Python_Tutorial menulis kod tambahan Python
Apr 02, 2024 pm 06:16 PM
Cara menulis kod tambahan Python_Tutorial menulis kod tambahan Python
Apr 02, 2024 pm 06:16 PM
1. Mula-mula buka halaman suntingan python dalam talian. 2. Kemudian masukkan kod program di kawasan program. 3. Kemudian klik Jalankan di sudut kiri atas, masukkan addend pertama, tekan Enter, dan masukkan addend kedua. 4. Akhir sekali tekan Enter untuk mendapatkan jumlah dua tambahan. Ini adalah kod tambahan python yang mudah.
 Bahagi dua integer tanpa menggunakan pengendali pendaraban, pembahagian dan modulo
Sep 21, 2023 pm 12:41 PM
Bahagi dua integer tanpa menggunakan pengendali pendaraban, pembahagian dan modulo
Sep 21, 2023 pm 12:41 PM
Dalam masalah ini, kita hanya perlu membahagi dua integer tanpa menggunakan operator darab, bahagi dan modulo. Walaupun kita boleh menggunakan operasi tambah, darab atau bit. Pernyataan masalah menyatakan bahawa kita akan mendapat dua integer x dan y. Tanpa menggunakan pendaraban, pembahagian, atau operator modulo, kita perlu menentukan hasil bagi x dibahagikan dengan y. Contoh Input: x=15, y=5 Output: 3 Input: x=10, y=4 Output: 2 Input: x=-20, y=3 Output: -6 Kaedah Kaedah 1 (gunakan matematik mudah) di sini Dalam ini kaedah, kami akan menggunakan algoritma matematik yang mudah. Berikut ialah penjelasan langkah demi langkah tentang langkah yang akan kami ikuti - kami akan terus menolak pembahagi (iaitu y) daripada dividen (iaitu x) sehingga x lebih besar daripada atau sama dengan y. apabila y lebih besar daripada x
 Kemahiran operasi pangkalan data Oracle: penerangan terperinci tentang operasi tolak
Mar 02, 2024 pm 06:15 PM
Kemahiran operasi pangkalan data Oracle: penerangan terperinci tentang operasi tolak
Mar 02, 2024 pm 06:15 PM
Sebagai sistem pengurusan pangkalan data hubungan yang berkuasa, pangkalan data Oracle menyediakan banyak operasi pengkomputeran untuk memenuhi keperluan pengguna. Dalam operasi pangkalan data harian, operasi penolakan adalah operasi biasa dan penting. Ia boleh membantu kami merealisasikan operasi penolakan data untuk mendapatkan hasil yang kami perlukan. Artikel ini akan membincangkan secara terperinci teknik yang berkaitan dengan operasi penolakan dalam pangkalan data Oracle, dan memberikan contoh kod khusus untuk membantu pembaca memahami dan menggunakan fungsi ini dengan lebih baik. 1. Konsep asas operasi tolak dalam data Oracle
 Bagaimana untuk melakukan penolakan dalam Excel
Mar 20, 2024 pm 02:46 PM
Bagaimana untuk melakukan penolakan dalam Excel
Mar 20, 2024 pm 02:46 PM
Excel ialah perisian pejabat yang sangat diperlukan di pejabat harian kami, jadi bagi sesetengah orang yang pertama kali belajar Excel, mereka akan sentiasa menghadapi beberapa masalah kecil, seperti cara melakukan penolakan dalam Excel Hari ini saya akan bercakap dengan rakan saya Kongsi ini langkah operasi. 1. Pertama, buka helaian data Excel Excel ingin melakukan penolakan melalui formula, dan formula secara amnya berpandukan tanda sama, jadi dalam sel yang perlu ditolak, mula-mula masukkan =, (seperti yang ditunjukkan dalam warna merah di bawah) Bulatkan. bahagian ditunjukkan). 2. Kemudian, klik pada sel di mana minuend terletak, dan nama sel akan ditambah secara automatik pada formula (seperti yang ditunjukkan dalam bulatan merah dalam rajah di bawah). 3
 Terokai maksud dan aplikasi pengendali Python: penambahan, penolakan, pendaraban dan pembahagian
Jan 20, 2024 am 09:21 AM
Terokai maksud dan aplikasi pengendali Python: penambahan, penolakan, pendaraban dan pembahagian
Jan 20, 2024 am 09:21 AM
Pemahaman mendalam tentang pengendali Python: penambahan, penolakan, pendaraban, pembahagian dan maksudnya memerlukan contoh kod khusus Dalam bahasa pengaturcaraan Python, operator adalah salah satu alat penting untuk melaksanakan pelbagai operasi matematik. Antaranya, penambahan, penolakan, pendaraban dan pembahagian adalah operator yang paling biasa Artikel ini akan menyelidiki maksud operator ini dan cara menggunakannya dalam Python. Operator Penambahan (+) Operator tambah digunakan untuk menambah dua nombor dan juga boleh digunakan untuk menggabungkan dua rentetan. x=5y=3hasil
 Cara membuat reka bentuk tolak dan mencantikkan carta dalam PPT
Mar 20, 2024 pm 02:00 PM
Cara membuat reka bentuk tolak dan mencantikkan carta dalam PPT
Mar 20, 2024 pm 02:00 PM
1. Ruang operasi pengindahan asas carta adalah kecil, dan elemen paparan yang mengganggu dialih keluar. Elemen yang mengganggu data termasuk latar belakang, garis grid dan legenda, yang boleh dipadamkan, dicantikkan dan bayang-bayang dilembutkan. 2. Masukkan [PPT], [Buka] carta, klik [Carta], pilih [+], dan nyahtanda [tanda]nya, seperti yang ditunjukkan dalam rajah. 3. [Klik kanan] untuk menetapkan format siri data, klik [Isi], dan tandakan [Tiada Isi]. Klik [Lajur Data], klik [Bayang] untuk mengalih keluar bayang-bayang, pilih [Kerangka] dan warnakan [Teks] putih. 4. Klik [Skala], pilih [Tanda Skala], laraskan [Jenis Tema] Tiada, [Warna] putih, seperti yang ditunjukkan dalam rajah. 5. Padamkan tempat-tempat yang perlu dipadamkan untuk menjadikan jadual lebih jelas Jangan menambah perkara secara membabi buta semasa mereka bentuk, lakukan dengan sewajarnya.
 Gunakan pthread untuk melaksanakan penambahan dan penolakan matriks dalam C/C++
Aug 28, 2023 am 09:05 AM
Gunakan pthread untuk melaksanakan penambahan dan penolakan matriks dalam C/C++
Aug 28, 2023 am 09:05 AM
Di sini kita akan melihat cara melakukan penambahan dan penolakan matriks menggunakan persekitaran berbilang benang. pthread digunakan untuk melaksanakan berbilang benang secara serentak dalam C atau C++. Terdapat dua matriks A dan B. Susunan setiap matriks ialah (mxn). Setiap benang akan mendapat setiap baris dan melakukan penambahan atau penolakan. Jadi, untuk m baris, terdapat m benang yang berbeza. Contoh#include<iostream>#include<pthread.h>#include<cstdlib>#include<cstdint>#defineCORE3#defineMAX3usingnamespacestd;i
 Mengapa membahagikan 8 dengan -3 dalam PHP menghasilkan 0?
Jan 26, 2024 am 10:36 AM
Mengapa membahagikan 8 dengan -3 dalam PHP menghasilkan 0?
Jan 26, 2024 am 10:36 AM
Mengapakah PHP8%-3 sama dengan 0? Dalam pengaturcaraan PHP, kadangkala kita menghadapi beberapa masalah yang pelik dan mengelirukan. Soalan yang sangat menarik ialah, mengapa ungkapan 8%-3 dalam PHP sama dengan 0? Untuk menjawab soalan ini, pertama kita perlu memahami operasi modular (operasi baki) dalam PHP. Aritmetik modulo ialah operasi matematik yang digunakan untuk mengira baki selepas membahagi satu nombor dengan yang lain. Dalam PHP, tanda peratus (%) digunakan untuk mewakili aritmetik modular. Dalam matematik, apabila satu nombor dibahagikan dengan nombor lain dan bakinya ialah 0, kita katakan itu



