 hujung hadapan web
hujung hadapan web
 tutorial js
tutorial js
 Program JavaScript menyemak sama ada semua elemen tatasusunan boleh ditukar kepada nombor pronik dengan memutar nombor
Program JavaScript menyemak sama ada semua elemen tatasusunan boleh ditukar kepada nombor pronik dengan memutar nombor
Program JavaScript menyemak sama ada semua elemen tatasusunan boleh ditukar kepada nombor pronik dengan memutar nombor

Nombor Plonik juga dipanggil nombor segi empat tepat ialah gandaan dua nombor berturut-turut. Kami akan mendapat tatasusunan integer dan kami boleh memutar nombor ke mana-mana arah beberapa kali untuk mendapatkan semua kombinasi. Untuk sebarang kombinasi yang dihasilkan dengan memutar nombor, jika setiap elemen tatasusunan boleh ditukar kepada nombor Plonik, maka kami akan mencetak benar, jika tidak kami akan mencetak palsu.
Nombor Pronik
Pertama, mari kita bincangkan nombor proton: Nombor proton ialah hasil darab dua nombor berturut-turut.
Secara matematik, jika kita mempunyai integer x yang nombor berturut-turutnya ialah x+1, dan biarkan nombor k adalah hasil darab kedua-duanya, ini bermakna: k = (x)*(x+1). Beberapa contoh nombor Pronik ialah:
0 ialah hasil daripada 0 dan 1.
1 ialah produk 1 dan 2.
6 ialah hasil daripada 2 dan 3.
-> 12, 20, 30, 42, 56, 72, 90, 110, 132, 156, 182, 210, 240, 272, dsb.
Contoh
Katakan kita mempunyai tatasusunan:
{ 21, 65, 227, 204, 2}
Output: Ya
Penerangan:
Untuk indeks sifar: 21, satu putaran bertukar kepada 12, iaitu hasil darab 3 dan 4, maka nombor Planck.
Untuk indeks pertama: 65, selepas satu putaran ia boleh ditukar kepada 56, iaitu hasil darab 7 dan 8 dan oleh itu nombor Plonik.
Untuk indeks kedua: 227, ia boleh ditukar kepada 272 selepas satu putaran, iaitu nombor pronik.
Begitu juga, 204 hingga 420 dan 2 itu sendiri adalah nombor proton.
Kaedah
Kami telah melihat contoh kod, sekarang mari kita masuk ke langkah -
Pertama, kami akan mentakrifkan fungsi untuk memutar nombor yang diberikan. Integer akan dihantar sebagai hujah dan akan ditukar kepada rentetan.
Menggunakan kaedah subrentetan, kami memutarkan rentetan ke kanan dan kemudian menukarnya kembali kepada nombor sekali lagi dan ke belakang.
Kami akan mentakrifkan fungsi pronik untuk menyemak sama ada nombor semasa adalah pronik.
Kita akan mencari sempadan bawah punca kuasa dua nombor semasa dan mendarabkannya dengan nombor berturut-turut untuk menentukan sama ada nombor semasa ialah proton.
Kami akan mentakrifkan fungsi untuk mencari bilangan digit dalam nombor semasa dengan menukarnya kepada rentetan.
Dalam fungsi utama kita akan melelar melalui tatasusunan dan untuk setiap elemen kita akan memutarkannya mengikut panjangnya atau sehingga kita menemui nombor Pronik.
Jika kami menemui sebarang nombor selepas semua lelaran yang bukan nombor pronik dan kami tidak boleh menukarnya kepada nombor pronik, maka kami tidak akan mencetak ya.
Contoh
Dalam contoh di bawah, kami menyemak sama ada semua elemen tatasusunan boleh ditukar kepada nombor Plonik dengan memutar nombor. Input dan output yang dijangka diberikan di bawah.
Input: tatasusunan = [21, 65, 227, 204, 2]
Output yang dijangkakan: Ya
// function to rotate the digits
function rotate(num){
// converting integer to string
var str = num.toString();
// putting first index value to last
str = str.substring(1) + str.substring(0,1);
// converting back string to integer
num = parseInt(str);
return num;
}
// function to check whether current number if pronic number or not
function isPronic(num){
// getting square root of the current number
var cur = Math.sqrt(num);
// taking floor of cur
cur = Math.floor(cur);
if(cur*(cur+1) == num) {
return true;
}
else {
return false;
}
}
// function to find the length of the current integer
function number_length(num){
var str = num.toString()
var len = str.length;
return len;
}
// function to check whether array is pronic or not
function check(arr){
var len = arr.length;
for(var i =0; i<len; i++){
// getting length of the current number
var cur = number_length(arr[i]);
while(cur--){
if(isPronic(arr[i])){
break;
}
arr[i] = rotate(arr[i]);
}
if(isPronic(arr[i]) == false){
return false;
}
}
return true;
}
var arr = [21, 65, 227, 204, 2]
console.log("Array:", JSON.stringify(arr))
if(check(arr)){
console.log("The elements of array can be converted to pronic numbers.");
}
else{
console.log("The elements of array can't be converted to pronic numbers.");
}
Output
Array: [21,65,227,204,2] The elements of array can be converted to pronic numbers.
Kerumitan masa dan ruang
Kerumitan masa kod di atas ialah O(N), dengan N ialah saiz tatasusunan. Di sini kita mendapat faktor logaritma bersaiz nombor tambahan untuk menggelung ke atas tatasusunan dan mengambil punca kuasa duanya, tetapi memandangkan panjang maksimum integer tertentu adalah sangat kecil, tiada kesan pada kerumitan masa linear.
Kerumitan ruang kod di atas adalah malar atau O(1) kerana kami tidak menggunakan sebarang ruang tambahan di sini.
Kesimpulan
Dalam tutorial ini kami telah melaksanakan program JavaScript untuk mencari cuaca dengan menukar setiap elemen tatasusunan kepada nombor pronik hanya dengan memutarkan nombornya ke kiri atau kanan. Kami menentukan beberapa fungsi untuk memutar nombor, menyemak sama ada ia adalah proton dan mendapatkan bilangan digit. Kerumitan masa kod di atas ialah O(N) dan kerumitan ruang ialah O(1).
Atas ialah kandungan terperinci Program JavaScript menyemak sama ada semua elemen tatasusunan boleh ditukar kepada nombor pronik dengan memutar nombor. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

AI Hentai Generator
Menjana ai hentai secara percuma.

Artikel Panas

Alat panas

Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma

SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan

Hantar Studio 13.0.1
Persekitaran pembangunan bersepadu PHP yang berkuasa

Dreamweaver CS6
Alat pembangunan web visual

SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)

Topik panas
 Ganti aksara rentetan dalam javascript
Mar 11, 2025 am 12:07 AM
Ganti aksara rentetan dalam javascript
Mar 11, 2025 am 12:07 AM
Penjelasan terperinci mengenai kaedah penggantian rentetan javascript dan Soalan Lazim Artikel ini akan meneroka dua cara untuk menggantikan watak rentetan dalam JavaScript: Kod JavaScript dalaman dan HTML dalaman untuk laman web. Ganti rentetan di dalam kod JavaScript Cara yang paling langsung ialah menggunakan kaedah pengganti (): str = str.replace ("cari", "ganti"); Kaedah ini hanya menggantikan perlawanan pertama. Untuk menggantikan semua perlawanan, gunakan ungkapan biasa dan tambahkan bendera global g: str = str.replace (/fi
 Tutorial Persediaan API Carian Google Custom
Mar 04, 2025 am 01:06 AM
Tutorial Persediaan API Carian Google Custom
Mar 04, 2025 am 01:06 AM
Tutorial ini menunjukkan kepada anda bagaimana untuk mengintegrasikan API carian Google tersuai ke dalam blog atau laman web anda, menawarkan pengalaman carian yang lebih halus daripada fungsi carian tema WordPress standard. Ia menghairankan mudah! Anda akan dapat menyekat carian ke y
 Contoh warna json fail
Mar 03, 2025 am 12:35 AM
Contoh warna json fail
Mar 03, 2025 am 12:35 AM
Siri artikel ini ditulis semula pada pertengahan 2017 dengan maklumat terkini dan contoh segar. Dalam contoh JSON ini, kita akan melihat bagaimana kita dapat menyimpan nilai mudah dalam fail menggunakan format JSON. Menggunakan notasi pasangan nilai utama, kami boleh menyimpan apa-apa jenis
 Bina Aplikasi Web Ajax anda sendiri
Mar 09, 2025 am 12:11 AM
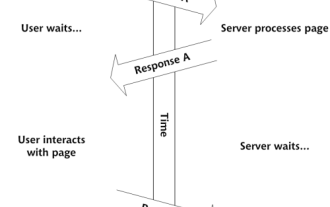
Bina Aplikasi Web Ajax anda sendiri
Mar 09, 2025 am 12:11 AM
Jadi di sini anda, bersedia untuk mempelajari semua perkara ini yang dipanggil Ajax. Tetapi, apa sebenarnya? Istilah Ajax merujuk kepada kumpulan teknologi longgar yang digunakan untuk membuat kandungan web yang dinamik dan interaktif. Istilah Ajax, yang asalnya dicipta oleh Jesse J
 10 JQuery Syntax Highlighters
Mar 02, 2025 am 12:32 AM
10 JQuery Syntax Highlighters
Mar 02, 2025 am 12:32 AM
Tingkatkan Penyampaian Kod Anda: 10 Penyeret Sintaks untuk Pemaju Coretan kod perkongsian di laman web atau blog anda adalah amalan biasa bagi pemaju. Memilih penyapu sintaks yang betul dapat meningkatkan daya tarikan dan daya tarikan visual dengan ketara. T
 8 plugin susun atur halaman jquery yang menakjubkan
Mar 06, 2025 am 12:48 AM
8 plugin susun atur halaman jquery yang menakjubkan
Mar 06, 2025 am 12:48 AM
Leverage JQuery untuk Layouts Laman Web yang mudah: 8 Plugin Essential JQuery memudahkan susun atur laman web dengan ketara. Artikel ini menyoroti lapan plugin jQuery yang kuat yang menyelaraskan proses, terutamanya berguna untuk penciptaan laman web manual
 Apa itu ' ini ' Dalam JavaScript?
Mar 04, 2025 am 01:15 AM
Apa itu ' ini ' Dalam JavaScript?
Mar 04, 2025 am 01:15 AM
Mata teras Ini dalam JavaScript biasanya merujuk kepada objek yang "memiliki" kaedah, tetapi ia bergantung kepada bagaimana fungsi dipanggil. Apabila tidak ada objek semasa, ini merujuk kepada objek global. Dalam penyemak imbas web, ia diwakili oleh tetingkap. Apabila memanggil fungsi, ini mengekalkan objek global; tetapi apabila memanggil pembina objek atau mana -mana kaedahnya, ini merujuk kepada contoh objek. Anda boleh mengubah konteks ini menggunakan kaedah seperti panggilan (), memohon (), dan mengikat (). Kaedah ini memanggil fungsi menggunakan nilai dan parameter yang diberikan. JavaScript adalah bahasa pengaturcaraan yang sangat baik. Beberapa tahun yang lalu, ayat ini
 10 JavaScript & JQuery MVC Tutorial
Mar 02, 2025 am 01:16 AM
10 JavaScript & JQuery MVC Tutorial
Mar 02, 2025 am 01:16 AM
Artikel ini membentangkan pemilihan lebih daripada 10 tutorial mengenai rangka kerja javascript dan jquery model-view-controller (MVC), sesuai untuk meningkatkan kemahiran pembangunan web anda pada tahun baru. Tutorial ini merangkumi pelbagai topik, dari Foundatio





