Cara menggunakan java untuk melaksanakan algoritma titik potong graf

Cara menggunakan java untuk melaksanakan algoritma titik potong graf memerlukan contoh kod khusus
Graf adalah salah satu konsep penting dalam diskret matematik, melalui perwakilan Graf boleh menerangkan hubungan dan perkaitan yang muncul dalam pelbagai masalah dunia sebenar. Dalam algoritma berkaitan graf, mencari titik potong graf adalah masalah yang mencabar. Titik potong graf juga dipanggil titik sambungan atau bahagian atas potong Ia bermaksud bahawa dalam graf bersambung tidak berarah, jika bucu dan semua tepi yang berkaitan dengan bucu dibuang, graf asal tidak lagi bersambung dipanggil titik potong.
Artikel ini akan memperkenalkan cara menggunakan bahasa pengaturcaraan Java untuk melaksanakan algoritma titik potong graf dan memberikan contoh kod khusus. Pertama, kita perlu mentakrifkan struktur data graf Berikut ialah contoh kelas graf ringkas:
import java.util.*;
class Graph {
private int V; // 顶点的数量
private LinkedList<Integer> adj[]; // 邻接表形式的图
// 构造函数,初始化图
Graph(int v) {
V = v;
adj = new LinkedList[v];
for (int i=0; i<v; ++i)
adj[i] = new LinkedList();
}
// 添加边到图中
void addEdge(int v, int w) {
adj[v].add(w);
adj[w].add(v);
}
// 递归函数,实现割点算法
void cutVertexUtil(int u, boolean visited[], int disc[], int low[], int parent[], boolean ap[]) {
int children = 0;
visited[u] = true;
disc[u] = low[u] = ++time;
Iterator<Integer> i = adj[u].iterator();
while (i.hasNext()) {
int v = i.next();
if (!visited[v]) {
children++;
parent[v] = u;
cutVertexUtil(v, visited, disc, low, parent, ap);
low[u] = Math.min(low[u], low[v]);
if (parent[u] == -1 && children > 1)
ap[u] = true;
if (parent[u] != -1 && low[v] >= disc[u])
ap[u] = true;
}
else if (v != parent[u])
low[u] = Math.min(low[u], disc[v]);
}
}
// 割点算法的主函数
void cutVertices() {
boolean visited[] = new boolean[V];
int disc[] = new int[V];
int low[] = new int[V];
int parent[] = new int[V];
boolean ap[] = new boolean[V]; // 记录割点
for (int i = 0; i < V; i++) {
parent[i] = -1;
visited[i] = false;
ap[i] = false;
}
for (int i = 0; i < V; i++)
if (visited[i] == false)
cutVertexUtil(i, visited, disc, low, parent, ap);
System.out.println("割点:");
for (int i = 0; i < V; i++)
if (ap[i] == true)
System.out.print(i+" ");
System.out.println();
}
public static void main(String args[]) {
Graph g1 = new Graph(5);
g1.addEdge(1, 0);
g1.addEdge(0, 2);
g1.addEdge(2, 1);
g1.addEdge(0, 3);
g1.addEdge(3, 4);
System.out.println("以下是图g1中的割点:");
g1.cutVertices();
Graph g2 = new Graph(4);
g2.addEdge(0, 1);
g2.addEdge(1, 2);
g2.addEdge(2, 3);
System.out.println("以下是图g2中的割点:");
g2.cutVertices();
Graph g3 = new Graph(7);
g3.addEdge(0, 1);
g3.addEdge(1, 2);
g3.addEdge(2, 0);
g3.addEdge(1, 3);
g3.addEdge(1, 4);
g3.addEdge(1, 6);
g3.addEdge(3, 5);
g3.addEdge(4, 5);
System.out.println("以下是图g3中的割点:");
g3.cutVertices();
}
}Dalam contoh kod ini, kami mencipta kelas Graf untuk mewakili graf, menggunakan bentuk satu senarai bersebelahan untuk menyimpan tepi graf. Dalam pelaksanaan algoritma titik potong, kami menggunakan kaedah traversal carian mendalam-pertama dan menggunakan beberapa tatasusunan tambahan untuk merekodkan status akses, masa penemuan, nod nenek moyang yang paling awal dilawati dan menandakan titik potong. Dengan memanggil fungsi cutVertices(), anda boleh mencari titik potong dalam graf dan mengeluarkan indeks titik potong. cutVertices()函数,可以找到图中的割点,并输出割点的索引。
代码示例中的main
Atas ialah kandungan terperinci Cara menggunakan java untuk melaksanakan algoritma titik potong graf. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

AI Hentai Generator
Menjana ai hentai secara percuma.

Artikel Panas

Alat panas

Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma

SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan

Hantar Studio 13.0.1
Persekitaran pembangunan bersepadu PHP yang berkuasa

Dreamweaver CS6
Alat pembangunan web visual

SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)

Topik panas
 1377
1377
 52
52
 CLIP-BEVFormer: Selia secara eksplisit struktur BEVFormer untuk meningkatkan prestasi pengesanan ekor panjang
Mar 26, 2024 pm 12:41 PM
CLIP-BEVFormer: Selia secara eksplisit struktur BEVFormer untuk meningkatkan prestasi pengesanan ekor panjang
Mar 26, 2024 pm 12:41 PM
Ditulis di atas & pemahaman peribadi penulis: Pada masa ini, dalam keseluruhan sistem pemanduan autonomi, modul persepsi memainkan peranan penting Hanya selepas kenderaan pemanduan autonomi yang memandu di jalan raya memperoleh keputusan persepsi yang tepat melalui modul persepsi boleh Peraturan hiliran dan. modul kawalan dalam sistem pemanduan autonomi membuat pertimbangan dan keputusan tingkah laku yang tepat pada masanya dan betul. Pada masa ini, kereta dengan fungsi pemanduan autonomi biasanya dilengkapi dengan pelbagai penderia maklumat data termasuk penderia kamera pandangan sekeliling, penderia lidar dan penderia radar gelombang milimeter untuk mengumpul maklumat dalam modaliti yang berbeza untuk mencapai tugas persepsi yang tepat. Algoritma persepsi BEV berdasarkan penglihatan tulen digemari oleh industri kerana kos perkakasannya yang rendah dan penggunaan mudah, dan hasil keluarannya boleh digunakan dengan mudah untuk pelbagai tugas hiliran.
 Melaksanakan Algoritma Pembelajaran Mesin dalam C++: Cabaran dan Penyelesaian Biasa
Jun 03, 2024 pm 01:25 PM
Melaksanakan Algoritma Pembelajaran Mesin dalam C++: Cabaran dan Penyelesaian Biasa
Jun 03, 2024 pm 01:25 PM
Cabaran biasa yang dihadapi oleh algoritma pembelajaran mesin dalam C++ termasuk pengurusan memori, multi-threading, pengoptimuman prestasi dan kebolehselenggaraan. Penyelesaian termasuk menggunakan penunjuk pintar, perpustakaan benang moden, arahan SIMD dan perpustakaan pihak ketiga, serta mengikuti garis panduan gaya pengekodan dan menggunakan alat automasi. Kes praktikal menunjukkan cara menggunakan perpustakaan Eigen untuk melaksanakan algoritma regresi linear, mengurus memori dengan berkesan dan menggunakan operasi matriks berprestasi tinggi.
 Terokai prinsip asas dan pemilihan algoritma bagi fungsi isihan C++
Apr 02, 2024 pm 05:36 PM
Terokai prinsip asas dan pemilihan algoritma bagi fungsi isihan C++
Apr 02, 2024 pm 05:36 PM
Lapisan bawah fungsi C++ sort menggunakan isihan gabungan, kerumitannya ialah O(nlogn), dan menyediakan pilihan algoritma pengisihan yang berbeza, termasuk isihan pantas, isihan timbunan dan isihan stabil.
 Bolehkah kecerdasan buatan meramalkan jenayah? Terokai keupayaan CrimeGPT
Mar 22, 2024 pm 10:10 PM
Bolehkah kecerdasan buatan meramalkan jenayah? Terokai keupayaan CrimeGPT
Mar 22, 2024 pm 10:10 PM
Konvergensi kecerdasan buatan (AI) dan penguatkuasaan undang-undang membuka kemungkinan baharu untuk pencegahan dan pengesanan jenayah. Keupayaan ramalan kecerdasan buatan digunakan secara meluas dalam sistem seperti CrimeGPT (Teknologi Ramalan Jenayah) untuk meramal aktiviti jenayah. Artikel ini meneroka potensi kecerdasan buatan dalam ramalan jenayah, aplikasi semasanya, cabaran yang dihadapinya dan kemungkinan implikasi etika teknologi tersebut. Kecerdasan Buatan dan Ramalan Jenayah: Asas CrimeGPT menggunakan algoritma pembelajaran mesin untuk menganalisis set data yang besar, mengenal pasti corak yang boleh meramalkan di mana dan bila jenayah mungkin berlaku. Set data ini termasuk statistik jenayah sejarah, maklumat demografi, penunjuk ekonomi, corak cuaca dan banyak lagi. Dengan mengenal pasti trend yang mungkin terlepas oleh penganalisis manusia, kecerdasan buatan boleh memperkasakan agensi penguatkuasaan undang-undang
 Algoritma pengesanan yang dipertingkatkan: untuk pengesanan sasaran dalam imej penderiaan jauh optik resolusi tinggi
Jun 06, 2024 pm 12:33 PM
Algoritma pengesanan yang dipertingkatkan: untuk pengesanan sasaran dalam imej penderiaan jauh optik resolusi tinggi
Jun 06, 2024 pm 12:33 PM
01Garis prospek Pada masa ini, sukar untuk mencapai keseimbangan yang sesuai antara kecekapan pengesanan dan hasil pengesanan. Kami telah membangunkan algoritma YOLOv5 yang dipertingkatkan untuk pengesanan sasaran dalam imej penderiaan jauh optik resolusi tinggi, menggunakan piramid ciri berbilang lapisan, strategi kepala pengesanan berbilang dan modul perhatian hibrid untuk meningkatkan kesan rangkaian pengesanan sasaran dalam imej penderiaan jauh optik. Menurut set data SIMD, peta algoritma baharu adalah 2.2% lebih baik daripada YOLOv5 dan 8.48% lebih baik daripada YOLOX, mencapai keseimbangan yang lebih baik antara hasil pengesanan dan kelajuan. 02 Latar Belakang & Motivasi Dengan perkembangan pesat teknologi penderiaan jauh, imej penderiaan jauh optik resolusi tinggi telah digunakan untuk menggambarkan banyak objek di permukaan bumi, termasuk pesawat, kereta, bangunan, dll. Pengesanan objek dalam tafsiran imej penderiaan jauh
 Amalkan dan fikirkan platform model besar berbilang modal Jiuzhang Yunji DataCanvas
Oct 20, 2023 am 08:45 AM
Amalkan dan fikirkan platform model besar berbilang modal Jiuzhang Yunji DataCanvas
Oct 20, 2023 am 08:45 AM
1. Perkembangan sejarah model besar pelbagai mod Gambar di atas adalah bengkel kecerdasan buatan pertama yang diadakan di Kolej Dartmouth di Amerika Syarikat pada tahun 1956. Persidangan ini juga dianggap telah memulakan pembangunan kecerdasan buatan perintis logik simbolik (kecuali ahli neurobiologi Peter Milner di tengah-tengah barisan hadapan). Walau bagaimanapun, teori logik simbolik ini tidak dapat direalisasikan untuk masa yang lama, malah memulakan musim sejuk AI pertama pada 1980-an dan 1990-an. Sehingga pelaksanaan model bahasa besar baru-baru ini, kami mendapati bahawa rangkaian saraf benar-benar membawa pemikiran logik ini. Kerja ahli neurobiologi Peter Milner memberi inspirasi kepada pembangunan rangkaian saraf tiruan yang seterusnya, dan atas sebab inilah dia dijemput untuk mengambil bahagian. dalam projek ini.
 Aplikasi algoritma dalam pembinaan 58 platform potret
May 09, 2024 am 09:01 AM
Aplikasi algoritma dalam pembinaan 58 platform potret
May 09, 2024 am 09:01 AM
1. Latar Belakang Pembinaan 58 Portrait Platform Pertama sekali, saya ingin berkongsi dengan anda latar belakang pembinaan 58 Portrait Platform. 1. Pemikiran tradisional platform pemprofilan tradisional tidak lagi mencukupi Membina platform pemprofilan pengguna bergantung pada keupayaan pemodelan gudang data untuk menyepadukan data daripada pelbagai barisan perniagaan untuk membina potret pengguna yang tepat untuk memahami tingkah laku, minat pengguna dan keperluan, dan menyediakan keupayaan sampingan, akhirnya, ia juga perlu mempunyai keupayaan platform data untuk menyimpan, bertanya dan berkongsi data profil pengguna dan menyediakan perkhidmatan profil dengan cekap. Perbezaan utama antara platform pemprofilan perniagaan binaan sendiri dan platform pemprofilan pejabat pertengahan ialah platform pemprofilan binaan sendiri menyediakan satu barisan perniagaan dan boleh disesuaikan atas permintaan platform pertengahan pejabat berkhidmat berbilang barisan perniagaan, mempunyai kompleks pemodelan, dan menyediakan lebih banyak keupayaan umum. 2.58 Potret pengguna latar belakang pembinaan potret di platform tengah 58
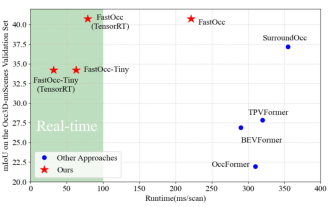 Tambah SOTA dalam masa nyata dan meroket! FastOcc: Inferens yang lebih pantas dan algoritma Occ mesra penggunaan sudah tersedia!
Mar 14, 2024 pm 11:50 PM
Tambah SOTA dalam masa nyata dan meroket! FastOcc: Inferens yang lebih pantas dan algoritma Occ mesra penggunaan sudah tersedia!
Mar 14, 2024 pm 11:50 PM
Ditulis di atas & Pemahaman peribadi penulis ialah dalam sistem pemanduan autonomi, tugas persepsi adalah komponen penting dalam keseluruhan sistem pemanduan autonomi. Matlamat utama tugas persepsi adalah untuk membolehkan kenderaan autonomi memahami dan melihat elemen persekitaran sekeliling, seperti kenderaan yang memandu di jalan raya, pejalan kaki di tepi jalan, halangan yang dihadapi semasa memandu, tanda lalu lintas di jalan raya, dan sebagainya, dengan itu membantu hiliran. modul Membuat keputusan dan tindakan yang betul dan munasabah. Kenderaan dengan keupayaan pemanduan autonomi biasanya dilengkapi dengan pelbagai jenis penderia pengumpulan maklumat, seperti penderia kamera pandangan sekeliling, penderia lidar, penderia radar gelombang milimeter, dsb., untuk memastikan kenderaan autonomi itu dapat melihat dan memahami persekitaran sekeliling dengan tepat. elemen , membolehkan kenderaan autonomi membuat keputusan yang betul semasa pemanduan autonomi. kepala




