nombor heptagon-C++-php.cn

nombor heptagon

王林

Lepaskan： 2023-09-24 10:33:08

ke hadapan

1254 orang telah melayarinya

Nombor heptagonal ialah nombor yang boleh diwakili sebagai heptagon Nombor heptagonal boleh diwakili sebagai gabungan lapisan berturut-turut bagi heptagon(poligon 7 sisi diterangkan dengan angka di bawah.

Nombor heptagonal pertama ialah 1. Oleh itu, ia boleh diwakili oleh titik kecil.

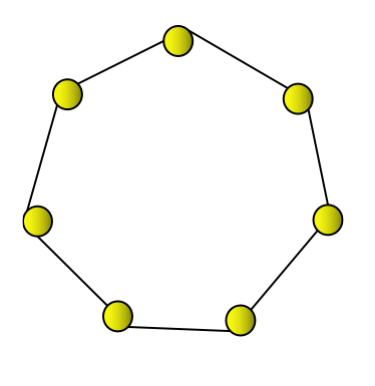
Nombor heptagon kedua ialah 7, yang boleh diwakili oleh heptagon.

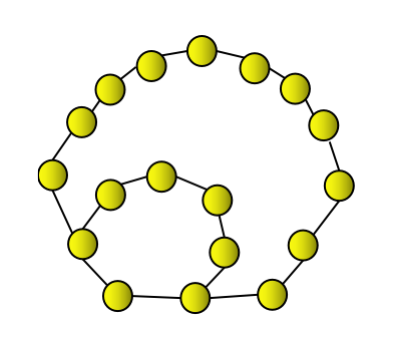
Nombor heptagon ketiga ialah 18, yang boleh diwakili oleh heptagon dan digabungkan dengan lapisan heptagon berterusan.

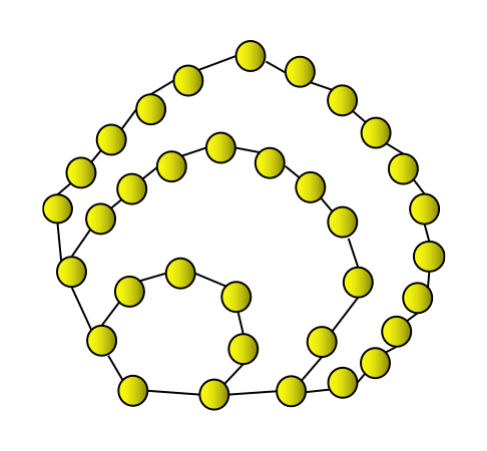
Nombor heptagonal keempat ialah 34. Ia boleh diwakili dalam cara yang ditunjukkan di atas sebagai heptagon ditambah dua lapisan berturut-turut heptagon, memberikan 34.

Konsep serupa akan digunakan untuk nombor heptagonal selanjutnya. Mengikut logik yang sama, beberapa nombor heptagonal pertama ialah 1, 7, 18, 34, 55, 81, 112, 148, 189, 235, 286, 342, 403…

Dalam masalah ini, tugas kita adalah untuk memberikan sebarang nombor positif N sebagai input dan mencetak nombor heptagon Nth sebagai output.

Sebagai contoh,

INPUT : N=6

Output : 81

INPUT : N=9

Output: 189

Sekarang mari kita lihat algoritma yang akan kita gunakan untuk menyelesaikan masalah ini.

Algoritma

Untuk menyelesaikan masalah ini, kita perlu melihat corak diikuti dengan mengira nombor heptagonal ke-n. Nombor heptagonal ke-n boleh dinyatakan sebagai −

$$Heptagonal_{n}:=:frac{n}{2}(5n:-:3)$$

Jika kita melihat ungkapan ini dengan teliti, setiap nombor heptagonal mempunyai bentuk berikut

$frac{n}{2}(5n:-:3)$, dengan n mewakili bilangan nombor heptagonal.

Mari kita memahaminya dengan lebih baik dengan contoh.

Untuk n=1, $frac{1}{2}(5:times:1:-:3)$= 1, iaitu nombor heptagonal pertama.

Untuk n=2, $frac{2}{2}(5:times:2:-:3)$= 7, iaitu nombor heptagonal kedua.

Apabila n=3, $frac{3}{2}(5:times:3:-:3)$= 18, iaitu nombor heptagonal ketiga.

Sekarang, mari kita semak kes n=8. Hasil yang diperolehi oleh $frac{8}{2}(5:times:8:-:3)$ ialah 148, yang sebenarnya ialah nombor heptagonal kelapan dalam jujukan nombor heptagonal.

Memandangkan kita boleh mendapatkan sebarang nombor heptagonal ke-n menggunakan ungkapan di atas, jadi dalam kaedah kita, kita akan menggunakan ungkapan ini untuk mengira nombor heptagonal ke-n, di mana n boleh menjadi sebarang nombor positif.

Kaedah

Kami akan menerangkan dalam langkah berikut:

Ambil sebarang nombor positif N sebagai input dan hitung nilai heptagon N yang sepadan.
Mulakan fungsi untuk mengira nombor heptagon ke-N.
Gunakan ungkapan yang disebut dalam bahagian algoritma, iaitu $frac{N}{2}(5N:-:3)$, untuk mengira nombor heptagon N dan menyimpannya dalam pembolehubah arbitrari.
Mengembalikan pembolehubah tersimpan kami yang akan menjadi nilai nombor heptagonal N yang sepadan dengan sebarang nilai positif N.

Nota − Kami akan menggunakan jenis data titik terapung dan bukannya jenis data integer untuk mengelakkan sebarang ralat disebabkan oleh nilai perpuluhan semasa mengira nombor heptagonal N menggunakan formula di atas.

Terjemahan bahasa Cina bagi

Contoh

ialah:

Contoh

Laksanakan kaedah ini dalam C++ −

#include <bits/stdc++.h>
#include <iostream>
using namespace std;

//function to calculate nth heptagonal number using formula n/2(5n-3)
float heptagonal(float N){
   float ans= (N/2)*((5*N) - 3); //to store nth heptagonal number
   return ans;
}
int main(){
   float N=5; //input
   float a=heptagonal(N); //store the answer in a variable
   N=13;
   float b=heptagonal(N);
   cout<<a<<endl<<b<<endl; //print the answer
   return 0;
}

Salin selepas log masuk