
Taburan multimodal satu dimensi boleh dibahagikan kepada berbilang taburan menggunakan Model Campuran Gaussian
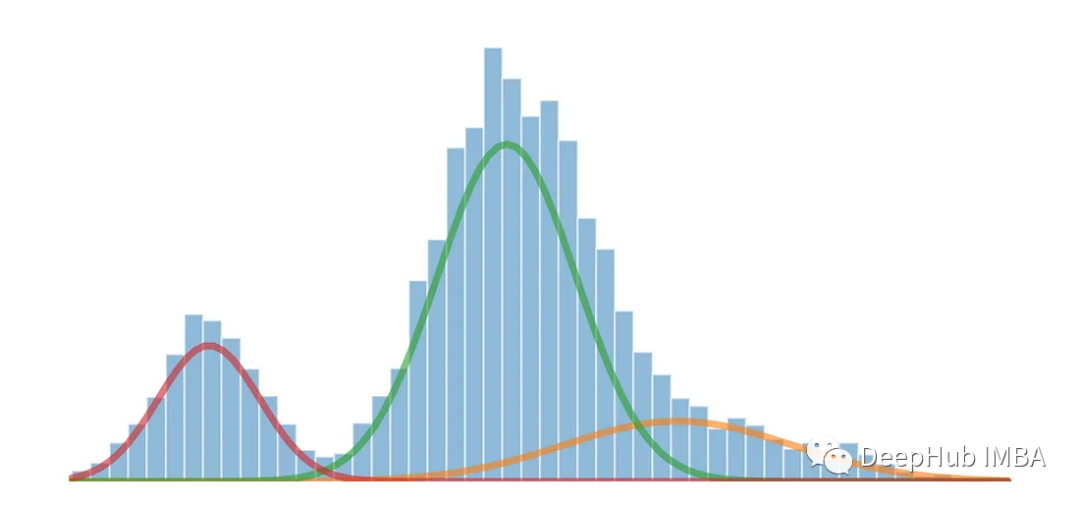
Model Campuran Gaussian (GMM) ialah kaedah yang biasa digunakan dalam bidang statistik dan pembelajaran mesin untuk model kebarangkalian dan model menganalisis taburan data yang kompleks. GMM ialah model generatif yang menganggap bahawa data yang diperhatikan terdiri daripada berbilang taburan Gaussian, setiap taburan Gaussian dipanggil komponen, dan komponen ini mengawal sumbangannya dalam data melalui pemberat.
Apabila set data menunjukkan berbilang puncak atau mod yang berbeza, ini biasanya bermakna terdapat berbilang kelompok atau kepekatan titik data yang menonjol dalam set data. Setiap mod mewakili kelompok atau kepekatan titik data yang menonjol dalam pengedaran dan boleh dianggap sebagai kawasan berketumpatan tinggi di mana nilai data lebih berkemungkinan berlaku
Kami akan menggunakan tatasusunan satu dimensi yang dijana oleh numpy .
import numpy as np dist_1 = np.random.normal(10, 3, 1000) dist_2 = np.random.normal(30, 5, 4000) dist_3 = np.random.normal(45, 6, 500) multimodal_dist = np.concatenate((dist_1, dist_2, dist_3), axis=0)
Mari kita bayangkan pengedaran data satu dimensi. . Model campuran Gaussian ialah model probabilistik tanpa pengawasan yang boleh digunakan untuk pengelompokan data. Ia menggunakan algoritma pemaksimum jangkaan untuk menganggarkan kawasan ketumpatan
import matplotlib.pyplot as plt import seaborn as sns sns.set_style('whitegrid') plt.hist(multimodal_dist, bins=50, alpha=0.5) plt.show()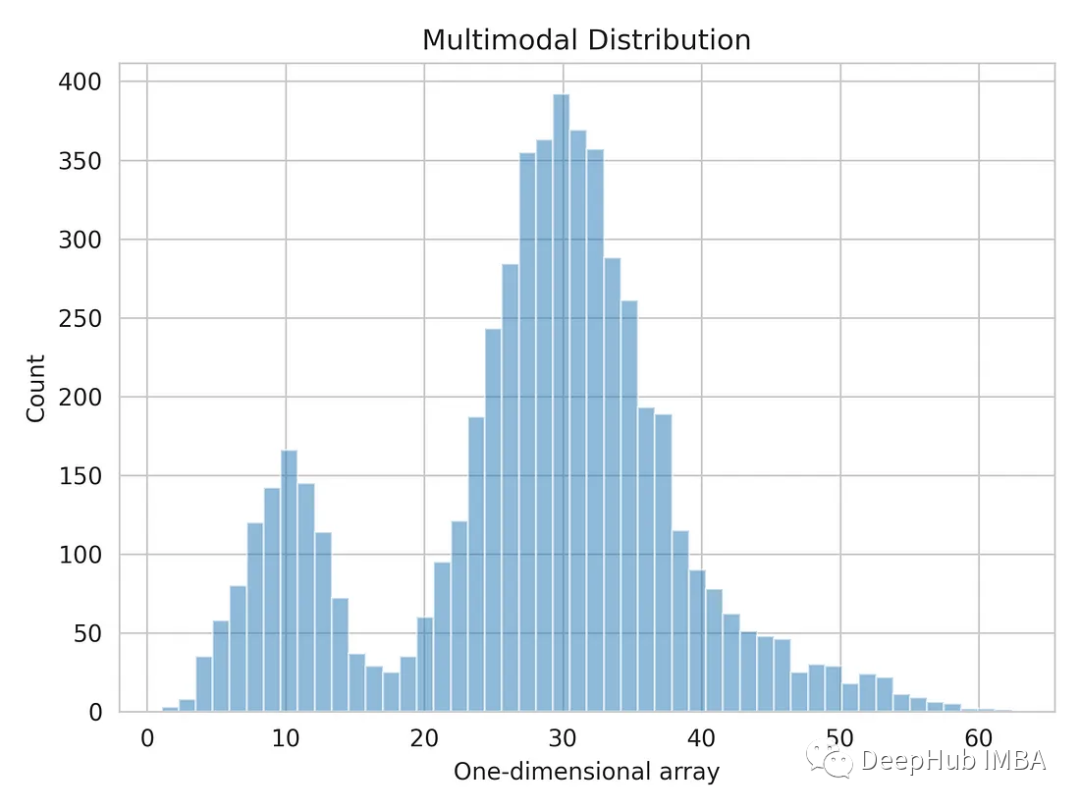 Kami sudah mempunyai min dan sisihan piawai untuk memodelkan taburan asal. Anda boleh melihat bahawa walaupun min dan sisihan piawai mungkin tidak betul, ia memberikan anggaran yang hampir.
Kami sudah mempunyai min dan sisihan piawai untuk memodelkan taburan asal. Anda boleh melihat bahawa walaupun min dan sisihan piawai mungkin tidak betul, ia memberikan anggaran yang hampir.
from sklearn.mixture import GaussianMixture gmm = GaussianMixture(n_compnotallow=3) gmm.fit(multimodal_dist.reshape(-1, 1)) means = gmm.means_ # Conver covariance into Standard Deviation standard_deviations = gmm.covariances_**0.5 # Useful when plotting the distributions later weights = gmm.weights_ print(f"Means: {means}, Standard Deviations: {standard_deviations}") #Means: [29.4, 10.0, 38.9], Standard Deviations: [4.6, 3.1, 7.9]Ringkasan
Model campuran Gaussian ialah alat berkuasa yang boleh digunakan untuk memodelkan dan menganalisis pengagihan data yang kompleks, dan juga merupakan salah satu asas kepada banyak algoritma pembelajaran mesin. Ia mempunyai pelbagai aplikasi dan boleh menyelesaikan pelbagai masalah pemodelan dan analisis data
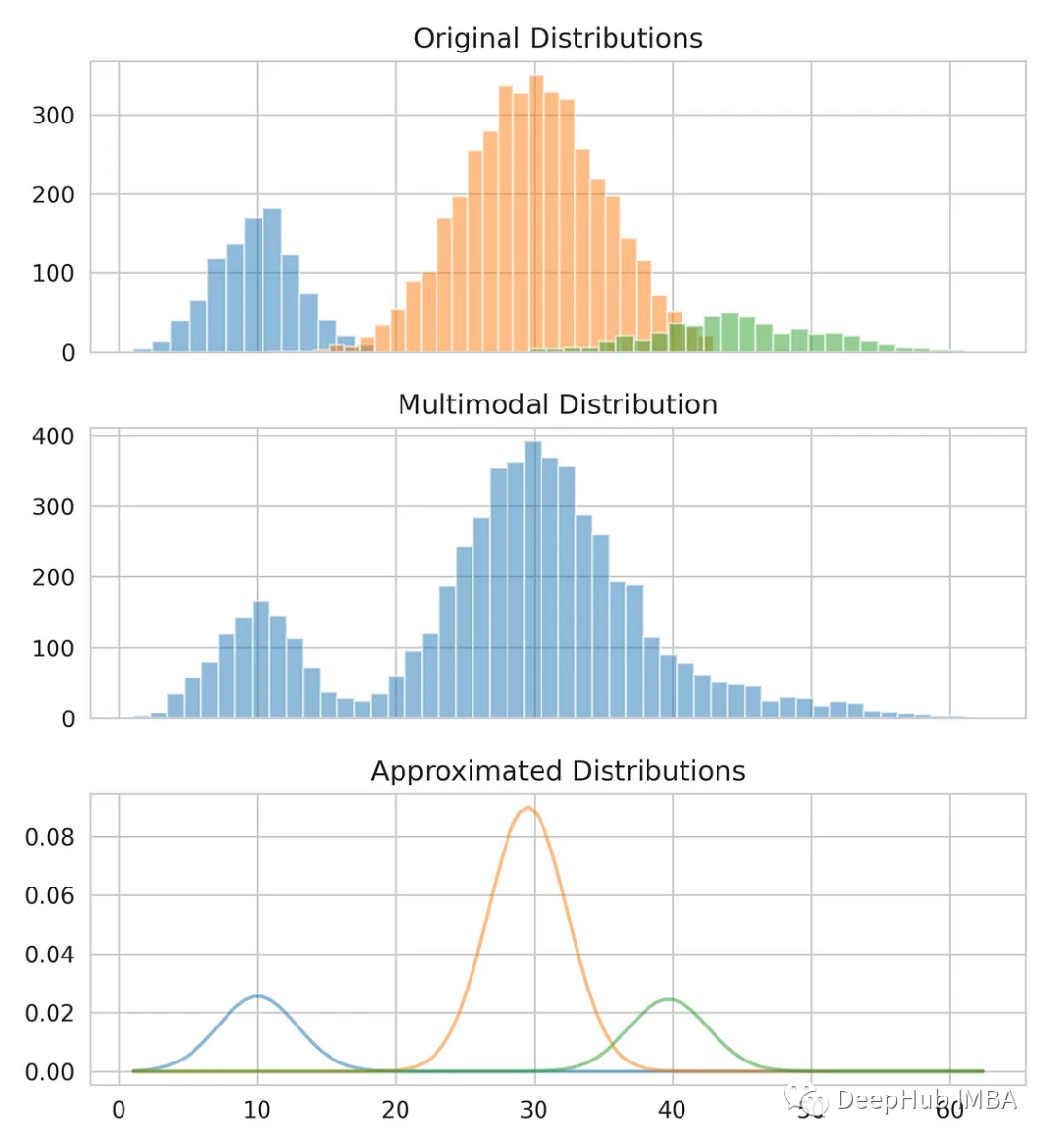 Kaedah ini boleh digunakan sebagai teknik kejuruteraan ciri untuk menganggarkan selang keyakinan subagihan dalam pembolehubah input
Kaedah ini boleh digunakan sebagai teknik kejuruteraan ciri untuk menganggarkan selang keyakinan subagihan dalam pembolehubah input
Atas ialah kandungan terperinci Mengurai taburan pelbagai mod menggunakan model campuran Gaussian. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!




