 Peranti teknologi
Peranti teknologi
 AI
AI
 Lebih serba boleh dan berkesan, WSAM pengoptimum yang dibangunkan sendiri oleh Ant telah dipilih ke dalam KDD Oral
Lebih serba boleh dan berkesan, WSAM pengoptimum yang dibangunkan sendiri oleh Ant telah dipilih ke dalam KDD Oral
Lebih serba boleh dan berkesan, WSAM pengoptimum yang dibangunkan sendiri oleh Ant telah dipilih ke dalam KDD Oral
Keupayaan generalisasi rangkaian saraf dalam (DNN) berkait rapat dengan kerataan titik ekstrem, jadi algoritma Sharpness-Aware Minimization (SAM) muncul untuk mencari titik ekstrem yang lebih rata untuk meningkatkan keupayaan generalisasi. Kertas kerja ini mengkaji semula fungsi kehilangan SAM dan mencadangkan kaedah yang lebih umum dan berkesan, WSAM, untuk meningkatkan kerataan latihan mata ekstrem dengan menggunakan kerataan sebagai istilah regularisasi. Percubaan pada pelbagai set data awam menunjukkan bahawa WSAM mencapai prestasi generalisasi yang lebih baik dalam kebanyakan kes berbanding dengan pengoptimum asal, SAM dan variannya. WSAM juga telah diterima pakai secara meluas dalam pembayaran digital dalaman Ant, kewangan digital dan senario lain dan telah mencapai hasil yang luar biasa. Kertas kerja ini diterima sebagai Kertas Lisan oleh KDD '23.

- Alamat kertas: https://arxiv.org/pdf/2305.15817.pdf
- /intelli gent - machine-learning/dlrover/tree/master/torch/torch/optimizers
Penyelidikan terkini menunjukkan bahawa keupayaan generalisasi berkait rapat dengan kerataan titik ekstrem. Dalam erti kata lain, kehadiran titik ekstrem rata dalam "landskap" fungsi kehilangan membolehkan ralat generalisasi yang lebih kecil. Sharpness-Aware Minimization (SAM) [1] ialah teknik untuk mencari titik ekstrem yang lebih rata dan dianggap sebagai salah satu arah teknikal yang paling menjanjikan pada masa ini. Teknologi SAM digunakan secara meluas dalam banyak bidang seperti penglihatan komputer, pemprosesan bahasa semula jadi, dan pembelajaran dua lapisan, dan dengan ketara mengatasi kaedah terkini yang terkini dalam bidang ini
Untuk meneroka minima yang lebih rata, SAM mentakrifkan fungsi kehilangan Kerataan
L pada w adalah seperti berikut:
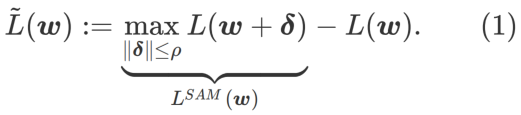
ialah anggaran nilai eigeniks maksimum bagi maksima ekstrem Hessian yang Artikel ini memikirkan semula pembinaan SAM ialah teknik untuk menyelesaikan masalah pengoptimuman minimax Pertama, SAM menggunakan pengembangan Taylor tertib pertama di sekitar w untuk menganggarkan masalah pemaksimuman lapisan dalam, iaitu, , Kedua, SAM kemas kini Pengiraan kedua adalah untuk mempercepatkan pengiraan. Pengoptimum berasaskan kecerunan lain (dipanggil pengoptimum asas) boleh dimasukkan ke dalam rangka kerja umum SAM, lihat Algoritma 1 untuk butiran. Dengan menukar Antaranya dan # yang berbeza 🎜 🎜# Rajah 1 menunjukkan proses kemas kini WSAM di bawah nilai 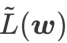 memang rata (curam) Pengukuran berkesan. Walau bagaimanapun, hanya boleh digunakan untuk mencari kawasan yang lebih rata dan bukannya titik minimum, yang mungkin menyebabkan fungsi kehilangan menumpu ke titik di mana nilai kerugian masih besar (walaupun kawasan sekitar rata). Oleh itu, SAM menggunakan
memang rata (curam) Pengukuran berkesan. Walau bagaimanapun, hanya boleh digunakan untuk mencari kawasan yang lebih rata dan bukannya titik minimum, yang mungkin menyebabkan fungsi kehilangan menumpu ke titik di mana nilai kerugian masih besar (walaupun kawasan sekitar rata). Oleh itu, SAM menggunakan 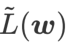
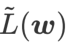 , iaitu
, iaitu 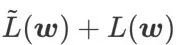 sebagai fungsi kerugian. Ia boleh dilihat sebagai kompromi antara mencari permukaan yang lebih rata dan nilai kerugian yang lebih kecil antara
sebagai fungsi kerugian. Ia boleh dilihat sebagai kompromi antara mencari permukaan yang lebih rata dan nilai kerugian yang lebih kecil antara 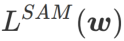 dan
dan 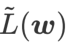 , di mana kedua-duanya diberi berat yang sama.
, di mana kedua-duanya diberi berat yang sama. 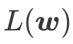
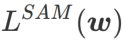 dan menganggap
dan menganggap 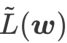 sebagai istilah regularisasi. Kami membangunkan algoritma yang lebih umum dan berkesan yang dipanggil WSAM (Pengurangan Ketajaman Berwajaran) menambah istilah kerataan berwajaran
sebagai istilah regularisasi. Kami membangunkan algoritma yang lebih umum dan berkesan yang dipanggil WSAM (Pengurangan Ketajaman Berwajaran) menambah istilah kerataan berwajaran 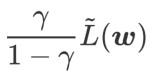 sebagai istilah penyelarasan, di mana hiperparameter
sebagai istilah penyelarasan, di mana hiperparameter 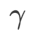 mengawal kerataan. Dalam bab pengenalan kaedah, kami menunjukkan cara menggunakan
mengawal kerataan. Dalam bab pengenalan kaedah, kami menunjukkan cara menggunakan 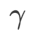 untuk membimbing fungsi kehilangan untuk mencari titik ekstrem yang lebih rata atau lebih kecil. Sumbangan utama kami boleh diringkaskan seperti berikut.
untuk membimbing fungsi kehilangan untuk mencari titik ekstrem yang lebih rata atau lebih kecil. Sumbangan utama kami boleh diringkaskan seperti berikut.
Pengetahuan awal
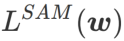 yang ditakrifkan oleh formula (1).
yang ditakrifkan oleh formula (1). 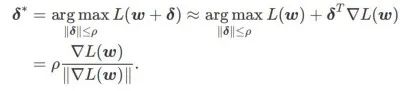
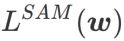 ximate w dengan mengambil kira-kira gradient iaitu
ximate w dengan mengambil kira-kira gradient iaitu 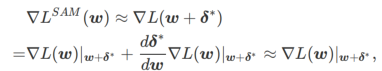
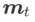 dan
dan 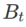 dalam Algoritma 1, kita boleh mendapatkan pengoptimum asas yang berbeza, seperti SGD, SGDM dan Adam, lihat Tab 1. Ambil perhatian bahawa Algoritma 1 kembali kepada SAM asal daripada kertas SAM [1] apabila pengoptimum asas ialah SGD. . Daripada formula (1), kami ada
dalam Algoritma 1, kita boleh mendapatkan pengoptimum asas yang berbeza, seperti SGD, SGDM dan Adam, lihat Tab 1. Ambil perhatian bahawa Algoritma 1 kembali kepada SAM asal daripada kertas SAM [1] apabila pengoptimum asas ialah SGD. . Daripada formula (1), kami ada 
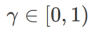 . Apabila
. Apabila 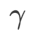 =0 ,
=0 , 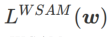 merosot menjadi kerugian biasa; Apabila 2, bersamaan dengan
merosot menjadi kerugian biasa; Apabila 2, bersamaan dengan 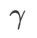 ; apabila
; apabila 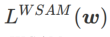
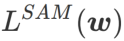 >1/2, memberi perhatian lebih kepada kerataan, jadi lebih mudah untuk dibandingkan dengan SAM Cari mata dengan kelengkungan yang lebih kecil daripada nilai kerugian yang lebih kecil dan sebaliknya.
>1/2, memberi perhatian lebih kepada kerataan, jadi lebih mudah untuk dibandingkan dengan SAM Cari mata dengan kelengkungan yang lebih kecil daripada nilai kerugian yang lebih kecil dan sebaliknya. 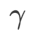
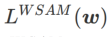 Rangka kerja biasa untuk WSAM yang mengandungi pengoptimum asas yang berbeza boleh dibuat dengan memilih
Rangka kerja biasa untuk WSAM yang mengandungi pengoptimum asas yang berbeza boleh dibuat dengan memilih 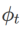 untuk dilaksanakan, lihat Algoritma 2. Contohnya, apabila
untuk dilaksanakan, lihat Algoritma 2. Contohnya, apabila 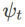 dan
dan  , kita mendapat WSAM yang pengoptimum asasnya ialah SGD, lihat Algoritma 3. Di sini, kami menggunakan teknik "penyahgandingan berat", iaitu istilah kerataan tidak disepadukan dengan pengoptimum asas untuk mengira kecerunan dan mengemas kini pemberat, tetapi dikira secara bebas (baris terakhir Algoritma 2 baris 7 item). Dengan cara ini, kesan regularisasi hanya mencerminkan kerataan langkah semasa tanpa maklumat tambahan. Sebagai perbandingan, Algoritma 4 memberikan WSAM tanpa "penyahgandingan berat" (dipanggil Coupled-WSAM). Contohnya, jika pengoptimum asas ialah SGDM, istilah regularisasi Coupled-WSAM ialah purata bergerak eksponen bagi kerataan. Seperti yang ditunjukkan dalam bahagian percubaan, "penyahgandingan berat" boleh meningkatkan prestasi generalisasi dalam kebanyakan kes.
, kita mendapat WSAM yang pengoptimum asasnya ialah SGD, lihat Algoritma 3. Di sini, kami menggunakan teknik "penyahgandingan berat", iaitu istilah kerataan tidak disepadukan dengan pengoptimum asas untuk mengira kecerunan dan mengemas kini pemberat, tetapi dikira secara bebas (baris terakhir Algoritma 2 baris 7 item). Dengan cara ini, kesan regularisasi hanya mencerminkan kerataan langkah semasa tanpa maklumat tambahan. Sebagai perbandingan, Algoritma 4 memberikan WSAM tanpa "penyahgandingan berat" (dipanggil Coupled-WSAM). Contohnya, jika pengoptimum asas ialah SGDM, istilah regularisasi Coupled-WSAM ialah purata bergerak eksponen bagi kerataan. Seperti yang ditunjukkan dalam bahagian percubaan, "penyahgandingan berat" boleh meningkatkan prestasi generalisasi dalam kebanyakan kes. 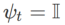
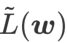

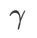 yang berbeza. Apabila
yang berbeza. Apabila 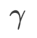 ,
, 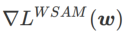 berada di antara
berada di antara 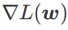 dan #🎜 🎜🎜# dan secara beransur-ansur menyimpang daripada
dan #🎜 🎜🎜# dan secara beransur-ansur menyimpang daripada 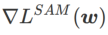
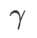 apabila meningkat.
apabila meningkat. 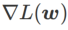

#🎜🎜🎜 Untuk saya #🎜🎜 Untuk lebih baik saya##🎜 kesan dan kelebihan γ dalam WSAM, kami menyediakan contoh dua dimensi yang mudah. Seperti yang ditunjukkan dalam Rajah 2, fungsi kerugian mempunyai titik ekstrem yang agak tidak sekata di sudut kiri bawah (kedudukan: (-16.8, 12.8), nilai kerugian: 0.28), dan titik ekstrem rata di sudut kanan atas (kedudukan: (19.8, 29.9), nilai kerugian: 0.36). Fungsi kehilangan ditakrifkan sebagai:
, di mana 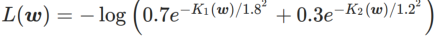 ialah perbezaan KL antara model Gaussian univariate dan dua taburan normal, iaitu
ialah perbezaan KL antara model Gaussian univariate dan dua taburan normal, iaitu 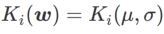 , antaranya
, antaranya 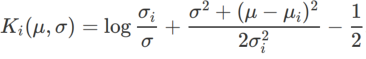 dan
dan 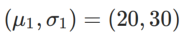 .
. 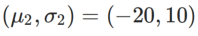 Kami menggunakan SGDM dengan momentum 0.9 sebagai pengoptimum asas dan menetapkan
Kami menggunakan SGDM dengan momentum 0.9 sebagai pengoptimum asas dan menetapkan
=2 untuk SAM dan WSAM. Bermula dari titik awal (-6, 10), fungsi kehilangan dioptimumkan dalam 150 langkah menggunakan kadar pembelajaran 5. SAM menumpu ke titik ekstrem dengan nilai kerugian yang lebih rendah tetapi lebih tidak sekata, dan WSAM dengan 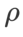 =0.6 adalah serupa. Walau bagaimanapun,
=0.6 adalah serupa. Walau bagaimanapun, 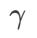 =0.95 menyebabkan fungsi kehilangan menumpu ke titik ekstrem rata, menunjukkan bahawa regularisasi kerataan yang lebih kuat memainkan peranan.
=0.95 menyebabkan fungsi kehilangan menumpu ke titik ekstrem rata, menunjukkan bahawa regularisasi kerataan yang lebih kuat memainkan peranan. 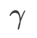
Eksperimen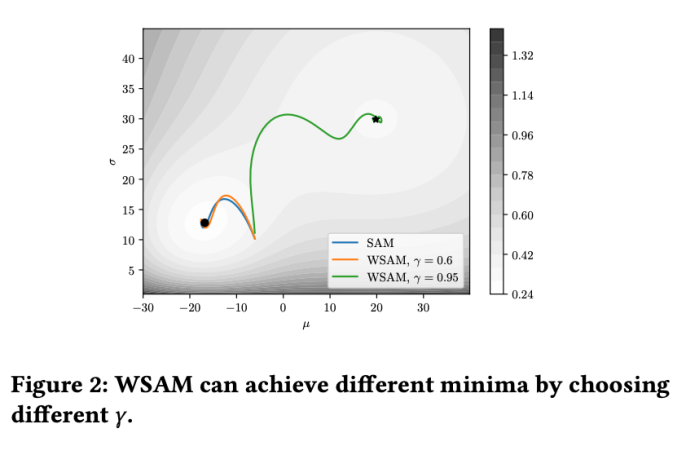
#🎜🎜 sedang mengusahakan pelbagai tugasan Eksperimen telah dijalankan untuk mengesahkan keberkesanan WSAM.
Klasifikasi Imej
Kami mula-mula mempelajari latihan WSAM dari awal pada set data Cifar10 dan Cifar100 Model yang kami pilih termasuk ResNet18 dan WideResNet-28-10. Kami melatih model pada Cifar10 dan Cifar100 menggunakan saiz kelompok yang dipratentukan masing-masing 128, 256 untuk ResNet18 dan WideResNet-28-10. Pengoptimum asas yang digunakan di sini ialah SGDM dengan momentum 0.9. Menurut tetapan SAM [1], setiap pengoptimum asas menjalankan dua kali bilangan zaman sebagai pengoptimum kelas SAM. Kami melatih kedua-dua model untuk 400 zaman (200 zaman untuk pengoptimum kelas SAM) dan menggunakan penjadual kosinus untuk mereputkan kadar pembelajaran. Di sini kami tidak menggunakan kaedah penambahan data lanjutan lain seperti potongan dan AutoAugment.
Untuk kedua-dua model, kami menggunakan carian grid bersama untuk menentukan kadar pembelajaran dan pekali pereputan berat bagi pengoptimum asas dan memastikannya tetap untuk eksperimen pengoptimum kelas SAM berikut. Julat carian kadar pembelajaran dan pekali pereputan berat ialah {0.05, 0.1} dan {1e-4, 5e-4, 1e-3} masing-masing. Memandangkan semua pengoptimum kelas SAM mempunyai satu hiperparameter 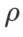 (saiz kejiranan), kami seterusnya mencari
(saiz kejiranan), kami seterusnya mencari 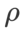 terbaik pada pengoptimum SAM dan menggunakan nilai yang sama untuk pengoptimum kelas SAM yang lain. Julat carian
terbaik pada pengoptimum SAM dan menggunakan nilai yang sama untuk pengoptimum kelas SAM yang lain. Julat carian 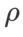 ialah {0.01, 0.02, 0.05, 0.1, 0.2, 0.5}. Akhir sekali, kami mencari hiperparameter unik pengoptimum kelas SAM yang lain, dan julat carian datang daripada julat yang disyorkan artikel asal masing-masing. Untuk GSAM [2], kami mencari dalam julat {0.01, 0.02, 0.03, 0.1, 0.2, 0.3}. Untuk ESAM [3], kami mencari
ialah {0.01, 0.02, 0.05, 0.1, 0.2, 0.5}. Akhir sekali, kami mencari hiperparameter unik pengoptimum kelas SAM yang lain, dan julat carian datang daripada julat yang disyorkan artikel asal masing-masing. Untuk GSAM [2], kami mencari dalam julat {0.01, 0.02, 0.03, 0.1, 0.2, 0.3}. Untuk ESAM [3], kami mencari  dalam julat {0.4, 0.5, 0.6},
dalam julat {0.4, 0.5, 0.6}, 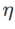 dalam julat {0.4, 0.5, 0.6} dan
dalam julat {0.4, 0.5, 0.6} dan 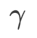 dalam julat {0.4, 0. , 0.6}. . Untuk WSAM, kami mencari
dalam julat {0.4, 0. , 0.6}. . Untuk WSAM, kami mencari 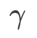 dalam julat {0.5, 0.6, 0.7, 0.8, 0.82, 0.84, 0.86, 0.88, 0.9, 0.92, 0.94, 0.96}. Kami mengulangi eksperimen 5 kali menggunakan benih rawak yang berbeza dan mengira ralat min dan sisihan piawai. Kami menjalankan percubaan pada GPU NVIDIA A100 kad tunggal. Hiperparameter pengoptimum untuk setiap model diringkaskan dalam Tab 3.
dalam julat {0.5, 0.6, 0.7, 0.8, 0.82, 0.84, 0.86, 0.88, 0.9, 0.92, 0.94, 0.96}. Kami mengulangi eksperimen 5 kali menggunakan benih rawak yang berbeza dan mengira ralat min dan sisihan piawai. Kami menjalankan percubaan pada GPU NVIDIA A100 kad tunggal. Hiperparameter pengoptimum untuk setiap model diringkaskan dalam Tab 3.
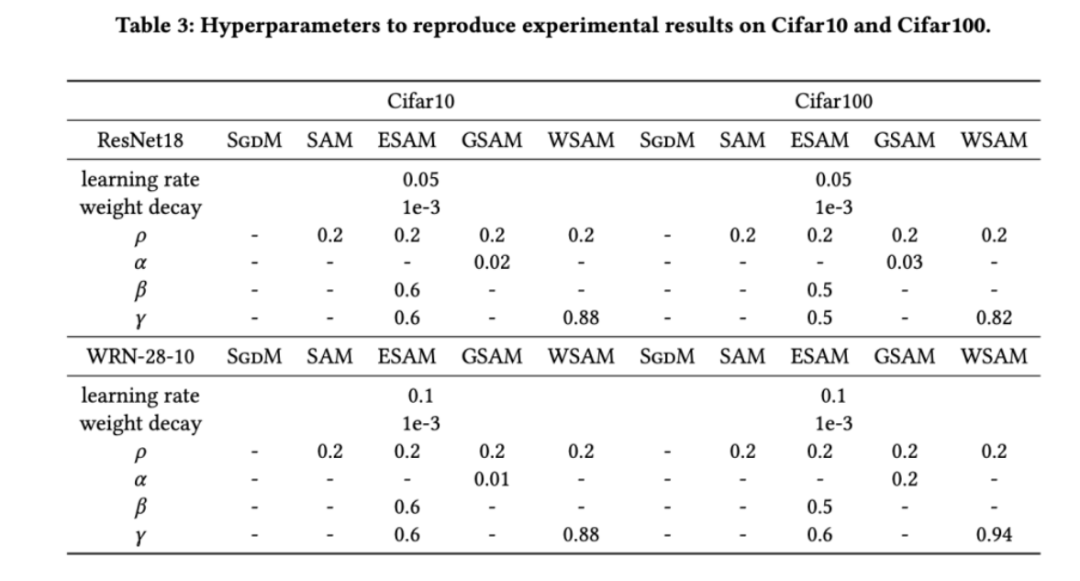
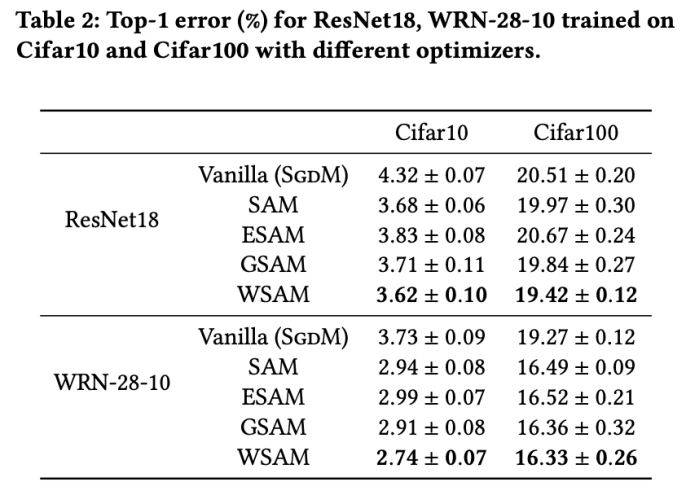
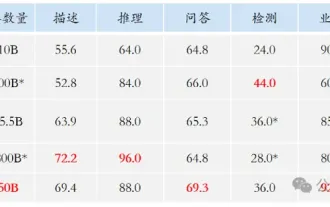
Tab 2 memberikan kadar ralat 1 teratas ResNet18, WRN-28-10 pada set ujian pada Cifar10 dan Cifar100 di bawah pengoptimum yang berbeza. Berbanding dengan pengoptimum asas, pengoptimum kelas SAM dengan ketara meningkatkan prestasi Pada masa yang sama, WSAM jauh lebih baik daripada pengoptimum kelas SAM yang lain.
Latihan tambahan pada ImageNet
Kami selanjutnya menjalankan eksperimen pada dataset ImageNet menggunakan struktur rangkaian Transformers Imej Cekap Data. Kami menyambung semula pusat pemeriksaan pangkalan DeiT yang telah terlatih dan kemudian meneruskan latihan selama tiga zaman. Model ini dilatih menggunakan saiz kelompok 256, pengoptimum asas ialah SGDM dengan momentum 0.9, pekali pengecilan berat ialah 1e-4, dan kadar pembelajaran ialah 1e-5. Kami mengulangi larian 5 kali pada GPU NVIDIA A100 empat kad dan mengira ralat purata dan sisihan piawai
Kami mencari 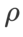 terbaik SAM dalam {0.05, 0.1, 0.5, 1.0,⋯} ,
terbaik SAM dalam {0.05, 0.1, 0.5, 1.0,⋯} , 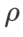 terbaik .
terbaik .  =5.5 yang optimum digunakan secara langsung dalam pengoptimum kelas SAM yang lain. Selepas itu, kami mencari
=5.5 yang optimum digunakan secara langsung dalam pengoptimum kelas SAM yang lain. Selepas itu, kami mencari 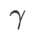 GSAM terbaik dalam {0.01, 0.02, 0.03, 0.1, 0.2, 0.3} dan
GSAM terbaik dalam {0.01, 0.02, 0.03, 0.1, 0.2, 0.3} dan
terbaik WSAM antara 0.80 dan 0.98 dengan saiz langkah 0.02
Kadar ralat top-1 awal model ialah 18.2%, dan selepas tiga zaman tambahan, kadar ralat ditunjukkan dalam Tab 4. Kami tidak menemui perbezaan ketara antara tiga pengoptimum seperti SAM, tetapi semuanya mengatasi pengoptimuman asas, menunjukkan bahawa mereka boleh menemui titik ekstrem yang lebih rata dan mempunyai keupayaan generalisasi yang lebih baik. 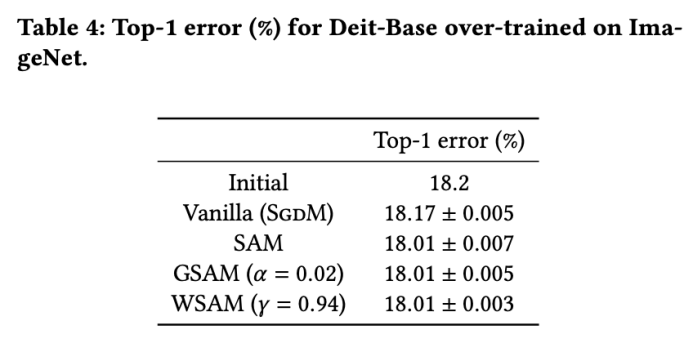
Keteguhan untuk melabel bunyi
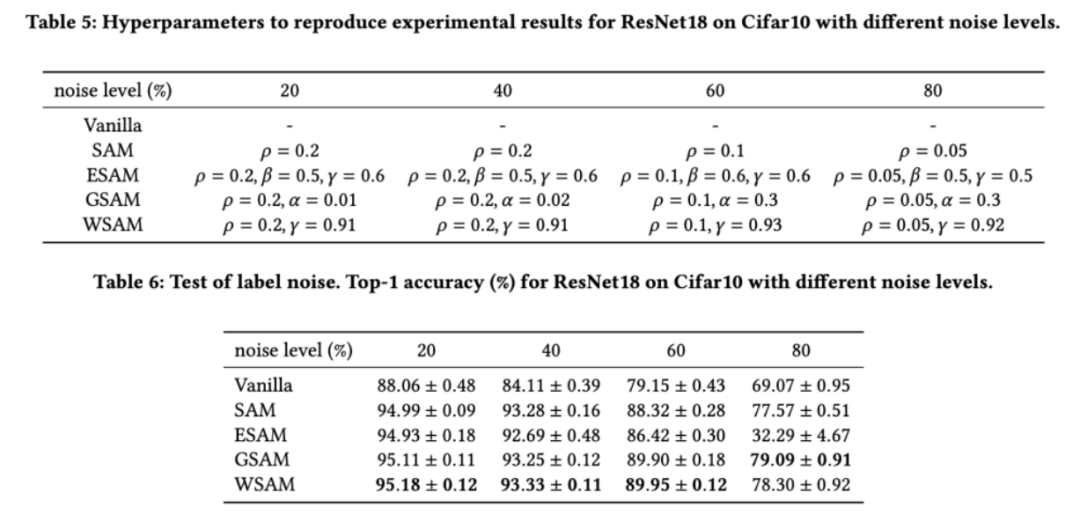
Seperti yang ditunjukkan dalam kajian terdahulu [1, 4, 5], pengoptimum kelas SAM dilatih Set menunjukkan keteguhan yang baik dengan kehadiran bunyi label. Di sini, kami membandingkan kekukuhan WSAM dengan SAM, ESAM dan GSAM. Kami melatih ResNet18 pada set data Cifar10 untuk 200 zaman dan menyuntik hingar label simetri dengan tahap hingar sebanyak 20%, 40%, 60% dan 80%. Kami menggunakan SGDM dengan momentum 0.9 sebagai pengoptimum asas, saiz kelompok 128, kadar pembelajaran 0.05, pekali pereputan berat 1e-3 dan penjadual kosinus untuk mereput kadar pembelajaran. Untuk setiap tahap hingar label, kami melakukan carian grid pada SAM dalam julat {0.01, 0.02, 0.05, 0.1, 0.2, 0.5} untuk menentukan nilai 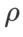 universal. Kami kemudian secara individu mencari hiperparameter khusus pengoptimum lain untuk mencari prestasi generalisasi optimum. Kami menyenaraikan hiperparameter yang diperlukan untuk menghasilkan semula keputusan kami dalam Tab 5. Kami membentangkan keputusan ujian kekukuhan dalam Tab 6. WSAM umumnya mempunyai kekukuhan yang lebih baik daripada SAM, ESAM dan GSAM.
universal. Kami kemudian secara individu mencari hiperparameter khusus pengoptimum lain untuk mencari prestasi generalisasi optimum. Kami menyenaraikan hiperparameter yang diperlukan untuk menghasilkan semula keputusan kami dalam Tab 5. Kami membentangkan keputusan ujian kekukuhan dalam Tab 6. WSAM umumnya mempunyai kekukuhan yang lebih baik daripada SAM, ESAM dan GSAM.
Meneroka kesan struktur geometri
#🎜🎜 Pengoptimum Kelas SAM boleh digabungkan dengan teknik seperti ASAM [4] dan Fisher SAM [5] untuk menyesuaikan bentuk kejiranan yang diterokai secara adaptif. Kami menjalankan eksperimen pada WRN-28-10 pada Cifar10 untuk membandingkan prestasi SAM dan WSAM apabila menggunakan kaedah maklumat adaptif dan Fisher, masing-masing, untuk memahami cara geometri kawasan penerokaan mempengaruhi prestasi generalisasi pengoptimum seperti SAM.
Kecuali parameter selain daripada 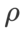 dan
dan 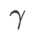 , kami menggunakan semula konfigurasi dalam pengelasan imej. Menurut kajian terdahulu [4, 5],
, kami menggunakan semula konfigurasi dalam pengelasan imej. Menurut kajian terdahulu [4, 5], 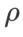 biasanya lebih besar untuk ASAM dan Fisher SAM. Kami mencari
biasanya lebih besar untuk ASAM dan Fisher SAM. Kami mencari 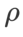 terbaik dalam {0.1, 0.5, 1.0,…, 6.0}, ASAM dan Fisher SAM untuk yang terbaik
terbaik dalam {0.1, 0.5, 1.0,…, 6.0}, ASAM dan Fisher SAM untuk yang terbaik 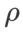 Kedua-duanya ialah 5.0. Selepas itu, kami mencari
Kedua-duanya ialah 5.0. Selepas itu, kami mencari 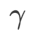 terbaik daripada WSAM antara 0.80 dan 0.94 dengan saiz langkah 0.02, dan kedua-dua kaedah adalah yang terbaik
terbaik daripada WSAM antara 0.80 dan 0.94 dengan saiz langkah 0.02, dan kedua-dua kaedah adalah yang terbaik 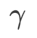 #🎜🎜 # ialah 0.88.
#🎜🎜 # ialah 0.88.
Anehnya, seperti yang ditunjukkan dalam Tab 7, garis dasar WSAM menunjukkan generalisasi yang lebih baik walaupun di kalangan berbilang calon. Oleh itu, kami mengesyorkan terus menggunakan WSAM dengan garis dasar 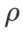 tetap.
tetap.

Eksperimen Ablasi#🎟#🎜🎜🎜🎜🎜🎜🎜 ini Kami menjalankan eksperimen ablasi untuk mendapatkan pemahaman yang lebih mendalam tentang kepentingan teknik "penyahgandingan berat" dalam WSAM. Seperti yang diterangkan dalam butiran reka bentuk WSAM, kami membandingkan varian WSAM tanpa "penyahgandingan berat" (Algoritma 4) Coupled-WSAM dengan kaedah asal.
Hasilnya ditunjukkan dalam Tab 8. Coupled-WSAM menghasilkan hasil yang lebih baik daripada SAM dalam kebanyakan kes, dan WSAM menambah baik lagi keputusan dalam kebanyakan kes, menunjukkan keberkesanan teknik "penyisihan gandingan berat".
Analisis titik ekstrem
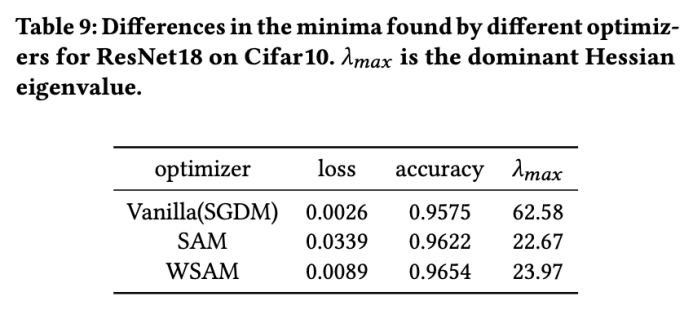
Di sini, kami memperdalam lagi pemahaman kami tentang pengoptimum WSAM dengan membandingkan perbezaan antara titik ekstrem yang ditemui oleh pengoptimum WSAM dan SAM. Kerataan (kecuraman) pada titik ekstrem boleh diterangkan oleh nilai eigen maksimum matriks Hessian. Semakin besar nilai eigen, semakin kurang rata. Kami menggunakan algoritma Lelaran Kuasa untuk mengira nilai eigen maksimum ini.
Tab 9 menunjukkan perbezaan antara titik ekstrem yang ditemui oleh pengoptimum SAM dan WSAM. Kami mendapati bahawa titik ekstrem yang ditemui oleh pengoptimum vanila mempunyai nilai kerugian yang lebih kecil tetapi kurang rata, manakala titik ekstrem yang ditemui oleh SAM mempunyai nilai kerugian yang lebih besar tetapi lebih rata, sekali gus meningkatkan prestasi generalisasi. Menariknya, titik ekstrem yang ditemui oleh WSAM bukan sahaja mempunyai nilai kerugian yang jauh lebih kecil daripada SAM, tetapi juga mempunyai kerataan yang sangat hampir dengan SAM. Ini menunjukkan bahawa dalam proses mencari titik ekstrem, WSAM mengutamakan memastikan nilai kerugian yang lebih kecil semasa cuba mencari kawasan yang lebih rata.
Sensitiviti Hiperparameter
Berbanding SAM, WSAM mempunyai hiperparameter tambahan 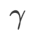 untuk menskalakan saiz istilah darjah rata (curam). Di sini, kami menguji sensitiviti prestasi generalisasi WSAM kepada hiperparameter ini. Kami melatih model ResNet18 dan WRN-28-10 menggunakan WSAM pada Cifar10 dan Cifar100, menggunakan pelbagai nilai
untuk menskalakan saiz istilah darjah rata (curam). Di sini, kami menguji sensitiviti prestasi generalisasi WSAM kepada hiperparameter ini. Kami melatih model ResNet18 dan WRN-28-10 menggunakan WSAM pada Cifar10 dan Cifar100, menggunakan pelbagai nilai 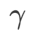 . Seperti yang ditunjukkan dalam Rajah 3, keputusan menunjukkan bahawa WSAM tidak sensitif terhadap pilihan hiperparameter
. Seperti yang ditunjukkan dalam Rajah 3, keputusan menunjukkan bahawa WSAM tidak sensitif terhadap pilihan hiperparameter 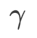 . Kami juga mendapati bahawa prestasi generalisasi optimum WSAM hampir selalu antara 0.8 dan 0.95.
. Kami juga mendapati bahawa prestasi generalisasi optimum WSAM hampir selalu antara 0.8 dan 0.95.
Atas ialah kandungan terperinci Lebih serba boleh dan berkesan, WSAM pengoptimum yang dibangunkan sendiri oleh Ant telah dipilih ke dalam KDD Oral. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

AI Hentai Generator
Menjana ai hentai secara percuma.

Artikel Panas

Alat panas

Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma

SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan

Hantar Studio 13.0.1
Persekitaran pembangunan bersepadu PHP yang berkuasa

Dreamweaver CS6
Alat pembangunan web visual

SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)

Topik panas
 1374
1374
 52
52
 Gunakan ddrescue untuk memulihkan data pada Linux
Mar 20, 2024 pm 01:37 PM
Gunakan ddrescue untuk memulihkan data pada Linux
Mar 20, 2024 pm 01:37 PM
DDREASE ialah alat untuk memulihkan data daripada fail atau peranti sekat seperti cakera keras, SSD, cakera RAM, CD, DVD dan peranti storan USB. Ia menyalin data dari satu peranti blok ke peranti lain, meninggalkan blok data yang rosak dan hanya memindahkan blok data yang baik. ddreasue ialah alat pemulihan yang berkuasa yang automatik sepenuhnya kerana ia tidak memerlukan sebarang gangguan semasa operasi pemulihan. Selain itu, terima kasih kepada fail peta ddasue, ia boleh dihentikan dan disambung semula pada bila-bila masa. Ciri-ciri utama lain DDREASE adalah seperti berikut: Ia tidak menimpa data yang dipulihkan tetapi mengisi jurang sekiranya pemulihan berulang. Walau bagaimanapun, ia boleh dipotong jika alat itu diarahkan untuk melakukannya secara eksplisit. Pulihkan data daripada berbilang fail atau blok kepada satu
 Sumber terbuka! Di luar ZoeDepth! DepthFM: Anggaran kedalaman monokular yang cepat dan tepat!
Apr 03, 2024 pm 12:04 PM
Sumber terbuka! Di luar ZoeDepth! DepthFM: Anggaran kedalaman monokular yang cepat dan tepat!
Apr 03, 2024 pm 12:04 PM
0. Apakah fungsi artikel ini? Kami mencadangkan DepthFM: model anggaran kedalaman monokular generatif yang serba boleh dan pantas. Sebagai tambahan kepada tugas anggaran kedalaman tradisional, DepthFM juga menunjukkan keupayaan terkini dalam tugas hiliran seperti mengecat kedalaman. DepthFM cekap dan boleh mensintesis peta kedalaman dalam beberapa langkah inferens. Mari kita baca karya ini bersama-sama ~ 1. Tajuk maklumat kertas: DepthFM: FastMonocularDepthEstimationwithFlowMatching Pengarang: MingGui, JohannesS.Fischer, UlrichPrestel, PingchuanMa, Dmytr
 Hello, Atlas elektrik! Robot Boston Dynamics hidup semula, gerakan pelik 180 darjah menakutkan Musk
Apr 18, 2024 pm 07:58 PM
Hello, Atlas elektrik! Robot Boston Dynamics hidup semula, gerakan pelik 180 darjah menakutkan Musk
Apr 18, 2024 pm 07:58 PM
Boston Dynamics Atlas secara rasmi memasuki era robot elektrik! Semalam, Atlas hidraulik hanya "menangis" menarik diri daripada peringkat sejarah Hari ini, Boston Dynamics mengumumkan bahawa Atlas elektrik sedang berfungsi. Nampaknya dalam bidang robot humanoid komersial, Boston Dynamics berazam untuk bersaing dengan Tesla. Selepas video baharu itu dikeluarkan, ia telah pun ditonton oleh lebih sejuta orang dalam masa sepuluh jam sahaja. Orang lama pergi dan peranan baru muncul. Ini adalah keperluan sejarah. Tidak dinafikan bahawa tahun ini adalah tahun letupan robot humanoid. Netizen mengulas: Kemajuan robot telah menjadikan majlis pembukaan tahun ini kelihatan seperti manusia, dan tahap kebebasan adalah jauh lebih besar daripada manusia Tetapi adakah ini benar-benar bukan filem seram? Pada permulaan video, Atlas berbaring dengan tenang di atas tanah, seolah-olah terlentang. Apa yang berikut adalah rahang-jatuh
 Google gembira: prestasi JAX mengatasi Pytorch dan TensorFlow! Ia mungkin menjadi pilihan terpantas untuk latihan inferens GPU
Apr 01, 2024 pm 07:46 PM
Google gembira: prestasi JAX mengatasi Pytorch dan TensorFlow! Ia mungkin menjadi pilihan terpantas untuk latihan inferens GPU
Apr 01, 2024 pm 07:46 PM
Prestasi JAX, yang dipromosikan oleh Google, telah mengatasi Pytorch dan TensorFlow dalam ujian penanda aras baru-baru ini, menduduki tempat pertama dalam 7 penunjuk. Dan ujian tidak dilakukan pada TPU dengan prestasi JAX terbaik. Walaupun dalam kalangan pembangun, Pytorch masih lebih popular daripada Tensorflow. Tetapi pada masa hadapan, mungkin lebih banyak model besar akan dilatih dan dijalankan berdasarkan platform JAX. Model Baru-baru ini, pasukan Keras menanda aras tiga hujung belakang (TensorFlow, JAX, PyTorch) dengan pelaksanaan PyTorch asli dan Keras2 dengan TensorFlow. Pertama, mereka memilih satu set arus perdana
 Kelajuan Internet Data Selular Perlahan pada iPhone: Pembetulan
May 03, 2024 pm 09:01 PM
Kelajuan Internet Data Selular Perlahan pada iPhone: Pembetulan
May 03, 2024 pm 09:01 PM
Menghadapi ketinggalan, sambungan data mudah alih perlahan pada iPhone? Biasanya, kekuatan internet selular pada telefon anda bergantung pada beberapa faktor seperti rantau, jenis rangkaian selular, jenis perayauan, dsb. Terdapat beberapa perkara yang boleh anda lakukan untuk mendapatkan sambungan Internet selular yang lebih pantas dan boleh dipercayai. Betulkan 1 – Paksa Mulakan Semula iPhone Kadangkala, paksa memulakan semula peranti anda hanya menetapkan semula banyak perkara, termasuk sambungan selular. Langkah 1 – Hanya tekan kekunci naikkan kelantangan sekali dan lepaskan. Seterusnya, tekan kekunci Turun Kelantangan dan lepaskannya semula. Langkah 2 - Bahagian seterusnya proses adalah untuk menahan butang di sebelah kanan. Biarkan iPhone selesai dimulakan semula. Dayakan data selular dan semak kelajuan rangkaian. Semak semula Betulkan 2 – Tukar mod data Walaupun 5G menawarkan kelajuan rangkaian yang lebih baik, ia berfungsi lebih baik apabila isyarat lemah
 Daya hidup kecerdasan super membangkitkan! Tetapi dengan kedatangan AI yang mengemas kini sendiri, ibu tidak perlu lagi bimbang tentang kesesakan data
Apr 29, 2024 pm 06:55 PM
Daya hidup kecerdasan super membangkitkan! Tetapi dengan kedatangan AI yang mengemas kini sendiri, ibu tidak perlu lagi bimbang tentang kesesakan data
Apr 29, 2024 pm 06:55 PM
Saya menangis hingga mati. Dunia sedang membina model besar. Data di Internet tidak mencukupi. Model latihan kelihatan seperti "The Hunger Games", dan penyelidik AI di seluruh dunia bimbang tentang cara memberi makan data ini kepada pemakan yang rakus. Masalah ini amat ketara dalam tugas berbilang modal. Pada masa mereka mengalami kerugian, pasukan pemula dari Jabatan Universiti Renmin China menggunakan model baharu mereka sendiri untuk menjadi yang pertama di China untuk menjadikan "suapan data yang dijana model itu sendiri" menjadi kenyataan. Selain itu, ia merupakan pendekatan serampang dua mata dari segi pemahaman dan sisi penjanaan Kedua-dua pihak boleh menjana data baharu berbilang modal yang berkualiti tinggi dan memberikan maklum balas data kepada model itu sendiri. Apakah model? Awaker 1.0, model berbilang modal besar yang baru sahaja muncul di Forum Zhongguancun. Siapa pasukan itu? Enjin Sophon. Diasaskan oleh Gao Yizhao, pelajar kedoktoran di Sekolah Kecerdasan Buatan Hillhouse Universiti Renmin.
 Versi Kuaishou Sora 'Ke Ling' dibuka untuk ujian: menghasilkan video lebih 120-an, memahami fizik dengan lebih baik dan boleh memodelkan pergerakan kompleks dengan tepat
Jun 11, 2024 am 09:51 AM
Versi Kuaishou Sora 'Ke Ling' dibuka untuk ujian: menghasilkan video lebih 120-an, memahami fizik dengan lebih baik dan boleh memodelkan pergerakan kompleks dengan tepat
Jun 11, 2024 am 09:51 AM
Apa? Adakah Zootopia dibawa menjadi realiti oleh AI domestik? Didedahkan bersama-sama dengan video itu ialah model penjanaan video domestik berskala besar baharu yang dipanggil "Keling". Sora menggunakan laluan teknikal yang serupa dan menggabungkan beberapa inovasi teknologi yang dibangunkan sendiri untuk menghasilkan video yang bukan sahaja mempunyai pergerakan yang besar dan munasabah, tetapi juga mensimulasikan ciri-ciri dunia fizikal dan mempunyai keupayaan gabungan konsep dan imaginasi yang kuat. Mengikut data, Keling menyokong penjanaan video ultra panjang sehingga 2 minit pada 30fps, dengan resolusi sehingga 1080p dan menyokong berbilang nisbah aspek. Satu lagi perkara penting ialah Keling bukanlah demo atau demonstrasi hasil video yang dikeluarkan oleh makmal, tetapi aplikasi peringkat produk yang dilancarkan oleh Kuaishou, pemain terkemuka dalam bidang video pendek. Selain itu, tumpuan utama adalah untuk menjadi pragmatik, bukan untuk menulis cek kosong, dan pergi ke dalam talian sebaik sahaja ia dikeluarkan Model besar Ke Ling telah pun dikeluarkan di Kuaiying.
 Tentera Udara A.S. mempamerkan jet pejuang AI pertamanya dengan profil tinggi! Menteri secara peribadi menjalankan pandu uji tanpa campur tangan semasa keseluruhan proses, dan 100,000 baris kod telah diuji selama 21 kali.
May 07, 2024 pm 05:00 PM
Tentera Udara A.S. mempamerkan jet pejuang AI pertamanya dengan profil tinggi! Menteri secara peribadi menjalankan pandu uji tanpa campur tangan semasa keseluruhan proses, dan 100,000 baris kod telah diuji selama 21 kali.
May 07, 2024 pm 05:00 PM
Baru-baru ini, bulatan tentera telah terharu dengan berita: jet pejuang tentera AS kini boleh melengkapkan pertempuran udara automatik sepenuhnya menggunakan AI. Ya, baru-baru ini, jet pejuang AI tentera AS telah didedahkan buat pertama kali, mendedahkan misterinya. Nama penuh pesawat pejuang ini ialah Variable Stability Simulator Test Aircraft (VISTA). Ia diterbangkan sendiri oleh Setiausaha Tentera Udara AS untuk mensimulasikan pertempuran udara satu lawan satu. Pada 2 Mei, Setiausaha Tentera Udara A.S. Frank Kendall berlepas menggunakan X-62AVISTA di Pangkalan Tentera Udara Edwards Ambil perhatian bahawa semasa penerbangan selama satu jam, semua tindakan penerbangan telah diselesaikan secara autonomi oleh AI! Kendall berkata - "Sejak beberapa dekad yang lalu, kami telah memikirkan tentang potensi tanpa had pertempuran udara-ke-udara autonomi, tetapi ia sentiasa kelihatan di luar jangkauan." Namun kini,



