masyarakat
Belajar
Perpustakaan Alatan
Alat AI
Masa lapang
cari
Melayu
Jadual Kandungan
Dalam kertas terakhir, mereka membina jubin padat tunggal translasi bagi grid berdimensi tinggi
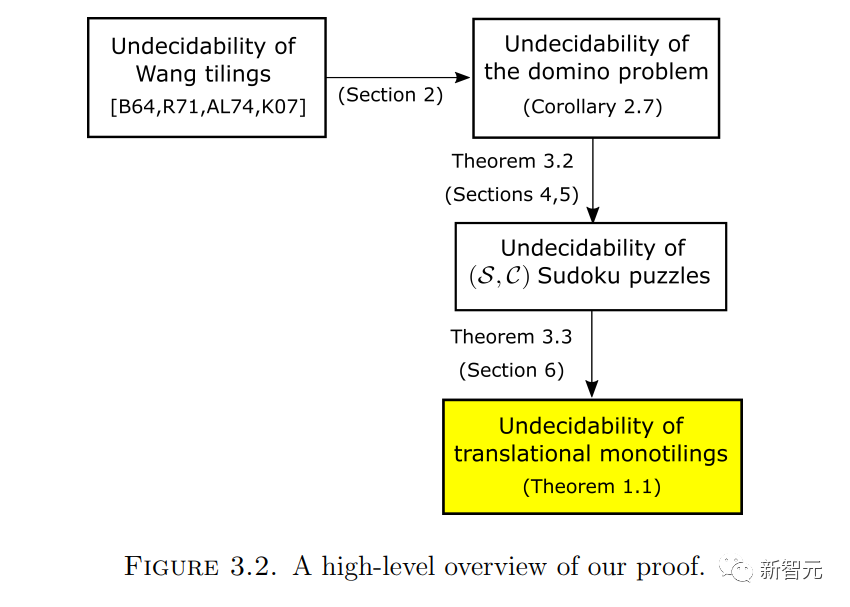
Rumah Peranti teknologi AI Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala

Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala

PHPz
PHPz
Oct 14, 2023 pm 02:17 PM
matematik masalah

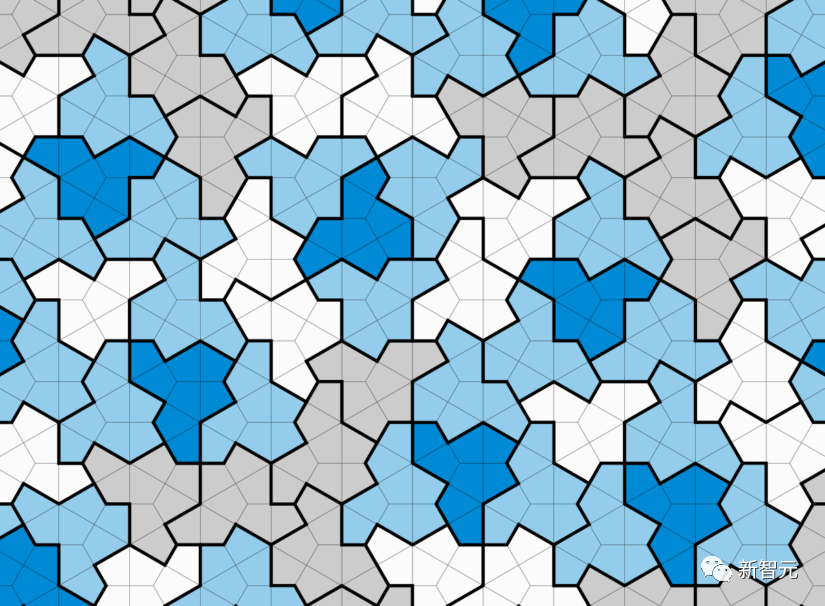
Tao Zhexuan membuat penemuan baharu dalam mengkaji masalah jubin berkala

Pada 18 September, Tao Zhexuan dan Rachel Greenfeld memuat naik kertas pracetak "Ketidakpastian monotiling translasi" Got to arXiv.

Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala

Alamat kertas: https://arxiv.org/abs/2309.09504

Kesimpulan utama kertas ini ialah jika dimensi grid tidak terhad, maka tentukan subbahagian grid terhingga Persoalan sama ada satu set boleh menjubinkan subset berkala grid tidak dapat diputuskan

Anda tahu, masalah ini boleh diputuskan dalam dimensi 1 dan dimensi 2.

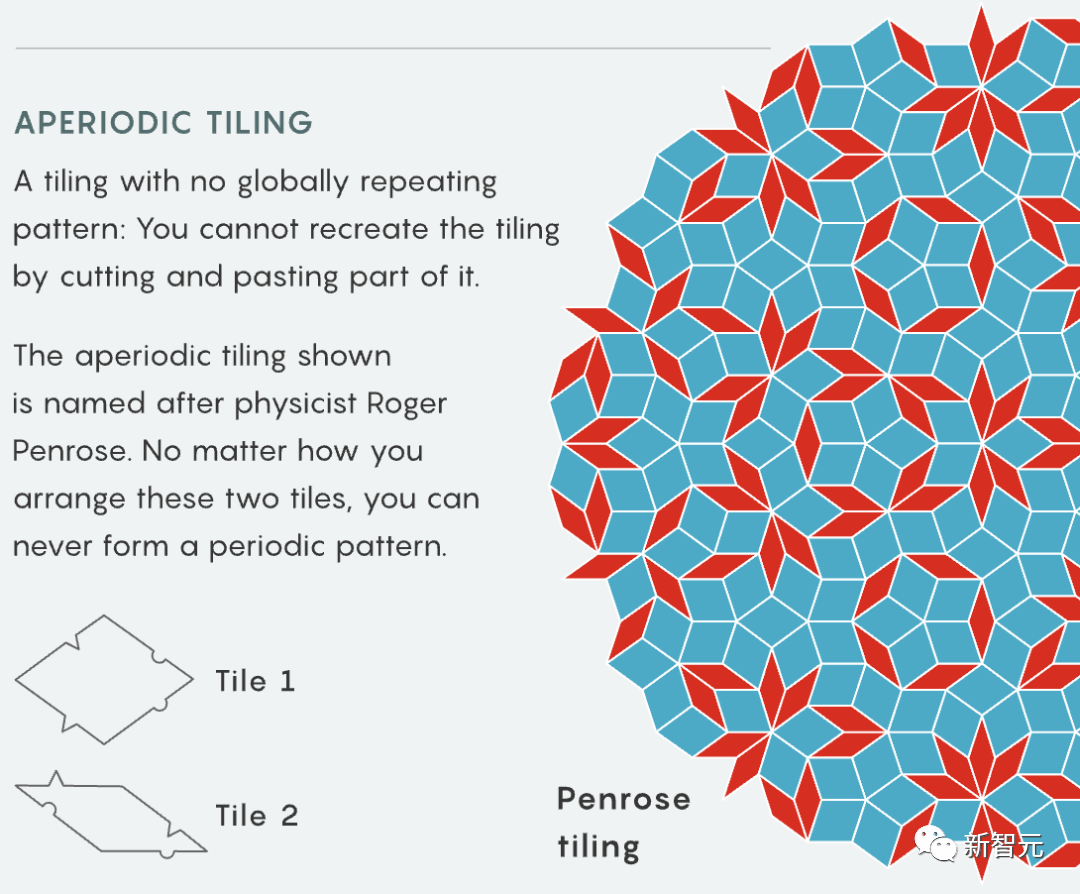
Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala

Tao Zhexuan berkata agak pelik bahawa kebanyakan komponen yang ditunjukkan dalam artikel itu serupa dengan permainan popular -

Analog jubin domino, Sudoku, permainan komputer "Tetris" " , malah permainan kanak-kanak "Fizz buzz" muncul

Mengapakah mempelajari masalah matematik melibatkan begitu banyak permainan? Tao Zhexuan juga tidak dapat menjelaskan ketidakpastian jubin padat tunggal translasi. Masalah Jubin Berkala Pautan

Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala

Dalam kertas terakhir, mereka membina jubin padat tunggal translasi bagi grid berdimensi tinggi

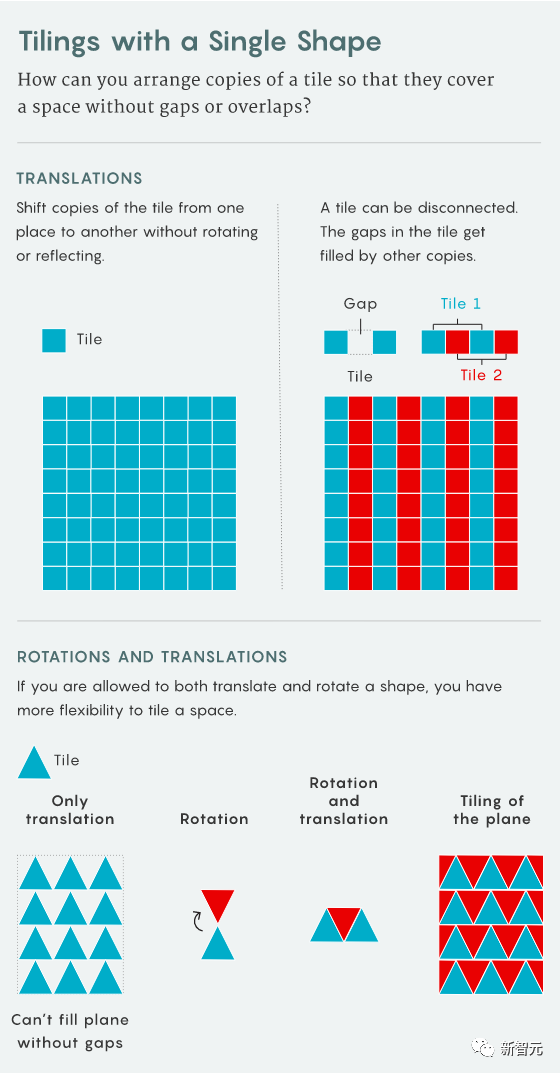
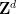Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala

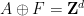
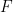Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala satu tiangTerence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala

set terhingga), ia bukan berkala (tiada cara untuk "membetulkan" jubin ini menjadi jubin berkala

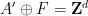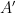
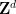
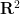
, di mana Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala kini berkala berkenaan dengan subkumpulan indeks terhingga Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala). Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkalaTerence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala

Fakta ini menafikan hipotesis Stein, Grunbaum-Shephard dan Lagarias-Wang tentang ketiadaan monomer padat aperiodik

Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala

Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala

Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala

🎜🎜🎜🎜🎜🎜🎜🎜🎜🎜🎜🎜🎜🎜🎜 baru-baru ini. jubin padat🎜🎜🎜, di mana putaran, pantulan dan terjemahan dibenarkan, atau "monolit hantu" yang lebih baharu adalah serupa dengan jubin padat tunggal topi, kecuali ia tidak diperlukan. 🎜🎜🎜🎜Salah satu sebab Tao Zhexuan dan Rachel Greenfeld mengilhamkan tekaan ini adalah pemerhatian ahli matematik Hao Wang 🎜🎜🎜🎜🎜🎜🎜 Dia mendapati bahawa jika tekaan jubin berkala adalah benar, maka masalah penyahjubinan berkala adalah benar ——🎜🎜

Ada mesin Turing, untuk 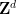Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala, apabila diberi dimensi 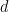Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala dan subset terhingga 🎜🎜#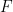Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala, anda boleh tentukan sama ada 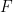Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala boleh ditutup untuk masa terhad. 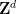Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkalaIni kerana jika terdapat turapan padat berkala, ia boleh didapati melalui carian komputer

#🎜🎜 # Sekiranya tiada turapan padat sama sekali, maka teorem kekompakan menunjukkan bahawa terdapat beberapa

subset yang tidak boleh

#🎜 🎜# Dilindungi oleh cerai terjemahan, ini juga boleh ditemui melalui carian komputer. 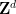Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkalaTekaan rahsia berkala menegaskan bahawa ini adalah satu-satunya dua situasi yang mungkin, sekali gus memberikan kebolehtetapan.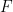 Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala

Sebaliknya, pandangan Wang tidak boleh diubah: kegagalan jangkaan turapan berkala tidak automatik bermakna ketidakpastian masalah jubin tunggal translasi, kerana ia tidak menolak kewujudan algoritma lain untuk menentukan jubin, yang boleh bebas daripada kewujudan jubin berkala

#🎜 🎜##🎜 🎜# (Sebagai contoh, walaupun dengan topi dan jubin hantu yang baru ditemui, adakah masalah jubin tunggal isometrik untuk poligon dengan pekali rasional dalam Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala

boleh diputuskan , masih menjadi persoalan terbuka, sama ada ia mempunyai renungan atau tidak. 🎜🎜##🎜🎜 # Tiada algoritma untuk

, diberi dimensi #🎜🎜 subset #🎜🎜, subset berkala 🎜# 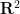Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala, dan subset terhad

, boleh menentukan sama ada terdapat jubin translasi dalam masa terhad #🎜 🎜 #.

Adalah penting untuk ambil perhatian bahawa seseorang mesti menggunakan subset berkala 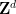Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala daripada Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala 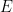daripada semua 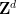Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala ini sebahagian besarnya disebabkan oleh batasan teknikal pendekatan ini dan mungkin dicapai dengan usaha dan kreativiti tambahan untuk menghapuskan.

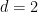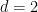Selain itu, Terence Tao dan Rachel Greenfeld juga menyedari bahawa apabila Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala, konjektur turapan berkala telah ditubuhkan oleh Bhattacharya, jadi masalahnya boleh diputuskan dalam kes ini Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala.

Untuk sebarang nilai tetap 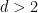Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala, ia masih terbuka sama ada masalah jubin boleh diputuskan (perhatikan bahawa dalam hasil di atas, dimensi 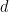Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala tidak tetap, tetapi sebahagian daripada input).

Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala

Disebabkan perkaitan yang terkenal antara ketidakpastian algoritma dan ketidakpastian logik (juga dikenali sebagai kebebasan logik), teorem ini juga membayangkan kewujudan dimensi (pada dasarnya tidak dapat dihuraikan dengan jelas) dimensi 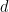Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala Subset berkala🜎 daripada , 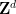Terence Tao menghampiri satu lagi masalah geometri 60 tahun! 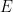Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala, dan subset terhingga Terence Tao menghampiri satu lagi masalah geometri 60 tahun! 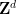Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala daripada Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala membuat 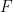Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala lulus jubin terjemahan 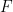Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala teori dan tidak boleh disahkan dalam kursus ZFC atau palsu.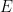 Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala

Sebagai hasil daripada pendekatan ini, kita juga boleh menggantikan

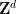di sini dengan kumpulan "hampir dua dimensi" Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala, di mana Terence Tao menghampiri satu lagi masalah geometri 60 tahun! 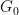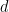Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala ialah kumpulan abelian terhingga, sebaliknya sebahagian daripada kumpulan Dimensi Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala). Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala

Seterusnya, huraikan beberapa idea utama pembuktian.

Cara biasa untuk membuktikan bahawa masalah tidak dapat diputuskan adalah dengan "mengekodkan" masalah lain yang diketahui tidak dapat diputuskan ke dalam masalah asal, supaya sebarang algoritma yang menentukan masalah asal juga boleh menentukan masalah terbenam

Oleh itu, kami mengekodkan masalah kedai padat Wang sebagai masalah kedai padat tunggal Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala:

Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala

Masalah kedua ialah mengenai masalah kedai padat Wang Wang

Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala set jubin Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala (segi empat unit, setiap tepi diberikan warna tertentu daripada palet terhad), adakah mungkin untuk merangkai satah menggunakan grid standard

Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala melalui terjemahan supaya jubin bersebelahan Mempunyai warna yang sama pada jubin biasa tepi? Berger pernah membuat kesimpulan terkenal bahawa masalah ini tidak dapat ditentukan Masalah jubin padat tunggal terjemahan dimensi perlu menyelesaikan beberapa masalah perantaraan

Pertama sekali, kita boleh dengan mudah membenamkan masalah jubin padat Wang ke dalam masalah yang sama, yang kita panggil masalah domino:

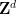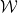Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala

Ditulis semula seperti berikut: Masalah domino ialah masalah 3

Diberi set terhingga domino mendatar (atau menegak)

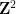atau Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala

, yang merupakan sepasang segi empat sama, setiap unit bersebelahan dengan titik elemen dalam set terhingga Adakah mungkin untuk menetapkan satu titik pada setiap unit persegi dalam jubin kekisi standard , supaya setiap pasangan dalam jubin ini Boleh petak mendatar (atau menegak) menggunakan domino dari

.

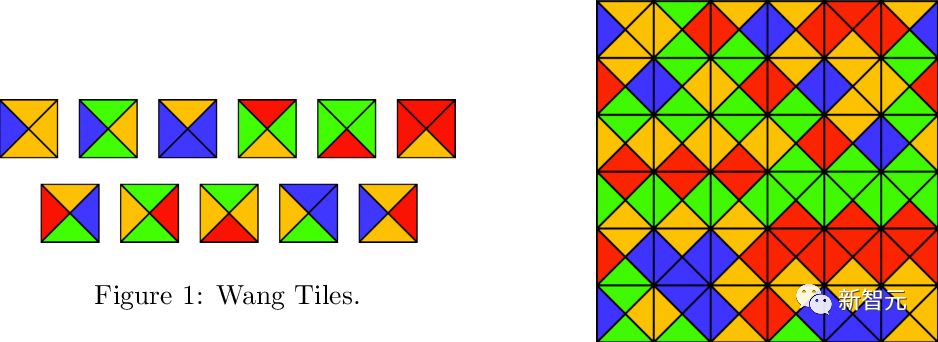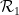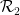
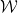atau Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala? Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkalaTerence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkalaSebenarnya, kita hanya perlu memasukkan setiap jubin Wang sebagai "titik" yang berasingan dan mentakrifkan set domino 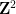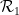Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala, Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala menjadi pasangan wang yang bersebelahan secara mendatar atau menegak, dengan tepi Wang yang bersebelahan. daripada warna yang sama.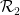 Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala

Dalam langkah seterusnya kami akan menggabungkan masalah domino dengan masalah Sudoku:

Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala.

dan "syarat awal" Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala . Adakah nombor

di sepanjang garis terletak di

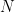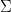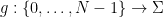
(dan Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala mematuhi syarat awal 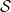Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala)? Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkalaTerence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkalaBahagian yang paling baru dalam kertas ini adalah untuk membuktikan bahawa masalah domino memang boleh diselitkan dalam masalah Sudoku.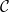 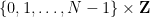Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkalaTerence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala Membenamkan masalah Sudoku ke dalam satu teka-teki rahsia adalah berdasarkan kaedah yang diubah suai yang dicadangkan dalam kertas sebelumnya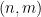Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkalaKertas ini juga mencadangkan versi berbeza masalah Sudoku dan mencipta kaedah yang dipanggil "teka-teki sifir" Kaedah " Bahasa Padding" boleh menukar pelbagai masalah (termasuk masalah Sudoku) kepada satu masalah paving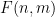Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkalaUntuk mengekod masalah domino menjadi masalah Sudoku, kita perlu mendapatkan fungsi domino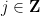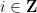Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkalaTerence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala( patuhi kekangan domino yang berkaitan dengan kekangan domino beberapa set domino 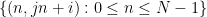Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala) dan gunakannya untuk membina fungsi Sudoku 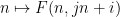Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala (patuhi beberapa kekangan Sudoku yang dikaitkan dengan set domino sebaliknya, masing-masing mematuhi nombor Fungsi Sudoku peraturan teka-teki Sudoku mesti dihasilkan daripada domino); berfungsi dalam beberapa cara.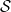 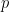Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala

Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala

Pendekatan ini tidak begitu jelas, tetapi Tao dan Rachel Greenfeld menyesuaikan beberapa idea daripada Aanderaa dan Lewis dengan bantuan Emmanuel Jeandel, dan hierarki tertentu digunakan untuk mengekod satu masalah kepada masalah yang lain.

Di sini kami menerangkan struktur hierarki Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala (disebabkan sifat dua dimensi masalah domino, dua nombor perdana berbeza perlu digunakan).

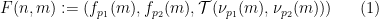Kemudian, bina fungsi Sudoku Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala dengan 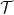Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala melalui formula 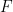Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala, yang akan merangkumi beberapa jenis benam.

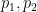di mana Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala ialah dua nombor perdana besar yang berbeza (contohnya, anda boleh mengambil 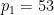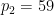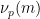Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala, Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala), Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala mewakili bilangan kali 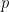Terence Tao menghampiri satu lagi masalah geometri 60 tahun! 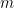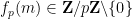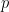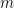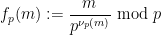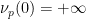Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala, dan dibahagi dengan Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala

ialah nombor bukan sifar terakhir dalam pengembangan Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala: Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkalaTerence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala

Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala (

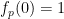
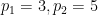), dan Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala Dalam kes 情况, komponen pertama (1) ditunjukkan di bawah: Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala

Contoh tipikal berat akhir Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala ditunjukkan di bawah: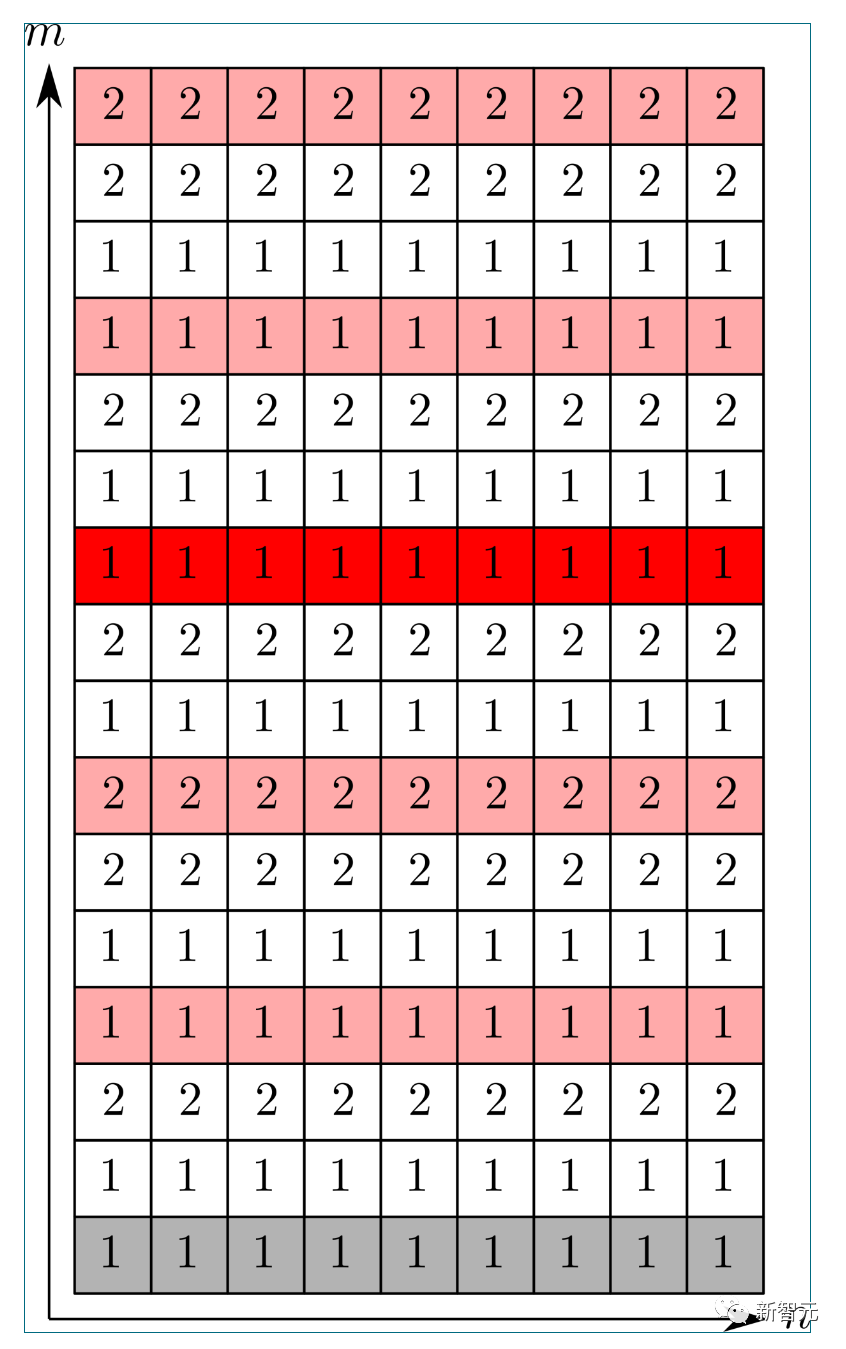

Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala

untuk beberapa sebab yang menarik , hiasan di sini pada asasnya mengikut peraturan permainan kanak-kanak "Fizz buzz"

Atas ialah kandungan terperinci Terence Tao menghampiri satu lagi masalah geometri 60 tahun! Satu kejayaan baru telah dibuat dalam masalah penurapan tertutup berkala. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

Kenyataan Laman Web ini
Kandungan artikel ini disumbangkan secara sukarela oleh netizen, dan hak cipta adalah milik pengarang asal. Laman web ini tidak memikul tanggungjawab undang-undang yang sepadan. Jika anda menemui sebarang kandungan yang disyaki plagiarisme atau pelanggaran, sila hubungi admin@php.cn

Alat AI Hot

Undresser.AI Undress

Undresser.AI Undress

Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover

AI Clothes Remover

Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool

Undress AI Tool

Gambar buka pakaian secara percuma

Clothoff.io

Clothoff.io

Penyingkiran pakaian AI

AI Hentai Generator

AI Hentai Generator

Menjana ai hentai secara percuma.

Tunjukkan Lagi

Artikel Panas

R.E.P.O. Kristal tenaga dijelaskan dan apa yang mereka lakukan (kristal kuning)
1 bulan yang lalu By 尊渡假赌尊渡假赌尊渡假赌
R.E.P.O. Tetapan grafik terbaik
1 bulan yang lalu By 尊渡假赌尊渡假赌尊渡假赌
Assassin's Creed Shadows: Penyelesaian Riddle Seashell
2 minggu yang lalu By DDD
R.E.P.O. Cara Memperbaiki Audio Jika anda tidak dapat mendengar sesiapa
1 bulan yang lalu By 尊渡假赌尊渡假赌尊渡假赌
R.E.P.O. Arahan sembang dan cara menggunakannya
1 bulan yang lalu By 尊渡假赌尊渡假赌尊渡假赌
Tunjukkan Lagi

Alat panas

Notepad++7.3.1

Notepad++7.3.1

Editor kod yang mudah digunakan dan percuma

SublimeText3 versi Cina

SublimeText3 versi Cina

Versi Cina, sangat mudah digunakan

Hantar Studio 13.0.1

Hantar Studio 13.0.1

Persekitaran pembangunan bersepadu PHP yang berkuasa

Dreamweaver CS6

Dreamweaver CS6

Alat pembangunan web visual

SublimeText3 versi Mac

SublimeText3 versi Mac

Perisian penyuntingan kod peringkat Tuhan (SublimeText3)

Tunjukkan Lagi

Topik panas

Di manakah pintu masuk log masuk untuk e-mel gmail?
7536
15
Tutorial CakePHP
1379
52
Apakah format nama akaun stim
82
11
kunci pengaktifan win11 kekal
55
19
Sambungan NYT menunjukkan dan jawapan
21
86
Tunjukkan Lagi
Related knowledge
Apr 09, 2024 am 11:52 AM

AI memang mengubah matematik. Baru-baru ini, Tao Zhexuan, yang telah mengambil perhatian terhadap isu ini, telah memajukan keluaran terbaru "Buletin Persatuan Matematik Amerika" (Buletin Persatuan Matematik Amerika). Memfokuskan pada topik "Adakah mesin akan mengubah matematik?", ramai ahli matematik menyatakan pendapat mereka Seluruh proses itu penuh dengan percikan api, tegar dan menarik. Penulis mempunyai barisan yang kuat, termasuk pemenang Fields Medal Akshay Venkatesh, ahli matematik China Zheng Lejun, saintis komputer NYU Ernest Davis dan ramai lagi sarjana terkenal dalam industri. Dunia AI telah berubah secara mendadak Anda tahu, banyak artikel ini telah dihantar setahun yang lalu.

nombor heptagon nombor heptagon Sep 24, 2023 am 10:33 AM

Nombor Aheptagonalberisannomboryang boleh diwakili sebagaiheptagon.Aheptagonisapolygondengan7sisi.Nombor Aheptagonalbolehdiwakilisebagaigabunganpelapisberturutandariheptagon(7 segipoligon).Nombor heptagonalbolehditerangkan dengan lebih baikdengan angka di bawah. oleh itu,

Algoritma CVM terobosan menyelesaikan lebih daripada 40 tahun masalah pengiraan! Saintis komputer membelek syiling untuk mengetahui perkataan unik untuk 'Hamlet' Algoritma CVM terobosan menyelesaikan lebih daripada 40 tahun masalah pengiraan! Saintis komputer membelek syiling untuk mengetahui perkataan unik untuk 'Hamlet' Jun 07, 2024 pm 03:44 PM

Mengira kedengaran mudah, tetapi sangat sukar untuk dilaksanakan dalam amalan. Bayangkan anda diangkut ke hutan hujan tropika yang asli untuk menjalankan banci hidupan liar. Setiap kali anda melihat haiwan, ambil gambar. Kamera digital hanya merekodkan jumlah bilangan haiwan yang dijejaki, tetapi anda berminat dengan bilangan haiwan unik, tetapi tiada statistik. Jadi apakah cara terbaik untuk mengakses populasi haiwan yang unik ini? Pada ketika ini, anda mesti berkata, mula mengira sekarang dan akhirnya bandingkan setiap spesies baharu daripada foto ke senarai. Walau bagaimanapun, kaedah pengiraan biasa ini kadangkala tidak sesuai untuk jumlah maklumat sehingga berbilion-bilion penyertaan. Para saintis komputer dari Institut Statistik India, UNL, dan Universiti Nasional Singapura telah mencadangkan algoritma baharu - CVM. Ia boleh menganggarkan pengiraan item yang berbeza dalam senarai panjang.

MLP dibunuh semalaman! MIT Caltech dan KAN revolusioner lain memecahkan rekod dan menemui teorem matematik yang menghancurkan DeepMind MLP dibunuh semalaman! MIT Caltech dan KAN revolusioner lain memecahkan rekod dan menemui teorem matematik yang menghancurkan DeepMind May 06, 2024 pm 03:10 PM

Sekelip mata, paradigma pembelajaran mesin akan berubah! Hari ini, infrastruktur yang mendominasi bidang pembelajaran mendalam ialah multilayer perceptron (MLP), yang meletakkan fungsi pengaktifan pada neuron. Jadi, selain daripada itu, adakah laluan baharu yang boleh kita lalui? Hari ini, pasukan dari MIT, Caltech, Universiti Timur Laut dan institusi lain mengeluarkan struktur rangkaian saraf baharu-Kolmogorov–Arnold Networks (KAN). Para penyelidik membuat perubahan mudah kepada MLP dengan mengalihkan fungsi pengaktifan yang boleh dipelajari daripada nod (neuron) ke tepi (berat)! Alamat kertas: https://arxiv.org/pdf/2404.19756 Perubahan ini kelihatan tidak berasas pada pandangan pertama

Adakah lukisan AI masih perlu tahu matematik? Adakah lukisan AI masih perlu tahu matematik? Jun 12, 2023 pm 02:05 PM

Visi Dengan perkembangan teknologi kecerdasan buatan, lukisan AI telah menjadi topik hangat pada masa ini. Dengan menggunakan algoritma pembelajaran mendalam, kecerdasan buatan boleh menjana imej realistik untuk mencipta karya seni yang menakjubkan. Di sebalik karya-karya menakjubkan ini, ia tidak dapat dipisahkan daripada sokongan pengetahuan matematik. Model matematik memainkan peranan penting dalam lukisan AI. Di satu pihak, model matematik digunakan untuk menerangkan dan mewakili maklumat imej, membolehkan komputer memahami dan memproses imej. Sebaliknya, model matematik juga digunakan untuk melatih model pembelajaran mendalam untuk mencapai penjanaan imej automatik. Model pembelajaran mendalam membawa penjanaan imej berkualiti tinggi Model pembelajaran mendalam adalah bahagian teras lukisan AI. Ia mengenal pasti dan mensimulasikan ciri-ciri imej dengan mempelajari sejumlah besar data imej, dan melalui pemprosesan data berbilang peringkat

Adakah matematik di sebalik model resapan terlalu sukar untuk dihadam? Google menjelaskannya dengan perspektif yang bersatu Adakah matematik di sebalik model resapan terlalu sukar untuk dihadam? Google menjelaskannya dengan perspektif yang bersatu Apr 11, 2023 pm 07:46 PM

Sejak kebelakangan ini, lukisan AI sangat popular. Walaupun anda kagum dengan keupayaan lukisan AI, apa yang anda mungkin tidak tahu ialah model resapan memainkan peranan yang besar di dalamnya. Ambil model OpenAI's DALL·E 2 sebagai contoh Hanya masukkan teks ringkas (prompt) dan ia boleh menjana berbilang imej definisi tinggi 1024*1024. Tidak lama selepas DALL·E 2 diumumkan, Google kemudiannya mengeluarkan Imagen, model AI teks-ke-imej yang boleh menjana imej realistik tempat kejadian daripada penerangan teks yang diberikan. Hanya beberapa hari yang lalu, Stability.Ai mengeluarkan model imej penjanaan teks Stable Diffusi secara terbuka

'Noob Matematik' ChatGPT memahami pilihan manusia dengan baik! Menjana nombor rawak dalam talian adalah jawapan muktamad kepada alam semesta 'Noob Matematik' ChatGPT memahami pilihan manusia dengan baik! Menjana nombor rawak dalam talian adalah jawapan muktamad kepada alam semesta Apr 01, 2023 am 11:48 AM

ChatGPT juga memahami helah manusia apabila ia datang untuk menjana nombor rawak. ChatGPT mungkin artis omong kosong dan penyebar maklumat salah, tetapi ia bukan "ahli matematik"! Baru-baru ini, Colin Fraser, seorang saintis data Meta, mendapati bahawa ChatGPT tidak boleh menjana nombor rawak yang benar-benar rawak, tetapi lebih seperti "nombor rawak manusia." Melalui eksperimen, Fraser membuat kesimpulan: "ChatGPT sangat menyukai nombor 42 dan 7. Netizen mengatakan bahawa ini bermakna manusia sangat menyukai nombor ini. ChatGPT juga menyukai "Jawapan Tertinggi kepada Alam Semesta". Dalam ujiannya, gesaan yang dimasukkan oleh Fraser adalah seperti berikut: "Pilih nombor rawak

Bekerja pada waktu siang dan melakukan penyelidikan pada waktu malam, saintis penyelidikan Google Brain menyelesaikan satu tekaan yang membingungkan komuniti matematik selama beberapa dekad. Bekerja pada waktu siang dan melakukan penyelidikan pada waktu malam, saintis penyelidikan Google Brain menyelesaikan satu tekaan yang membingungkan komuniti matematik selama beberapa dekad. Apr 12, 2023 am 09:49 AM

Pada pertengahan Oktober 2022, Justin Gilmer terbang dari California ke New York untuk melawat bekas mentornya Michael Saks, seorang ahli matematik di Universiti Rutgers, di Pantai Timur. Semasa mengenangkan, mereka tidak bercakap tentang matematik. Malah, Gilmer tidak memikirkan secara serius tentang matematik sejak memperoleh PhD di Universiti Rutgers pada 2015. Pada masa itu, dia memutuskan untuk tidak meneruskan kerjaya dalam bidang akademik dan mula mengajar dirinya pengaturcaraan. Semasa makan malam bersama Saks, Gilmer memberitahu mentornya tentang kerjanya di Google: pembelajaran mesin dan kecerdasan buatan. Semasa dia berjalan di sepanjang laluan di kampus, Gilmer teringat bahawa pada tahun 2013, dia menghabiskan lebih daripada setahun berjalan di laluan ini.

See all articles