 Peranti teknologi
Peranti teknologi
 AI
AI
 Meneroka Sejarah dan Matriks Kepintaran Buatan: Tutorial Kepintaran Buatan (2)
Meneroka Sejarah dan Matriks Kepintaran Buatan: Tutorial Kepintaran Buatan (2)
Meneroka Sejarah dan Matriks Kepintaran Buatan: Tutorial Kepintaran Buatan (2)

Dalam artikel pertama siri ini, kami membincangkan hubungan dan perbezaan antara kecerdasan buatan, pembelajaran mesin, pembelajaran mendalam, sains data dan bidang lain. Kami juga membuat beberapa pilihan sukar tentang bahasa pengaturcaraan, alatan dan banyak lagi yang akan digunakan oleh keseluruhan siri. Akhirnya, kami juga memperkenalkan sedikit ilmu matriks. Dalam artikel ini, kita akan membincangkan secara mendalam matriks, teras kecerdasan buatan. Tetapi sebelum itu, mari kita fahami dahulu sejarah kecerdasan buatan
Mengapa kita perlu memahami sejarah kecerdasan buatan? Terdapat banyak ledakan AI dalam sejarah, tetapi dalam banyak kes jangkaan besar untuk potensi AI gagal menjadi kenyataan. Memahami sejarah kecerdasan buatan boleh membantu kita melihat sama ada gelombang kecerdasan buatan ini akan mencipta keajaiban atau hanya gelembung lain yang akan pecah.
Bilakah kita mula memahami asal usul kecerdasan buatan? Adakah selepas penciptaan komputer digital? Atau lebih awal? Saya percaya mengejar makhluk yang maha mengetahui kembali kepada permulaan tamadun. Sebagai contoh, Delphi dalam mitologi Yunani kuno adalah seorang nabi yang boleh menjawab sebarang soalan. Pencarian mesin kreatif yang mengatasi kecerdasan manusia juga telah menarik perhatian kita sejak zaman purba. Terdapat beberapa percubaan yang gagal untuk membina mesin catur sepanjang sejarah. Antaranya ialah Mechanical Turk yang terkenal, yang bukan robot sebenar tetapi dikawal oleh pemain catur yang tersembunyi di dalamnya. Logaritma yang dicipta oleh John Napier, kalkulator Blaise Pascal dan Enjin Analitik Charles Babbage semuanya memainkan peranan penting dalam pembangunan kecerdasan buatan
Jadi, kecerdasan buatan Apakah peristiwa penting dalam perkembangannya setakat ini? Seperti yang dinyatakan sebelum ini, penciptaan komputer digital adalah peristiwa terpenting dalam sejarah penyelidikan kecerdasan buatan. Tidak seperti peranti elektromekanikal, yang berskala bergantung pada keperluan kuasa, peranti digital mendapat manfaat daripada kemajuan teknologi, seperti daripada tiub vakum kepada transistor kepada litar bersepadu dan kini VLSI.
Satu lagi peristiwa penting dalam pembangunan kecerdasan buatan ialah analisis teori pertama Alan Turing tentang kecerdasan buatan. Beliau mencadangkan ujian Turing yang terkenal
Pada akhir 1950-an, John McCarthy
Menjelang 1970-an dan 1980-an, algoritma memainkan peranan utama dalam tempoh ini memainkan peranan utama. Pada masa ini, banyak algoritma baru yang cekap telah dicadangkan. Pada akhir 1960-an, Donald Knuth (saya sangat mengesyorkan anda untuk mengenalinya, dalam dunia sains komputer, dia setara dengan Gauss atau Euler dalam dunia matematik) terkenal "The Art of Computer Programming" Penerbitan jilid pertama Pengaturcaraan menandakan permulaan era algoritma. Pada tahun-tahun ini, banyak algoritma tujuan umum dan algoritma graf telah dibangunkan. Selain itu, pengaturcaraan berasaskan rangkaian saraf tiruan juga muncul pada masa ini. Walaupun seawal tahun 1940-an, Warren S. McCulloch dan Walter Pitts
dalam era digital, kecerdasan buatan mempunyai sekurang-kurangnya dua peluang yang menjanjikan , tetapi kedua-dua peluang tidak dijangka. Adakah gelombang kecerdasan buatan semasa serupa dengan ini? Soalan ini sukar dijawab. Walau bagaimanapun, saya secara peribadi percaya bahawa kecerdasan buatan akan memberi impak yang besar kali ini (anotasi terjemahan LCTT: Artikel ini diterbitkan pada Jun 2022, ChatGTP telah dilancarkan setengah tahun kemudian). Mengapa saya mempunyai ramalan sedemikian? Pertama, peralatan pengkomputeran berprestasi tinggi kini murah dan mudah didapati. Pada tahun 1960-an atau 1980-an, terdapat hanya beberapa peranti pengkomputeran yang begitu berkuasa, sedangkan kini kita mempunyai berjuta-juta malah berbilion-bilion. Kedua, kini terdapat sejumlah besar data yang tersedia untuk melatih kecerdasan buatan dan program pembelajaran mesin. Bayangkan berapa ramai jurutera imej digital yang terlibat dalam pemprosesan imej digital pada 1990-an boleh gunakan untuk melatih algoritma? Mungkin beribu atau berpuluh ribu. Kini, platform sains data Kaggle (anak syarikat Google) sahaja mempunyai lebih daripada 10,000 set data. Sejumlah besar data yang dijana oleh Internet setiap hari menjadikannya lebih mudah untuk melatih algoritma. Ketiga, sambungan Internet berkelajuan tinggi memudahkan untuk bekerja dengan institusi besar. Dalam dekad pertama abad ke-21, kerjasama dalam kalangan saintis komputer adalah sukar. Walau bagaimanapun, kelajuan Internet kini menjadikan kerjasama dengan projek kecerdasan buatan seperti Google Colab, Kaggle dan Project Jupiter menjadi kenyataan. Berdasarkan tiga faktor ini, saya percaya bahawa kecerdasan buatan kali ini akan wujud selama-lamanya, dan akan ada banyak aplikasi yang sangat baik
Lebih banyak ilmu matriks
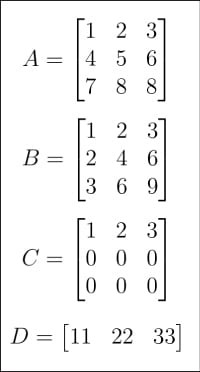 #🎜 🎜 #Rajah 1: Matriks A, B, C, D
#🎜 🎜 #Rajah 1: Matriks A, B, C, D
Setelah memahami sejarah kecerdasan buatan, kini tiba masanya untuk kembali kepada topik matriks dan vektor. Saya telah memperkenalkan mereka secara ringkas dalam artikel sebelum ini. Kali ini, kita akan mendalami dunia Matriks. Pertama, sila lihat Rajah 1 dan Rajah 2, yang menunjukkan sejumlah 8 matriks dari A hingga H. Mengapakah begitu banyak matriks diperlukan dalam kecerdasan buatan dan tutorial pembelajaran mesin? Pertama sekali, seperti yang dinyatakan sebelum ini, matriks ialah teras algebra linear, dan algebra linear bukanlah otak pembelajaran mesin, tetapi ia adalah teras pembelajaran mesin. Kedua, dalam perbincangan berikut, setiap matriks mempunyai tujuan tertentu
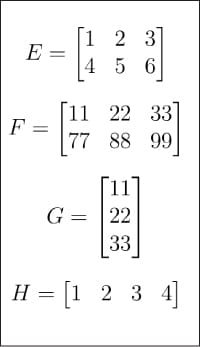 Rajah 2: Matriks E, F, G, H 🎜#Mari kita lihat bagaimana matriks diwakili dan cara mendapatkan butiran mereka. Rajah 3 menunjukkan cara mewakili matriks A menggunakan NumPy. Walaupun matriks dan tatasusunan tidak betul-betul sama, kami sering menggunakannya sebagai sinonim dalam aplikasi praktikal #
Rajah 2: Matriks E, F, G, H 🎜#Mari kita lihat bagaimana matriks diwakili dan cara mendapatkan butiran mereka. Rajah 3 menunjukkan cara mewakili matriks A menggunakan NumPy. Walaupun matriks dan tatasusunan tidak betul-betul sama, kami sering menggunakannya sebagai sinonim dalam aplikasi praktikal #
matriks berfungsi untuk mencipta tatasusunan dan matriks dua dimensi. Tetapi ia akan ditamatkan pada masa hadapan, jadi penggunaannya tidak lagi disyorkan. Beberapa butiran matriks A juga ditunjukkan dalam Rajah 3. A.size memberitahu kita bilangan elemen dalam tatasusunan. Dalam kes kami, ia adalah 9. Kod A.nidm mewakili dimensi tatasusunan. Adalah mudah untuk melihat bahawa matriks A adalah dua dimensi. A.shape mewakili susunan matriks A. Susunan matriks ialah bilangan baris dan lajur matriks. Walaupun saya tidak akan menerangkannya dengan lebih lanjut, anda perlu mengetahui saiz, dimensi dan susunan matriks anda apabila menggunakan perpustakaan NumPy. Rajah 4 menunjukkan mengapa saiz, dimensi dan susunan matriks perlu dikenal pasti dengan teliti. Perbezaan kecil dalam cara tatasusunan ditakrifkan boleh mengakibatkan perbezaan dalam saiz, dimensi dan susunannya. Oleh itu, pengaturcara harus memberi perhatian khusus kepada butiran ini apabila mentakrifkan matriks.
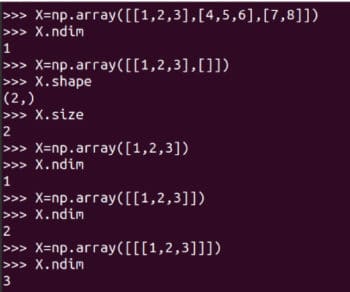
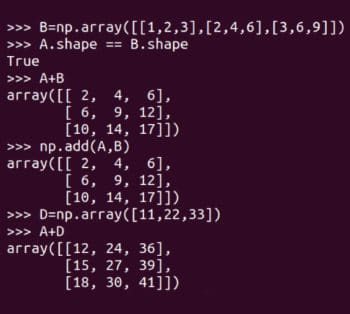
Rajah 4: Saiz, dimensi dan susunan tatasusunan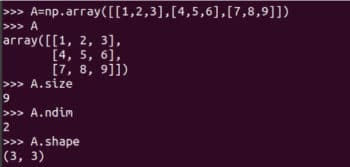 Sekarang kita melakukan beberapa operasi matriks asas. Rajah 5 menunjukkan bagaimana matriks A dan B ditambah. NumPy menyediakan dua kaedah untuk menambah matriks,
Sekarang kita melakukan beberapa operasi matriks asas. Rajah 5 menunjukkan bagaimana matriks A dan B ditambah. NumPy menyediakan dua kaedah untuk menambah matriks, tambah fungsi dan + operator. Ambil perhatian bahawa hanya matriks daripada susunan yang sama boleh ditambah. Sebagai contoh, dua matriks 4 × 3 boleh ditambah, tetapi matriks 3 × 4 dan matriks 2 × 3 tidak boleh ditambah. Walau bagaimanapun, kerana pengaturcaraan berbeza daripada matematik, NumPy sebenarnya tidak mengikut peraturan ini. Rajah 5 juga menunjukkan penambahan matriks A dan D. Ingat, penambahan matriks seperti ini adalah haram secara matematik. Satu dipanggil penyiaran penyiaran
array 函数创建矩阵。虽然 NumPy 也提供了 matrix 函数来创建二维数组和矩阵。但是它将在未来被废弃,所以不再建议使用了。在图 3 还显示了矩阵 A 的一些详细信息。A.size 告诉我们数组中元素的个数。在我们的例子中,它是 9。代码 A.nidm 表示数组的 维数dimension。很容易看出矩阵 A 是二维的。A.shape 表示矩阵 A 的阶数order,矩阵的阶数是矩阵的行数和列数。虽然我不会进一步解释,但使用 NumPy 库时需要注意矩阵的大小、维度和阶数。图 4 显示了为什么应该仔细识别矩阵的大小、维数和阶数。定义数组时的微小差异可能导致其大小、维数和阶数的不同。因此,程序员在定义矩阵时应该格外注意这些细节。
 图 4:数组的大小、维数和阶数
图 4:数组的大小、维数和阶数
现在我们来做一些基本的矩阵运算。图 5 显示了如何将矩阵 A 和 B 相加。NumPy 提供了两种方法将矩阵相加,add 函数和 +
 Re-ungkapan 5: Matriks penjumlahan Dan
Re-ungkapan 5: Matriks penjumlahan Dan
A.shape == B.shape
当然除了矩阵加法外还有其它矩阵运算。图 6 展示了矩阵减法和矩阵乘法。它们同样有两种形式,矩阵减法可以由 subtract 函数或减法运算符 - 来实现,矩阵乘法可以由 matmul 函数或矩阵乘法运算符 @ 来实现。图 6 还展示了 逐元素乘法element-wise multiplication 运算符 * 的使用。请注意,只有 NumPy 的 matmul 函数和 @ 运算符执行的是数学意义上的矩阵乘法。在处理矩阵时要小心使用 * 运算符。
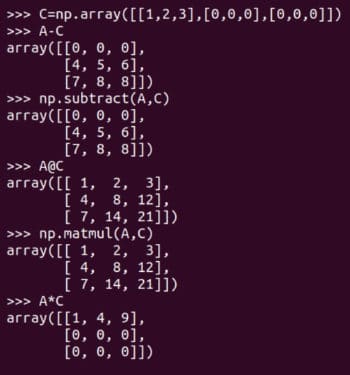 图 6:更多矩阵运算
图 6:更多矩阵运算
对于一个 m x n 阶和一个 p x q 阶的矩阵,当且仅当 n 等于 p 时它们才可以相乘,相乘的结果是一个 m x q 阶矩的阵。图 7 显示了更多矩阵相乘的示例。注意 E@A 是可行的,而 A@E 会导致错误。请仔细阅读对比 D@G 和 G@D 的示例。使用 shape 属性,确定这 8 个矩阵中哪些可以相乘。虽然根据严格的数学定义,矩阵是二维的,但我们将要处理更高维的数组。作为例子,下面的代码创建一个名为 T 的三维数组。
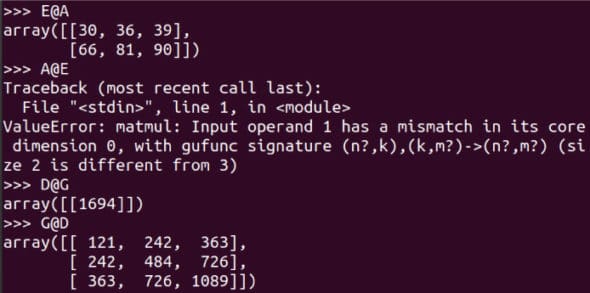 图 7:更多矩阵乘法的例子
图 7:更多矩阵乘法的例子
T = np.array([[[11,22], [33,44]], [[55,66], [77,88]]])
Pandas
到目前为止,我们都是通过键盘输入矩阵的。如果我们需要从文件或数据集中读取大型矩阵并处理,那该怎么办呢?这时我们就要用到另一个强大的 Python 库了——Pandas。我们以读取一个小的 CSV (逗号分隔值comma-separated value)文件为例。图 8 展示了如何读取 cricket.csv 文件,并将其中的前三行打印到终端上。在本系列的后续文章中将会介绍 Pandas 的更多特性。
 图 8:用 Pandas 读取 CSV 文件
图 8:用 Pandas 读取 CSV 文件
图 8:用 Pandas 读取 CSV 文件
矩阵的秩
需要进行改写的内容是:矩阵的秩
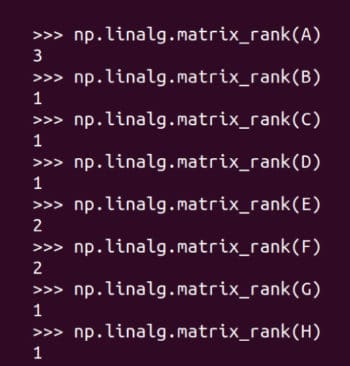 Rajah 9: Mencari pangkat matriks
Rajah 9: Mencari pangkat matriks
Ini adalah penghujung kandungan ini. Dalam artikel seterusnya, kami akan mengembangkan perpustakaan alatan supaya ia boleh digunakan untuk membangunkan kecerdasan buatan dan program pembelajaran mesin. Kami juga akan membincangkan rangkaian saraf, pembelajaran diselia dan pembelajaran tanpa pengawasan dengan lebih terperinci
Atas ialah kandungan terperinci Meneroka Sejarah dan Matriks Kepintaran Buatan: Tutorial Kepintaran Buatan (2). Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

AI Hentai Generator
Menjana ai hentai secara percuma.

Artikel Panas

Alat panas

Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma

SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan

Hantar Studio 13.0.1
Persekitaran pembangunan bersepadu PHP yang berkuasa

Dreamweaver CS6
Alat pembangunan web visual

SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)

Topik panas
 1377
1377
 52
52
 Bytedance Cutting melancarkan keahlian super SVIP: 499 yuan untuk langganan tahunan berterusan, menyediakan pelbagai fungsi AI
Jun 28, 2024 am 03:51 AM
Bytedance Cutting melancarkan keahlian super SVIP: 499 yuan untuk langganan tahunan berterusan, menyediakan pelbagai fungsi AI
Jun 28, 2024 am 03:51 AM
Laman web ini melaporkan pada 27 Jun bahawa Jianying ialah perisian penyuntingan video yang dibangunkan oleh FaceMeng Technology, anak syarikat ByteDance Ia bergantung pada platform Douyin dan pada asasnya menghasilkan kandungan video pendek untuk pengguna platform tersebut Windows , MacOS dan sistem pengendalian lain. Jianying secara rasmi mengumumkan peningkatan sistem keahliannya dan melancarkan SVIP baharu, yang merangkumi pelbagai teknologi hitam AI, seperti terjemahan pintar, penonjolan pintar, pembungkusan pintar, sintesis manusia digital, dsb. Dari segi harga, yuran bulanan untuk keratan SVIP ialah 79 yuan, yuran tahunan ialah 599 yuan (nota di laman web ini: bersamaan dengan 49.9 yuan sebulan), langganan bulanan berterusan ialah 59 yuan sebulan, dan langganan tahunan berterusan ialah 499 yuan setahun (bersamaan dengan 41.6 yuan sebulan) . Di samping itu, pegawai yang dipotong juga menyatakan bahawa untuk meningkatkan pengalaman pengguna, mereka yang telah melanggan VIP asal
 Pembantu pengekodan AI yang ditambah konteks menggunakan Rag dan Sem-Rag
Jun 10, 2024 am 11:08 AM
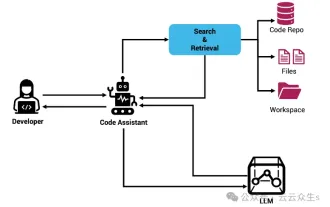
Pembantu pengekodan AI yang ditambah konteks menggunakan Rag dan Sem-Rag
Jun 10, 2024 am 11:08 AM
Tingkatkan produktiviti, kecekapan dan ketepatan pembangun dengan menggabungkan penjanaan dipertingkatkan semula dan memori semantik ke dalam pembantu pengekodan AI. Diterjemah daripada EnhancingAICodingAssistantswithContextUsingRAGandSEM-RAG, pengarang JanakiramMSV. Walaupun pembantu pengaturcaraan AI asas secara semulajadi membantu, mereka sering gagal memberikan cadangan kod yang paling relevan dan betul kerana mereka bergantung pada pemahaman umum bahasa perisian dan corak penulisan perisian yang paling biasa. Kod yang dijana oleh pembantu pengekodan ini sesuai untuk menyelesaikan masalah yang mereka bertanggungjawab untuk menyelesaikannya, tetapi selalunya tidak mematuhi piawaian pengekodan, konvensyen dan gaya pasukan individu. Ini selalunya menghasilkan cadangan yang perlu diubah suai atau diperhalusi agar kod itu diterima ke dalam aplikasi
 Bolehkah penalaan halus benar-benar membolehkan LLM mempelajari perkara baharu: memperkenalkan pengetahuan baharu boleh menjadikan model menghasilkan lebih banyak halusinasi
Jun 11, 2024 pm 03:57 PM
Bolehkah penalaan halus benar-benar membolehkan LLM mempelajari perkara baharu: memperkenalkan pengetahuan baharu boleh menjadikan model menghasilkan lebih banyak halusinasi
Jun 11, 2024 pm 03:57 PM
Model Bahasa Besar (LLM) dilatih pada pangkalan data teks yang besar, di mana mereka memperoleh sejumlah besar pengetahuan dunia sebenar. Pengetahuan ini dibenamkan ke dalam parameter mereka dan kemudiannya boleh digunakan apabila diperlukan. Pengetahuan tentang model ini "diperbaharui" pada akhir latihan. Pada akhir pra-latihan, model sebenarnya berhenti belajar. Selaraskan atau perhalusi model untuk mempelajari cara memanfaatkan pengetahuan ini dan bertindak balas dengan lebih semula jadi kepada soalan pengguna. Tetapi kadangkala pengetahuan model tidak mencukupi, dan walaupun model boleh mengakses kandungan luaran melalui RAG, ia dianggap berfaedah untuk menyesuaikan model kepada domain baharu melalui penalaan halus. Penalaan halus ini dilakukan menggunakan input daripada anotasi manusia atau ciptaan LLM lain, di mana model menemui pengetahuan dunia sebenar tambahan dan menyepadukannya
 Tujuh Soalan Temuduga Teknikal GenAI & LLM yang Cool
Jun 07, 2024 am 10:06 AM
Tujuh Soalan Temuduga Teknikal GenAI & LLM yang Cool
Jun 07, 2024 am 10:06 AM
Untuk mengetahui lebih lanjut tentang AIGC, sila layari: 51CTOAI.x Komuniti https://www.51cto.com/aigc/Translator|Jingyan Reviewer|Chonglou berbeza daripada bank soalan tradisional yang boleh dilihat di mana-mana sahaja di Internet memerlukan pemikiran di luar kotak. Model Bahasa Besar (LLM) semakin penting dalam bidang sains data, kecerdasan buatan generatif (GenAI) dan kecerdasan buatan. Algoritma kompleks ini meningkatkan kemahiran manusia dan memacu kecekapan dan inovasi dalam banyak industri, menjadi kunci kepada syarikat untuk kekal berdaya saing. LLM mempunyai pelbagai aplikasi Ia boleh digunakan dalam bidang seperti pemprosesan bahasa semula jadi, penjanaan teks, pengecaman pertuturan dan sistem pengesyoran. Dengan belajar daripada sejumlah besar data, LLM dapat menjana teks
 Untuk menyediakan tanda aras dan sistem penilaian menjawab soalan saintifik dan kompleks baharu untuk model besar, UNSW, Argonne, University of Chicago dan institusi lain bersama-sama melancarkan rangka kerja SciQAG
Jul 25, 2024 am 06:42 AM
Untuk menyediakan tanda aras dan sistem penilaian menjawab soalan saintifik dan kompleks baharu untuk model besar, UNSW, Argonne, University of Chicago dan institusi lain bersama-sama melancarkan rangka kerja SciQAG
Jul 25, 2024 am 06:42 AM
Editor |ScienceAI Question Answering (QA) set data memainkan peranan penting dalam mempromosikan penyelidikan pemprosesan bahasa semula jadi (NLP). Set data QA berkualiti tinggi bukan sahaja boleh digunakan untuk memperhalusi model, tetapi juga menilai dengan berkesan keupayaan model bahasa besar (LLM), terutamanya keupayaan untuk memahami dan menaakul tentang pengetahuan saintifik. Walaupun pada masa ini terdapat banyak set data QA saintifik yang meliputi bidang perubatan, kimia, biologi dan bidang lain, set data ini masih mempunyai beberapa kekurangan. Pertama, borang data adalah agak mudah, kebanyakannya adalah soalan aneka pilihan. Ia mudah dinilai, tetapi mengehadkan julat pemilihan jawapan model dan tidak dapat menguji sepenuhnya keupayaan model untuk menjawab soalan saintifik. Sebaliknya, Soal Jawab terbuka
 Lima sekolah pembelajaran mesin yang anda tidak tahu
Jun 05, 2024 pm 08:51 PM
Lima sekolah pembelajaran mesin yang anda tidak tahu
Jun 05, 2024 pm 08:51 PM
Pembelajaran mesin ialah cabang penting kecerdasan buatan yang memberikan komputer keupayaan untuk belajar daripada data dan meningkatkan keupayaan mereka tanpa diprogramkan secara eksplisit. Pembelajaran mesin mempunyai pelbagai aplikasi dalam pelbagai bidang, daripada pengecaman imej dan pemprosesan bahasa semula jadi kepada sistem pengesyoran dan pengesanan penipuan, dan ia mengubah cara hidup kita. Terdapat banyak kaedah dan teori yang berbeza dalam bidang pembelajaran mesin, antaranya lima kaedah yang paling berpengaruh dipanggil "Lima Sekolah Pembelajaran Mesin". Lima sekolah utama ialah sekolah simbolik, sekolah sambungan, sekolah evolusi, sekolah Bayesian dan sekolah analogi. 1. Simbolisme, juga dikenali sebagai simbolisme, menekankan penggunaan simbol untuk penaakulan logik dan ekspresi pengetahuan. Aliran pemikiran ini percaya bahawa pembelajaran adalah proses penolakan terbalik, melalui sedia ada
 Prestasi SOTA, kaedah AI ramalan pertalian protein-ligan pelbagai mod Xiamen, menggabungkan maklumat permukaan molekul buat kali pertama
Jul 17, 2024 pm 06:37 PM
Prestasi SOTA, kaedah AI ramalan pertalian protein-ligan pelbagai mod Xiamen, menggabungkan maklumat permukaan molekul buat kali pertama
Jul 17, 2024 pm 06:37 PM
Editor |. KX Dalam bidang penyelidikan dan pembangunan ubat, meramalkan pertalian pengikatan protein dan ligan dengan tepat dan berkesan adalah penting untuk pemeriksaan dan pengoptimuman ubat. Walau bagaimanapun, kajian semasa tidak mengambil kira peranan penting maklumat permukaan molekul dalam interaksi protein-ligan. Berdasarkan ini, penyelidik dari Universiti Xiamen mencadangkan rangka kerja pengekstrakan ciri berbilang mod (MFE) novel, yang buat pertama kalinya menggabungkan maklumat mengenai permukaan protein, struktur dan jujukan 3D, dan menggunakan mekanisme perhatian silang untuk membandingkan ciri modaliti yang berbeza penjajaran. Keputusan eksperimen menunjukkan bahawa kaedah ini mencapai prestasi terkini dalam meramalkan pertalian mengikat protein-ligan. Tambahan pula, kajian ablasi menunjukkan keberkesanan dan keperluan maklumat permukaan protein dan penjajaran ciri multimodal dalam rangka kerja ini. Penyelidikan berkaitan bermula dengan "S
 Meletakkan pasaran seperti AI, GlobalFoundries memperoleh teknologi gallium nitrida Tagore Technology dan pasukan berkaitan
Jul 15, 2024 pm 12:21 PM
Meletakkan pasaran seperti AI, GlobalFoundries memperoleh teknologi gallium nitrida Tagore Technology dan pasukan berkaitan
Jul 15, 2024 pm 12:21 PM
Menurut berita dari laman web ini pada 5 Julai, GlobalFoundries mengeluarkan kenyataan akhbar pada 1 Julai tahun ini, mengumumkan pemerolehan teknologi power gallium nitride (GaN) Tagore Technology dan portfolio harta intelek, dengan harapan dapat mengembangkan bahagian pasarannya dalam kereta dan Internet of Things dan kawasan aplikasi pusat data kecerdasan buatan untuk meneroka kecekapan yang lebih tinggi dan prestasi yang lebih baik. Memandangkan teknologi seperti AI generatif terus berkembang dalam dunia digital, galium nitrida (GaN) telah menjadi penyelesaian utama untuk pengurusan kuasa yang mampan dan cekap, terutamanya dalam pusat data. Laman web ini memetik pengumuman rasmi bahawa semasa pengambilalihan ini, pasukan kejuruteraan Tagore Technology akan menyertai GLOBALFOUNDRIES untuk membangunkan lagi teknologi gallium nitride. G



