11 pengedaran asas yang saintis data menggunakan 95% masa
Mengikuti inventori terakhir "11 carta asas yang digunakan oleh saintis data 95% pada masanya", hari ini kami akan membawakan kepada anda 11 pengedaran asas yang digunakan oleh saintis data 95% pada masa itu. Menguasai pengedaran ini membantu kami memahami sifat data dengan lebih mendalam dan membuat inferens dan ramalan yang lebih tepat semasa analisis data dan membuat keputusan.

1. Taburan Normal
Taburan Normal, juga dikenali sebagai Taburan Gaussian, ialah taburan kebarangkalian berterusan. Ia mempunyai lengkung berbentuk loceng simetri dengan min (μ) sebagai pusat dan sisihan piawai (σ) sebagai lebar. Taburan normal mempunyai nilai aplikasi penting dalam banyak bidang seperti statistik, teori kebarangkalian, dan kejuruteraan.
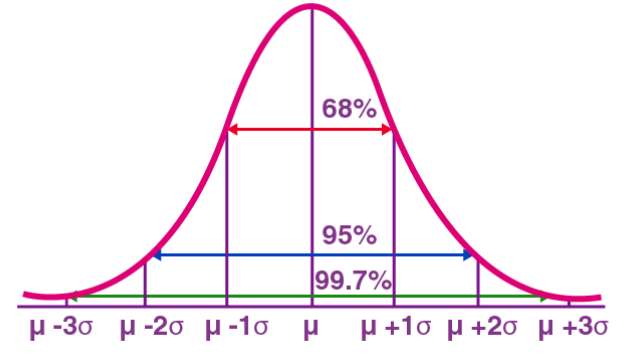
Fungsi ketumpatan kebarangkalian taburan normal boleh dinyatakan sebagai:
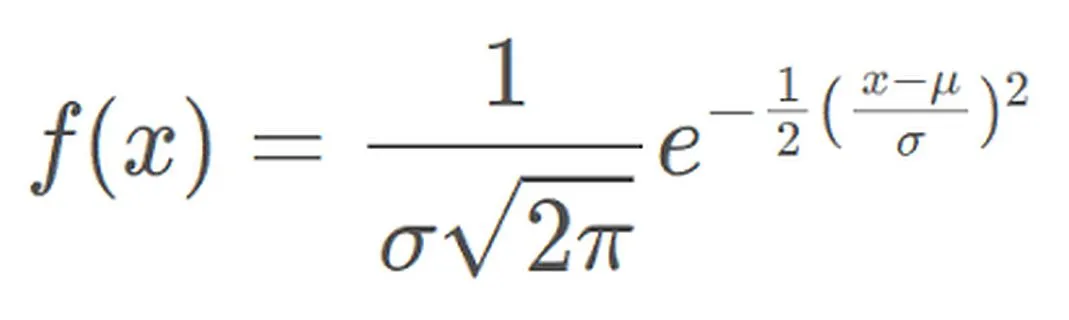
Fungsi ketumpatan kebarangkalian mewakili ketumpatan kebarangkalian nilai-nilai pembolehubah rawak teragih normal dalam selang unit berhampiran nilai yang diberikan x. Antaranya, μ mewakili min dan σ mewakili sisihan piawai Taburan normal digunakan secara meluas dalam amalan. Sebagai contoh, taburan ketinggian dan berat manusia menghampiri taburan normal. Tambahan pula, markah ujian selalunya diedarkan secara normal, dengan lebih sedikit orang yang mendapat markah tinggi dan rendah dan lebih ramai orang mendapat markah di tengah. Model pengedaran ini mempunyai nilai aplikasi yang penting dalam banyak bidang
2 Taburan Bernoulli
Taburan Bernoulli (Taburan Bernoulli) ialah taburan kebarangkalian diskret yang digunakan untuk menerangkan satu peristiwa dengan hanya dua kemungkinan hasil percubaan. Percubaan Bernoulli boleh menjadi kepala atau ekor, kejayaan atau kegagalan, ya atau tidak, dsb. Contohnya, membelek syiling, menguji sama ada produk itu layak, sama ada seseorang membeli produk tertentu, dsb.
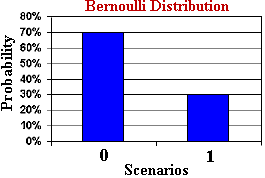 Fungsi jisim kebarangkalian bagi taburan Bernoulli ialah:
Fungsi jisim kebarangkalian bagi taburan Bernoulli ialah:
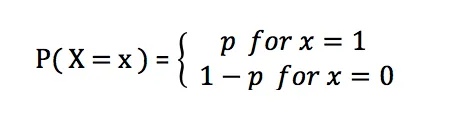 Dalam taburan Bernoulli, p mewakili kebarangkalian kejayaan, dan nilainya berjulat dari 0 hingga 1. Apabila p bersamaan 0.5, taburan Bernoulli menghampiri taburan seragam
Dalam taburan Bernoulli, p mewakili kebarangkalian kejayaan, dan nilainya berjulat dari 0 hingga 1. Apabila p bersamaan 0.5, taburan Bernoulli menghampiri taburan seragam
Aplikasi taburan Bernoulli dalam amalan: Contohnya, taburan binomial ialah n eksperimen berulang bebas bagi taburan Bernoulli.
3. Taburan binomial
Taburan binomial (Taburan Binomial) ialah taburan kebarangkalian diskret yang digunakan untuk menerangkan taburan kebarangkalian bilangan kejayaan dalam n eksperimen berulang bebas. Setiap percubaan hanya mempunyai dua kemungkinan hasil: kejayaan (dirakam sebagai 1) atau kegagalan (dirakam sebagai 0). Kebarangkalian kejayaan ialah p dan kebarangkalian kegagalan ialah 1-p.
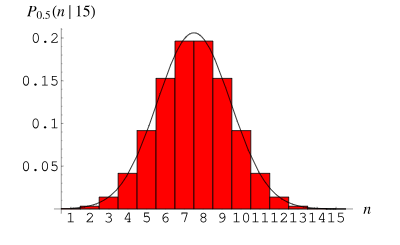 Fungsi jisim kebarangkalian taburan binomial boleh dinyatakan sebagai:
Fungsi jisim kebarangkalian taburan binomial boleh dinyatakan sebagai:
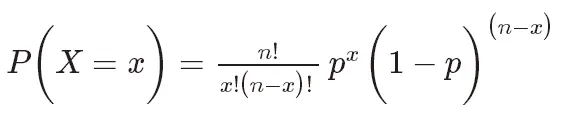 di mana, P(X=k) mewakili kebarangkalian k masa kejayaan,
di mana, P(X=k) mewakili kebarangkalian k masa kejayaan,
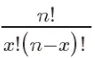 Pengagihan binomial digunakan secara meluas dalam amalan. Sebagai contoh, dalam penyelidikan perubatan, kita boleh menggunakan taburan binomial untuk mengira kadar kejayaan pesakit yang menerima rawatan tertentu. Dalam bidang kejuruteraan, kita boleh menggunakan taburan binomial untuk menilai kadar kelayakan sesuatu produk semasa proses pengeluaran. Ini adalah contoh penting taburan binomial dalam aplikasi praktikal
Pengagihan binomial digunakan secara meluas dalam amalan. Sebagai contoh, dalam penyelidikan perubatan, kita boleh menggunakan taburan binomial untuk mengira kadar kejayaan pesakit yang menerima rawatan tertentu. Dalam bidang kejuruteraan, kita boleh menggunakan taburan binomial untuk menilai kadar kelayakan sesuatu produk semasa proses pengeluaran. Ini adalah contoh penting taburan binomial dalam aplikasi praktikal
4. Taburan Poisson
Taburan Poisson (Taburan Poisson) ialah taburan kebarangkalian diskret yang digunakan untuk menerangkan bilangan peristiwa yang berlaku dalam tempoh masa yang tetap. Taburan Poisson sesuai untuk situasi di mana peristiwa adalah bebas dan berlaku pada kadar purata yang tetap.
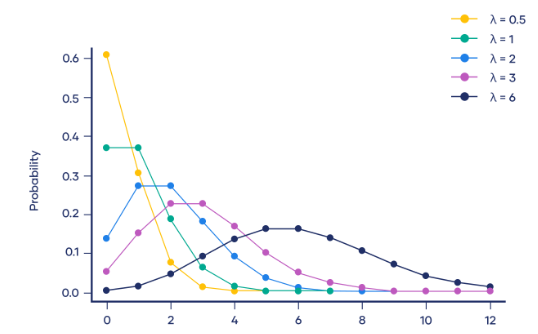 Fungsi ketumpatan kebarangkalian bagi taburan Poisson ialah:
Fungsi ketumpatan kebarangkalian bagi taburan Poisson ialah:
Di sini, P(X=k) mewakili kebarangkalian peristiwa berlaku k kali dalam tempoh masa yang tetap, dan λ mewakili kadar purata kejadian sesuatu peristiwa, iaitu purata bilangan peristiwa berlaku setiap unit masa. e ialah pemalar semula jadi, lebih kurang sama dengan 2.718. k mewakili bilangan peristiwa yang berlaku pengedaran Poisson digunakan secara meluas dalam amalan Sebagai contoh, dalam pusat panggilan, bilangan panggilan seminit boleh dianggap sebagai pengedaran Poisson, di mana purata bilangan panggilan seminit ialah λ
.5. Taburan eksponen
Taburan Eksponen (Taburan Eksponen) ialah taburan kebarangkalian berterusan yang digunakan untuk menerangkan kebarangkalian sesuatu peristiwa berlaku dalam masa yang ditetapkan. Taburan eksponen sesuai untuk situasi di mana peristiwa adalah bebas antara satu sama lain dan berlaku pada kadar purata yang tetap.
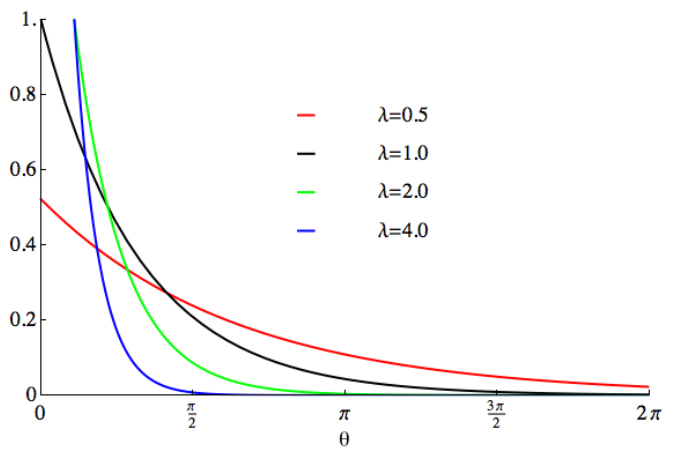 Fungsi ketumpatan kebarangkalian taburan eksponen ialah:
Fungsi ketumpatan kebarangkalian taburan eksponen ialah:
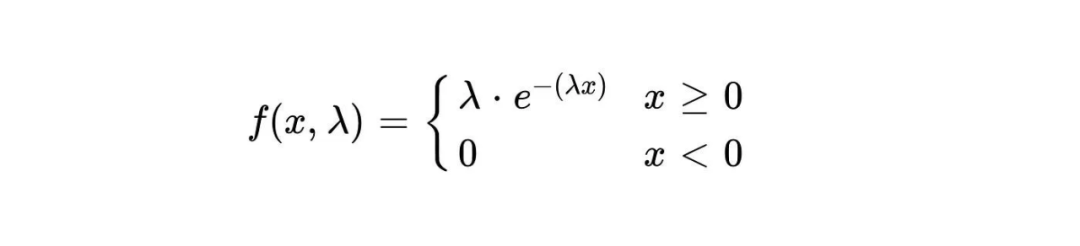 Ketumpatan kebarangkalian sesuatu kejadian yang berlaku dalam masa tertentu x diwakili oleh f(x,λ). λ mewakili purata kadar kejadian kejadian, iaitu purata bilangan kejadian yang berlaku setiap unit masa. e ialah pemalar semula jadi, lebih kurang sama dengan 2.718
Ketumpatan kebarangkalian sesuatu kejadian yang berlaku dalam masa tertentu x diwakili oleh f(x,λ). λ mewakili purata kadar kejadian kejadian, iaitu purata bilangan kejadian yang berlaku setiap unit masa. e ialah pemalar semula jadi, lebih kurang sama dengan 2.718
Taburan eksponen mempunyai banyak aplikasi dalam kehidupan sebenar. Contohnya, dalam pereputan radioaktif, masa pereputan nukleus radioaktif boleh dilihat sebagai taburan eksponen. Ini bermakna taburan kebarangkalian masa pereputan mengikut fungsi eksponen. Purata masa pereputan sepadan dengan parameter λ bagi fungsi eksponen
6 Taburan gamma
Taburan gamma ialah taburan kebarangkalian berterusan yang digunakan untuk menerangkan kebarangkalian sesuatu peristiwa berlaku dalam masa tertentu. Ia terpakai kepada situasi di mana peristiwa adalah bebas antara satu sama lain dan kadar kejadian purata sentiasa malar Fungsi ketumpatan kebarangkalian taburan gamma ialah:
 di mana f(x) mewakili masa x pada masa tertentu. ketumpatan kebarangkalian peristiwa dalaman. α dan β ialah parameter bentuk dan parameter kadar taburan gamma. α digunakan untuk menentukan bentuk taburan gamma, dan nilainya berjulat dari 0 hingga infiniti positif. β mewakili purata kadar kejadian kejadian, iaitu purata bilangan peristiwa yang berlaku setiap unit masa, dan julat nilai adalah dari 0 hingga infiniti positif. e ialah pemalar semula jadi, lebih kurang sama dengan 2.718 Aplikasi praktikal taburan gamma: Contohnya, pereputan radioaktif: Dalam pereputan radioaktif, masa untuk nukleus radioaktif untuk mereput boleh dianggap sebagai taburan gamma, dan masa pereputan purata ialah β/. α.
di mana f(x) mewakili masa x pada masa tertentu. ketumpatan kebarangkalian peristiwa dalaman. α dan β ialah parameter bentuk dan parameter kadar taburan gamma. α digunakan untuk menentukan bentuk taburan gamma, dan nilainya berjulat dari 0 hingga infiniti positif. β mewakili purata kadar kejadian kejadian, iaitu purata bilangan peristiwa yang berlaku setiap unit masa, dan julat nilai adalah dari 0 hingga infiniti positif. e ialah pemalar semula jadi, lebih kurang sama dengan 2.718 Aplikasi praktikal taburan gamma: Contohnya, pereputan radioaktif: Dalam pereputan radioaktif, masa untuk nukleus radioaktif untuk mereput boleh dianggap sebagai taburan gamma, dan masa pereputan purata ialah β/. α.
7. Taburan beta
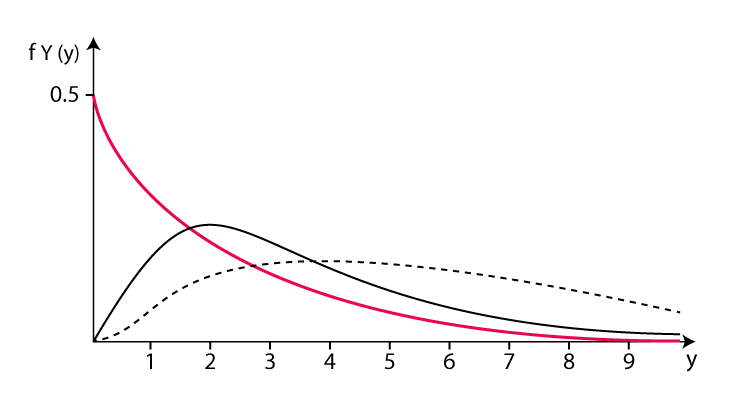
Taburan beta ialah taburan kebarangkalian berterusan yang digunakan untuk menerangkan taburan kebarangkalian bilangan kejayaan dalam satu set nilai. Ia mempunyai dua parameter, mewakili nilai jangkaan (min) dan sisihan piawai (sisihan piawai) kebarangkalian kejayaan. 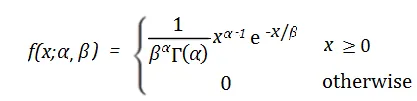
Fungsi ketumpatan kebarangkalian taburan beta adalah seperti berikut:
Dalam hal ini, x mewakili bilangan kejayaan, α dan β mewakili parameter bentuk taburan masing-masing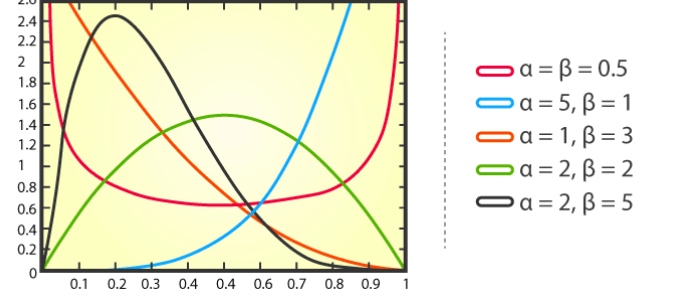 Taburan beta mempunyai aplikasi dalam banyak masalah praktikal. Sebagai contoh, dalam penyuntingan gen, penyelidik mungkin menggunakan pengedaran beta untuk meramalkan kebarangkalian bahawa teknologi penyuntingan gen akan berjaya mengedit tapak sasaran tertentu. Dalam bidang kewangan, pengedaran beta boleh digunakan untuk menerangkan turun naik harga aset, atau untuk mengira pulangan jangkaan portfolio pelaburan
Taburan beta mempunyai aplikasi dalam banyak masalah praktikal. Sebagai contoh, dalam penyuntingan gen, penyelidik mungkin menggunakan pengedaran beta untuk meramalkan kebarangkalian bahawa teknologi penyuntingan gen akan berjaya mengedit tapak sasaran tertentu. Dalam bidang kewangan, pengedaran beta boleh digunakan untuk menerangkan turun naik harga aset, atau untuk mengira pulangan jangkaan portfolio pelaburan
8 Pengagihan seragam
Pengagihan seragam ialah pengagihan kebarangkalian yang digunakan untuk menggambarkan set nilai dalam tertentu Teragih sama rata dalam selang waktu. Terdapat dua jenis taburan seragam: taburan seragam diskret dan taburan seragam berterusan. 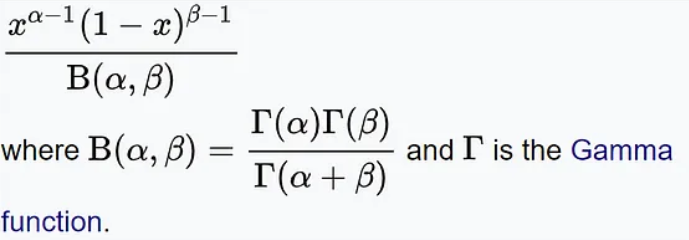
9. Taburan log-normal
Taburan log-normal (Taburan log-normal) ialah taburan kebarangkalian berterusan, yang dicirikan oleh logaritma pembolehubah rawak yang mematuhi taburan normal. Dalam erti kata lain, jika logaritma ln(X) pembolehubah rawak X mematuhi taburan normal, maka pembolehubah rawak X mematuhi taburan lognormal.
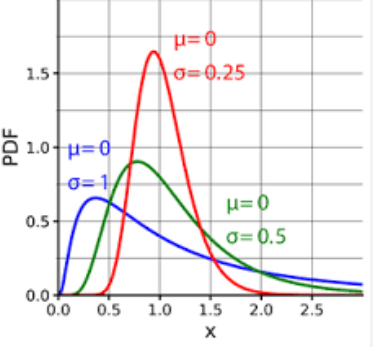
Fungsi ketumpatan kebarangkalian bagi taburan lognormal boleh dinyatakan sebagai:
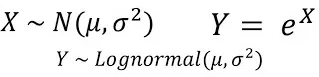
di mana μ ialah min bagi taburan lognormal dan σ ialah sisihan piawai bagi taburan lognormal.
Taburan lognormal sangat penting dalam banyak aplikasi praktikal, seperti kewangan (harga saham, hasil, dll.), biologi (kadar pertumbuhan, dll.), ekonomi (perbelanjaan pengguna, dll.), dll.
10. Taburan T Taburan
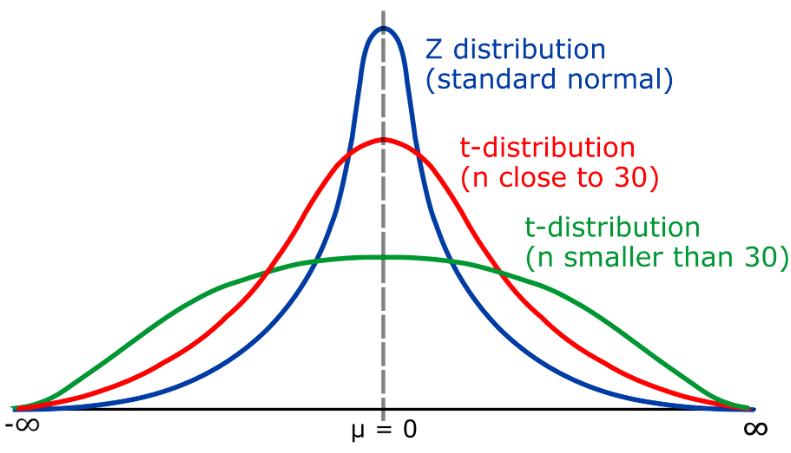
T ialah taburan kebarangkalian berterusan, terutamanya digunakan untuk menerangkan taburan min dalam kes sampel kecil. Taburan t adalah serupa dengan taburan normal, tetapi ekornya boleh memanjang ke kiri dan kanan, bergantung pada tahap kebebasan (k). Taburan-t digunakan secara meluas dalam inferens statistik, seperti dalam ujian hipotesis untuk menilai perbezaan ketara antara min sampel dan min populasi.
Jangkaan dan varians taburan t adalah seperti berikut:
E(t)=0
Kandungan yang akan ditulis semula ialah: Var(t)=k/(k-1)
darjah kebebasan taburan t ( k) mewakili hubungan antara saiz sampel (n) dan sisihan piawai populasi. Apabila k > 30, taburan t adalah hampir dengan taburan normal; apabila k hampir kepada 1, taburan t menjadi taburan Cauchy (Taburan Cauchy)
Dalam aplikasi praktikal, apabila saiz sampel besar (n>30) , ia boleh Gunakan taburan normal untuk melakukan ujian hipotesis Dalam kes ini, anda boleh menggunakan statistik z untuk mewujudkan selang keyakinan. Walau bagaimanapun, apabila saiz sampel adalah kecil (n
11. Taburan Weibull
Taburan Weibull (Taburan Weibull) ialah taburan kebarangkalian berterusan.
Fungsi ketumpatan kebarangkalian taburan Weibull ialah:
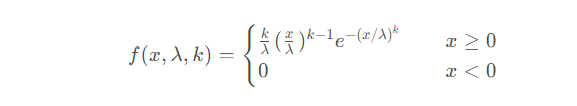
Dalam taburan Weibull, x dianggap sebagai pembolehubah rawak, λ dipanggil parameter skala (skala), dan k ialah parameter bentuk (bentuk). Setakat taburan Weber berkenaan, apabila k sama dengan 1, ia adalah taburan eksponen. Jika λ bersamaan dengan 1, ini ialah taburan Weber yang diminimumkan
Atas ialah kandungan terperinci 11 pengedaran asas yang saintis data menggunakan 95% masa. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

AI Hentai Generator
Menjana ai hentai secara percuma.

Artikel Panas

Alat panas

Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma

SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan

Hantar Studio 13.0.1
Persekitaran pembangunan bersepadu PHP yang berkuasa

Dreamweaver CS6
Alat pembangunan web visual

SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)

Topik panas
 1374
1374
 52
52
 Baca fail CSV dan lakukan analisis data menggunakan panda
Jan 09, 2024 am 09:26 AM
Baca fail CSV dan lakukan analisis data menggunakan panda
Jan 09, 2024 am 09:26 AM
Pandas ialah alat analisis data yang berkuasa yang boleh membaca dan memproses pelbagai jenis fail data dengan mudah. Antaranya, fail CSV ialah salah satu daripada format fail data yang paling biasa dan biasa digunakan. Artikel ini akan memperkenalkan cara menggunakan Panda untuk membaca fail CSV dan melakukan analisis data serta memberikan contoh kod khusus. 1. Import perpustakaan yang diperlukan Mula-mula, kita perlu mengimport perpustakaan Pandas dan perpustakaan lain yang berkaitan yang mungkin diperlukan, seperti yang ditunjukkan di bawah: importpandasaspd 2. Baca fail CSV menggunakan Pan
 Pengenalan kepada kaedah analisis data
Jan 08, 2024 am 10:22 AM
Pengenalan kepada kaedah analisis data
Jan 08, 2024 am 10:22 AM
Kaedah analisis data biasa: 1. Kaedah analisis perbandingan 3. Kaedah analisis silang 5. Kaedah analisis sebab dan akibat , Kaedah analisis komponen utama 9. Kaedah analisis serakan 10. Kaedah analisis matriks. Pengenalan terperinci: 1. Kaedah analisis perbandingan: Analisis perbandingan dua atau lebih data untuk mencari perbezaan dan corak 2. Kaedah analisis struktur: Kaedah analisis perbandingan antara setiap bahagian keseluruhan dan keseluruhan; , dsb.
 11 pengedaran asas yang saintis data menggunakan 95% masa
Dec 15, 2023 am 08:21 AM
11 pengedaran asas yang saintis data menggunakan 95% masa
Dec 15, 2023 am 08:21 AM
Berikutan inventori terakhir "11 Saintis Data Carta Asas Menggunakan 95% Masa", hari ini kami akan membawakan kepada anda 11 pengedaran asas yang digunakan oleh saintis data 95% daripada masa. Menguasai pengedaran ini membantu kami memahami sifat data dengan lebih mendalam dan membuat inferens dan ramalan yang lebih tepat semasa analisis data dan membuat keputusan. 1. Taburan Normal Taburan Normal, juga dikenali sebagai Taburan Gaussian, ialah taburan kebarangkalian berterusan. Ia mempunyai lengkung berbentuk loceng simetri dengan min (μ) sebagai pusat dan sisihan piawai (σ) sebagai lebar. Taburan normal mempunyai nilai aplikasi penting dalam banyak bidang seperti statistik, teori kebarangkalian, dan kejuruteraan.
 Pembelajaran mesin dan analisis data menggunakan bahasa Go
Nov 30, 2023 am 08:44 AM
Pembelajaran mesin dan analisis data menggunakan bahasa Go
Nov 30, 2023 am 08:44 AM
Dalam masyarakat pintar hari ini, pembelajaran mesin dan analisis data merupakan alat yang sangat diperlukan yang boleh membantu orang ramai memahami dan menggunakan sejumlah besar data dengan lebih baik. Dalam bidang ini, bahasa Go juga telah menjadi bahasa pengaturcaraan yang telah menarik perhatian ramai. Artikel ini memperkenalkan cara menggunakan bahasa Go untuk pembelajaran mesin dan analisis data. 1. Ekosistem pembelajaran mesin bahasa Go tidak sekaya Python dan R. Walau bagaimanapun, apabila semakin ramai orang mula menggunakannya, beberapa perpustakaan dan rangka kerja pembelajaran mesin
 11 Visualisasi Lanjutan untuk Analisis Data dan Pembelajaran Mesin
Oct 25, 2023 am 08:13 AM
11 Visualisasi Lanjutan untuk Analisis Data dan Pembelajaran Mesin
Oct 25, 2023 am 08:13 AM
Visualisasi ialah alat yang berkuasa untuk menyampaikan corak dan hubungan data yang kompleks dengan cara yang intuitif dan mudah difahami. Mereka memainkan peranan penting dalam analisis data, memberikan cerapan yang selalunya sukar untuk dibezakan daripada data mentah atau perwakilan berangka tradisional. Visualisasi adalah penting untuk memahami corak dan perhubungan data yang kompleks, dan kami akan memperkenalkan 11 carta paling penting dan mesti diketahui yang membantu mendedahkan maklumat dalam data dan menjadikan data kompleks lebih mudah difahami dan bermakna. 1. KSPlotKSPlot digunakan untuk menilai perbezaan taburan. Idea teras adalah untuk mengukur jarak maksimum antara fungsi pengedaran kumulatif (CDF) dua pengedaran. Semakin kecil jarak maksimum, semakin besar kemungkinan mereka tergolong dalam pengedaran yang sama. Oleh itu, ia terutamanya ditafsirkan sebagai "sistem" untuk menentukan perbezaan pengedaran.
 Cara menggunakan antara muka ECharts dan php untuk melaksanakan analisis data dan ramalan carta statistik
Dec 17, 2023 am 10:26 AM
Cara menggunakan antara muka ECharts dan php untuk melaksanakan analisis data dan ramalan carta statistik
Dec 17, 2023 am 10:26 AM
Cara menggunakan antara muka ECharts dan PHP untuk melaksanakan analisis data dan ramalan carta statistik Analisis dan ramalan data memainkan peranan penting dalam pelbagai bidang. Ia boleh membantu kami memahami arah aliran dan corak data dan menyediakan rujukan untuk keputusan masa hadapan. ECharts ialah perpustakaan visualisasi data sumber terbuka yang menyediakan komponen carta yang kaya dan fleksibel yang boleh memuatkan dan memproses data secara dinamik dengan menggunakan antara muka PHP. Artikel ini akan memperkenalkan kaedah pelaksanaan analisis data carta statistik dan ramalan berdasarkan ECharts dan antara muka php, dan menyediakan
 Perjalanan romantik Python dan pembelajaran mesin, satu langkah daripada orang baru kepada pakar
Feb 23, 2024 pm 08:34 PM
Perjalanan romantik Python dan pembelajaran mesin, satu langkah daripada orang baru kepada pakar
Feb 23, 2024 pm 08:34 PM
1. Pertemuan antara Python dan pembelajaran mesin Sebagai bahasa pengaturcaraan yang mudah dipelajari dan berkuasa, Python sangat disukai oleh pembangun. Pembelajaran mesin, sebagai cabang kecerdasan buatan, bertujuan untuk membolehkan komputer belajar cara belajar daripada data dan membuat ramalan atau keputusan. Gabungan Python dan pembelajaran mesin adalah padanan yang sempurna, membawakan kami satu siri alatan dan perpustakaan yang berkuasa, menjadikan pembelajaran mesin lebih mudah untuk dilaksanakan dan diterapkan. 2. Meneroka Perpustakaan Pembelajaran Mesin Python Python menyediakan banyak perpustakaan pembelajaran mesin yang kaya dengan ciri, yang paling popular termasuk: NumPy: menyediakan fungsi pengiraan berangka yang cekap dan merupakan perpustakaan asas untuk pembelajaran mesin. SciPy: Menyediakan alat pengkomputeran saintifik yang lebih maju, adalah
 Analisis data Excel bersepadu
Mar 21, 2024 am 08:21 AM
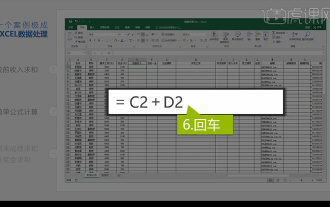
Analisis data Excel bersepadu
Mar 21, 2024 am 08:21 AM
1. Dalam pelajaran ini, kami akan menerangkan analisis data Excel bersepadu Kami akan melengkapkannya melalui kes Buka bahan kursus dan klik pada sel E2 untuk memasukkan formula. 2. Kami kemudian memilih sel E53 untuk mengira semua data berikut. 3. Kemudian kita klik pada sel F2, dan kemudian kita masukkan formula untuk mengiranya Begitu juga, menyeret ke bawah boleh mengira nilai yang kita mahu. 4. Kami memilih sel G2, klik tab Data, klik Pengesahan Data, pilih dan sahkan. 5. Mari kita gunakan kaedah yang sama untuk mengisi secara automatik sel di bawah yang perlu dikira. 6. Seterusnya, kami mengira gaji sebenar dan pilih sel H2 untuk memasukkan formula. 7. Kemudian kita klik pada menu drop-down nilai untuk klik pada nombor lain.




