 Peranti teknologi
Peranti teknologi
 AI
AI
 Lebih 70% mAP buat kali pertama! GeMap: Peta berketepatan tinggi tempatan SOTA dimuat semula
Lebih 70% mAP buat kali pertama! GeMap: Peta berketepatan tinggi tempatan SOTA dimuat semula
Lebih 70% mAP buat kali pertama! GeMap: Peta berketepatan tinggi tempatan SOTA dimuat semula
Ditulis di atas & pemahaman peribadi pengarang
Membina peta berketepatan tinggi bervektor berdasarkan data penderia dalam masa nyata adalah penting untuk tugas hiliran seperti ramalan dan perancangan, dan boleh mengimbangi prestasi masa nyata luar talian yang lemah dengan berkesan peta berketepatan tinggi. Dengan pembangunan pembelajaran mendalam, pembinaan peta berketepatan tinggi bervektor dalam talian telah muncul secara beransur-ansur, dan karya perwakilan seperti HDMapNet dan MapTR telah muncul satu demi satu. Walau bagaimanapun, kaedah pembinaan peta berketepatan tinggi vektor sedia ada tidak mempunyai penerokaan sifat geometri unsur peta (termasuk bentuk unsur, menegak, selari dan perhubungan geometri lain).
Sifat geometri peta berketepatan tinggi tervektor
Peta berketepatan tinggi bervektor sangat mengabstraksi elemen di jalan dan mewakili setiap elemen peta sebagai jujukan titik dua dimensi. Reka bentuk jalan bandar mempunyai spesifikasi khusus Contohnya, dalam kebanyakan kes, laluan pejalan kaki adalah segi empat sama segi empat tepat atau paralelogram; Elemen yang berbeza dalam peta definisi tinggi juga mempunyai banyak ciri yang serupa Peraturan akal sehat ini disarikan ke dalam sifat geometri peta berketepatan tinggi, termasuk bentuk elemen peta (segi empat tepat, selari, garis lurus, dsb. ), atau peta yang berbeza Hubungan antara elemen (selari, menegak, dll.). Sifat geometri sangat mengekang perwakilan unsur peta Jika anda memahami sepenuhnya sifat geometri pembinaan model dalam talian, anda boleh mendapatkan hasil yang lebih tepat.
Cadangkan kepentingan perwakilan geometri untuk peta berketepatan tinggiWalaupun secara teori masih mungkin bagi model sedia ada untuk mempelajari sifat geometri unsur peta, namun ciri ciri geometri menentukan bahawa, sekurang-kurangnya di bawah kaedah tradisional. reka bentuk, model tidak Tidak mudah untuk belajar.
- Invarian sifat geometri
- Apabila kenderaan tengah memandu terus di jalan raya, menukar lorong atau membelok,
elemen peta (dalam sistem koordinat kenderaan) terus berubah. Bentuk pejalan kaki, lorong, sempadan jalan, dan lain-lain tidak akan berubah sama, hubungan selari antara lorong tidak akan berubah. Sifat geometri unsur peta adalah objektif, dan salah satu ciri pentingnya ialah invarian. Lebih khusus lagi, ia ialah invarian tegar (kekal invarian kepada putaran dan transformasi terjemahan). Kerja sebelumnya, sama ada menggunakan perwakilan poligaris mudah atau menggunakan lengkung polinomial dengan titik kawalan (seperti lengkung Bezier, lengkung Bezier sekeping), semuanya berdasarkan koordinat mutlak dan hujung ke hujung berdasarkan pengoptimuman koordinat mutlak. Objektif pengoptimuman berdasarkan koordinat mutlak itu sendiri tidak mempunyai invarian tegar, jadi sukar untuk menjangkakan bahawa penyelesaian optimum tempatan yang model jatuh ke dalamnya mengandungi pemahaman tentang sifat geometri. Oleh itu, perwakilan yang boleh mencirikan sepenuhnya sifat geometri dan mempunyai invarian tertentu adalah perlu.
Rajah 1. Contoh invarian geometri. Apabila kenderaan membelok ke kanan, koordinat mutlak akan berubah dengan ketara. Imej di sebelah kanan menunjukkan senario kehidupan sebenar yang sepadan.
Apabila kenderaan membelok ke kanan, koordinat mutlak akan berubah dengan ketara. Imej di sebelah kanan menunjukkan senario kehidupan sebenar yang sepadan.
- Kepelbagaian sifat geometri
- Tambahan pula, walaupun pengetahuan terdahulu yang kukuh, sifat geometri jalan masih pelbagai. Pelbagai sifat geometri ini secara amnya boleh dibahagikan kepada dua kategori, satu adalah mengenai bentuk geometri elemen peta tunggal, dan satu lagi adalah mengenai persatuan geometri unsur peta yang berbeza. Disebabkan oleh kepelbagaian sifat geometri, adalah mustahil untuk menukar sifat geometri secara menyeluruh dan manual kepada kekangan, jadi kami lebih suka model itu boleh belajar secara autonomi pelbagai sifat geometri dari hujung ke hujung.
Reka bentuk GeMap
Perwakilan geometriMemandangkan dua masalah di atas, kami terlebih dahulu menambah baik kaedah perwakilan. Kami berharap dapat memperkenalkan perwakilan geometri yang baik sebagai tambahan kepada perwakilan berasaskan koordinat mutlak tradisional, yang perlu memenuhi keperluan berikut:
boleh menggambarkan bentuk elemen peta
boleh menggambarkan- perkaitan
- antara elemen peta Ketegaran invarian
- Untuk memastikan
- terjemahan invarian , kami menggunakan kuantiti relatif, iaitu, vektor mengimbangi antara titik untuk memastikan lagi invarian putaran , kami memilih panjang
sudut antara vektor offset yang berbeza. Kedua-dua ini - panjang dan sudut - membentuk asas perwakilan geometri yang kami cadangkan. Di samping itu, untuk membezakan dan menerangkan bentuk dengan lebih baik dan mengaitkan dua jenis sifat geometri yang berbeza, kami memperhalusi reka bentuk mengikut prinsip kesederhanaan: Untuk menerangkan bentuk, kami mengira jarak antara titik bersebelahan dalam elemen peta tunggal mengimbangi vektor di antara mereka, dan mengira panjang vektor mengimbangi dan sudut antara vektor mengimbangi bersebelahan. Perwakilan ini secara unik mengenal pasti mana-mana polyline/poligon. Contoh dua imej ditunjukkan di bawah:
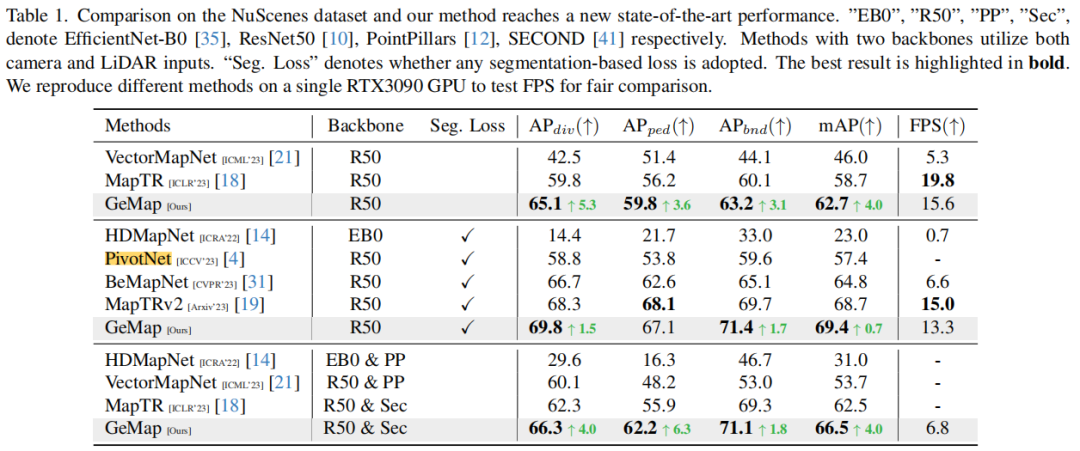
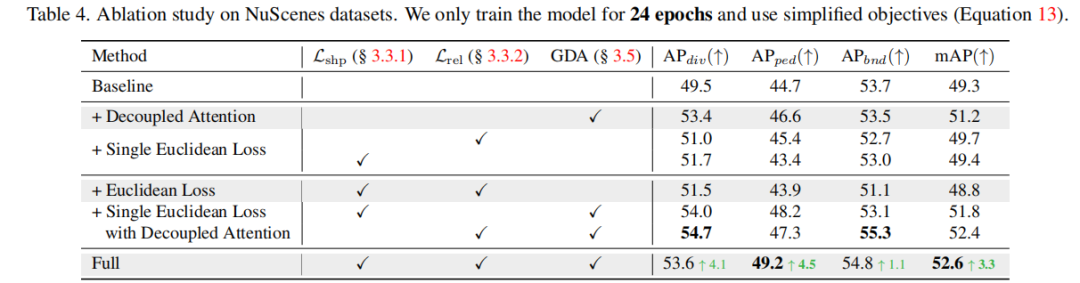
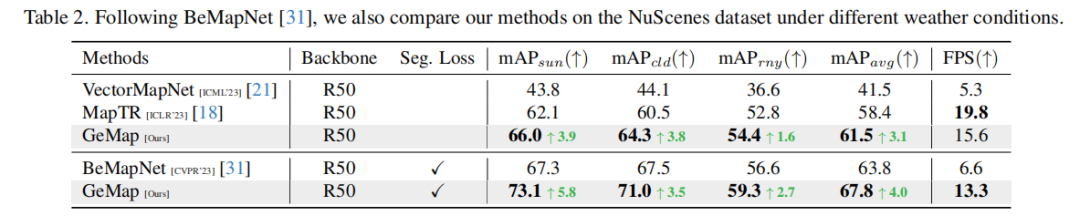
Sila lihat Rajah 2, yang menunjukkan perwakilan bentuk geometri Untuk segi empat tepat, ia boleh diterangkan dengan menggunakan sudut tepat dan dua pasang sisi yang sama untuk garis lurus, semua sudut yang disertakan ialah 0 darjah atau 180 darjah . Untuk mencirikan persatuan, begitu juga, kita mula-mula mempertimbangkan jarak antara mana-mana dua titik. Walau bagaimanapun, jika sudut dikira untuk semua vektor offset titik ke titik, kerumitan perwakilan adalah terlalu tinggi dan kos pengiraan tidak mampu dibeli. Secara khusus, dengan mengandaikan bahawa terdapat sejumlah elemen peta, dan setiap elemen diwakili oleh satu titik, jumlah data untuk semua sudut akan mencapai (apabila mengambil 1000, dengan mengandaikan bahawa setiap data sudut ialah nombor titik terapung 32-bit, seperti perwakilan hanya Ruang yang diduduki akan mencapai tahap TB). Sebenarnya, ini tidak diperlukan untuk perhubungan menegak, selari, dsb. biasa. Oleh itu, kita mula-mula mengira offset di dalam elemen, dan kemudian hanya mengira sudut antara setiap pasangan ofset ini sebagai sebahagian daripada perwakilan geometri. Perwakilan perkaitan yang dipermudahkan ini mengekalkan keupayaan untuk menerangkan perhubungan selari, menegak dan lain-lain, manakala volum data yang sepadan adalah sahaja (kira-kira 4MB di bawah keadaan yang dinyatakan di atas). Untuk memudahkan pemahaman, kami juga menyediakan beberapa contoh: Rajah 3. Perwakilan persatuan geometri. Hubungan selari dan hubungan serenjang dinyatakan dengan sudut antara vektor offset ialah 0 darjah atau 90 darjah; jarak antara dua titik boleh mencerminkan maklumat lebar lorong pada tahap tertentu bentuk dan perkaitan geometri yang dioptimumkan, kami menggunakan pendekatan yang paling mudah, : . Ini bermakna meninggalkan persepsi bentuk dan perkaitan boleh membawa kepada hasil yang lebih baik. Untuk memisahkan pemprosesan geometri dan perkaitan, kami menggunakan dua langkah perhatian kendiri: Setiap elemen peta termasuk pertanyaan, dan perhatian dilakukan di dalam Hasil eksperimen Kami menjalankan sejumlah besar eksperimen pada set data nuScenes dan Argoverse 2. Kedua-duanya adalah set data pemanduan autonomi berskala besar yang biasa digunakan, dan kedua-duanya menyediakan anotasi peta. Kami menjalankan tiga set eksperimen pada nuScenes. Pertama, kami menggunakan gabungan fungsi objektif yang agak tulen, termasuk hanya kerugian geometri dan kerugian lain yang diperlukan (seperti jarak titik ke titik, arah tepi, klasifikasi Gabungan ini bertujuan untuk menyerlahkan kepentingan sifat geometri yang kami cadangkan). nilai tanpa terlalu mengejar keputusan SOTA. Keputusan menunjukkan bahawa kaedah kami meningkatkan mAP berbanding dengan MapTR dalam kes ini. Untuk meneroka had GeMap, kami juga menambah beberapa objektif tambahan, termasuk pembahagian dan anggaran kedalaman. Dalam kes ini, kami juga mencapai keputusan SOTA (peningkatan mAP). Perlu diingat bahawa untuk mencapai peningkatan sedemikian tidak memerlukan pengorbanan terlalu banyak kelajuan inferens. Akhir sekali, kami juga cuba memperkenalkan input modal LiDAR tambahan Dengan bantuan input modal tambahan, prestasi GeMap telah dipertingkatkan lagi Begitu juga, pada set data Argoverse 2, kaedah kami juga mencapai kesan hasil yang sangat cemerlang. Kandungan yang ditulis semula ialah: eksperimen ablasi Kandungan yang ditulis semula selanjutnya pada nuScenes ialah: eksperimen ablasi membuktikan nilai kehilangan geometri dan perhatian yang dipisahkan secara geometri. Menariknya, seperti yang kami jangkakan, menggunakan kehilangan geometri secara langsung akan membawa kepada penurunan dalam prestasi model. Kami percaya ini adalah kerana gandingan struktur pemprosesan bentuk dan perkaitan menyukarkan model untuk mengoptimumkan perwakilan geometri dan selepas digabungkan dengan perhatian penyahgandingan geometri, kehilangan geometri memainkan peranannya (daripada "+ Euclidean Loss" hingga; "Penuh"). Lebih banyak hasil 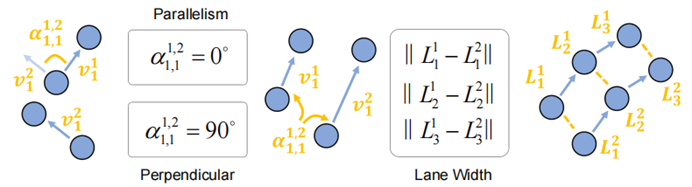
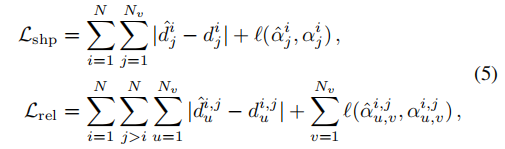 di mana dan mewakili panjang dan sudut yang dikira berdasarkan label, masing-masing, dan jumlah mewakili Ramalkan panjang dan sudut yang dikira. Helah digunakan apabila menangani sudut yang disertakan: pengiraan sudut secara langsung melibatkan fungsi arctan terputus, yang akan menghadapi kesukaran semasa pengoptimuman (terdapat masalah kecerunan yang lenyap berhampiran ±90 darjah), jadi perkara yang sebenarnya kita bandingkan ialah sudut yang disertakan Kosinus dan sinus Kekukuhan
di mana dan mewakili panjang dan sudut yang dikira berdasarkan label, masing-masing, dan jumlah mewakili Ramalkan panjang dan sudut yang dikira. Helah digunakan apabila menangani sudut yang disertakan: pengiraan sudut secara langsung melibatkan fungsi arctan terputus, yang akan menghadapi kesukaran semasa pengoptimuman (terdapat masalah kecerunan yang lenyap berhampiran ±90 darjah), jadi perkara yang sebenarnya kita bandingkan ialah sudut yang disertakan Kosinus dan sinus Kekukuhan 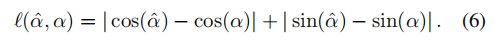
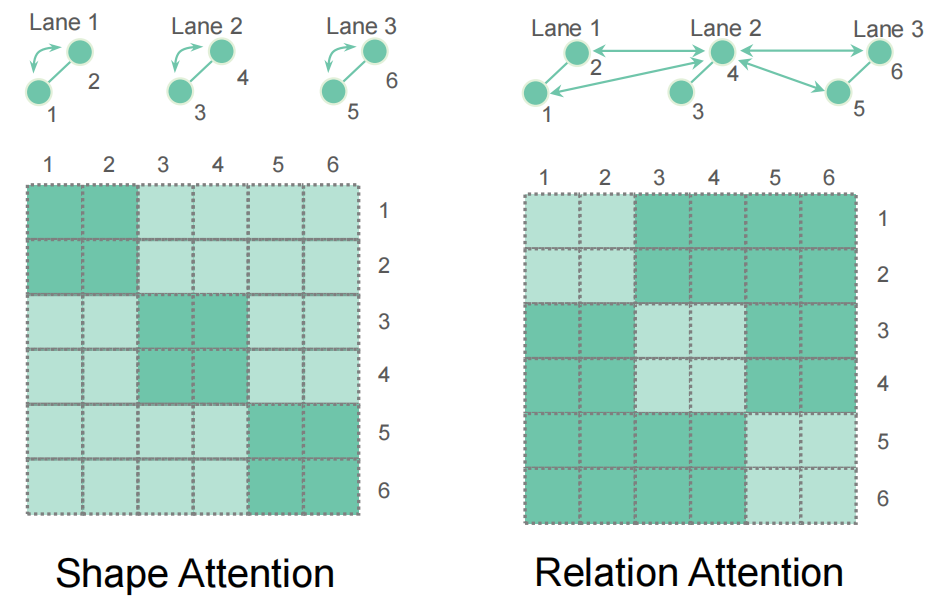
Sebelah kiri ialah perhatian bentuk yang dilakukan dalam satu elemen, dan sebelah kanan ialah perhatian berkaitan yang dilakukan antara elemen.

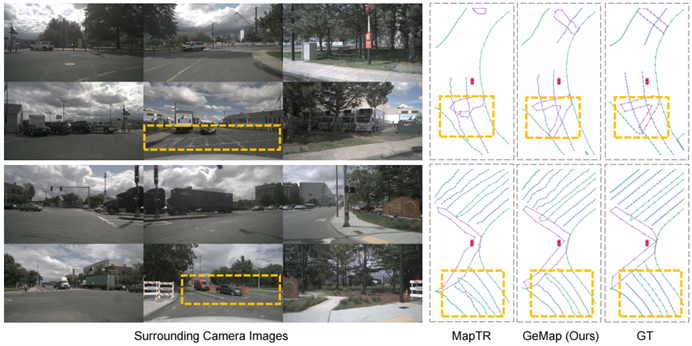
Ringkasan
Kami menunjukkan sifat geometri unsur peta dan nilainya untuk pembinaan peta berketepatan tinggi dalam talian . Berdasarkan ini, kami mencadangkan kaedah yang berkuasa untuk mengesahkan nilai ini pada mulanya. Selain itu, keteguhan GeMap terhadap oklusi mungkin menunjukkan idea menggunakan sifat geometri untuk menangani oklusi dalam tugas pemanduan autonomi lain (seperti pengesanan, ramalan penghunian, dll.) - kerana kedua-dua kenderaan dan jalan mempunyai sifat geometri yang agak piawai. Sudah tentu, kaedah kami sendiri mempunyai banyak perkara untuk diterokai dengan lebih lanjut. Sebagai contoh, bolehkah unsur-unsur geometri dengan kerumitan yang berbeza digambarkan secara adaptif menggunakan titik yang berbeza? Adakah mungkin untuk memahami perwakilan geometri dari perspektif kebarangkalian dan menjadikannya lebih mantap kepada bunyi? Kerana kita telah memudahkan perkaitan unsur, adakah terdapat perwakilan perkaitan geometri yang lebih baik? Ini semua arahan untuk pengoptimuman selanjutnya.

Atas ialah kandungan terperinci Lebih 70% mAP buat kali pertama! GeMap: Peta berketepatan tinggi tempatan SOTA dimuat semula. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

AI Hentai Generator
Menjana ai hentai secara percuma.

Artikel Panas

Alat panas

Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma

SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan

Hantar Studio 13.0.1
Persekitaran pembangunan bersepadu PHP yang berkuasa

Dreamweaver CS6
Alat pembangunan web visual

SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)

Topik panas
 1376
1376
 52
52
 Bagaimana untuk menjadikan Peta Google sebagai peta lalai dalam iPhone
Apr 17, 2024 pm 07:34 PM
Bagaimana untuk menjadikan Peta Google sebagai peta lalai dalam iPhone
Apr 17, 2024 pm 07:34 PM
Peta lalai pada iPhone ialah Peta, pembekal geolokasi proprietari Apple. Walaupun peta semakin baik, ia tidak berfungsi dengan baik di luar Amerika Syarikat. Ia tiada apa-apa untuk ditawarkan berbanding Peta Google. Dalam artikel ini, kami membincangkan langkah yang boleh dilaksanakan untuk menggunakan Peta Google untuk menjadi peta lalai pada iPhone anda. Cara Menjadikan Peta Google Peta Lalai dalam iPhone Menetapkan Peta Google sebagai aplikasi peta lalai pada telefon anda adalah lebih mudah daripada yang anda fikirkan. Ikut langkah di bawah – Langkah prasyarat – Anda mesti memasang Gmail pada telefon anda. Langkah 1 – Buka AppStore. Langkah 2 – Cari “Gmail”. Langkah 3 – Klik di sebelah apl Gmail
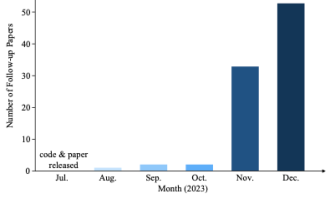 Mengapakah Gaussian Splatting begitu popular dalam pemanduan autonomi sehingga NeRF mula ditinggalkan?
Jan 17, 2024 pm 02:57 PM
Mengapakah Gaussian Splatting begitu popular dalam pemanduan autonomi sehingga NeRF mula ditinggalkan?
Jan 17, 2024 pm 02:57 PM
Ditulis di atas & pemahaman peribadi pengarang Gaussiansplatting tiga dimensi (3DGS) ialah teknologi transformatif yang telah muncul dalam bidang medan sinaran eksplisit dan grafik komputer dalam beberapa tahun kebelakangan ini. Kaedah inovatif ini dicirikan oleh penggunaan berjuta-juta Gaussians 3D, yang sangat berbeza daripada kaedah medan sinaran saraf (NeRF), yang terutamanya menggunakan model berasaskan koordinat tersirat untuk memetakan koordinat spatial kepada nilai piksel. Dengan perwakilan adegan yang eksplisit dan algoritma pemaparan yang boleh dibezakan, 3DGS bukan sahaja menjamin keupayaan pemaparan masa nyata, tetapi juga memperkenalkan tahap kawalan dan pengeditan adegan yang tidak pernah berlaku sebelum ini. Ini meletakkan 3DGS sebagai penukar permainan yang berpotensi untuk pembinaan semula dan perwakilan 3D generasi akan datang. Untuk tujuan ini, kami menyediakan gambaran keseluruhan sistematik tentang perkembangan dan kebimbangan terkini dalam bidang 3DGS buat kali pertama.
 Bagaimana untuk menyelesaikan masalah ekor panjang dalam senario pemanduan autonomi?
Jun 02, 2024 pm 02:44 PM
Bagaimana untuk menyelesaikan masalah ekor panjang dalam senario pemanduan autonomi?
Jun 02, 2024 pm 02:44 PM
Semalam semasa temu bual, saya telah ditanya sama ada saya telah membuat sebarang soalan berkaitan ekor panjang, jadi saya fikir saya akan memberikan ringkasan ringkas. Masalah ekor panjang pemanduan autonomi merujuk kepada kes tepi dalam kenderaan autonomi, iaitu, kemungkinan senario dengan kebarangkalian yang rendah untuk berlaku. Masalah ekor panjang yang dirasakan adalah salah satu sebab utama yang kini mengehadkan domain reka bentuk pengendalian kenderaan autonomi pintar satu kenderaan. Seni bina asas dan kebanyakan isu teknikal pemanduan autonomi telah diselesaikan, dan baki 5% masalah ekor panjang secara beransur-ansur menjadi kunci untuk menyekat pembangunan pemanduan autonomi. Masalah ini termasuk pelbagai senario yang berpecah-belah, situasi yang melampau dan tingkah laku manusia yang tidak dapat diramalkan. "Ekor panjang" senario tepi dalam pemanduan autonomi merujuk kepada kes tepi dalam kenderaan autonomi (AVs) kes Edge adalah senario yang mungkin dengan kebarangkalian yang rendah untuk berlaku. kejadian yang jarang berlaku ini
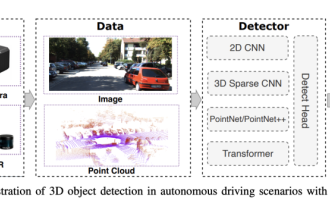 Pilih kamera atau lidar? Kajian terbaru tentang mencapai pengesanan objek 3D yang mantap
Jan 26, 2024 am 11:18 AM
Pilih kamera atau lidar? Kajian terbaru tentang mencapai pengesanan objek 3D yang mantap
Jan 26, 2024 am 11:18 AM
0. Ditulis di hadapan&& Pemahaman peribadi bahawa sistem pemanduan autonomi bergantung pada persepsi lanjutan, membuat keputusan dan teknologi kawalan, dengan menggunakan pelbagai penderia (seperti kamera, lidar, radar, dll.) untuk melihat persekitaran sekeliling dan menggunakan algoritma dan model untuk analisis masa nyata dan membuat keputusan. Ini membolehkan kenderaan mengenali papan tanda jalan, mengesan dan menjejaki kenderaan lain, meramalkan tingkah laku pejalan kaki, dsb., dengan itu selamat beroperasi dan menyesuaikan diri dengan persekitaran trafik yang kompleks. Teknologi ini kini menarik perhatian meluas dan dianggap sebagai kawasan pembangunan penting dalam pengangkutan masa depan satu. Tetapi apa yang menyukarkan pemanduan autonomi ialah memikirkan cara membuat kereta itu memahami perkara yang berlaku di sekelilingnya. Ini memerlukan algoritma pengesanan objek tiga dimensi dalam sistem pemanduan autonomi boleh melihat dan menerangkan dengan tepat objek dalam persekitaran sekeliling, termasuk lokasinya,
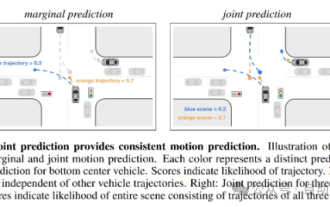 Artikel ini sudah cukup untuk anda membaca tentang pemanduan autonomi dan ramalan trajektori!
Feb 28, 2024 pm 07:20 PM
Artikel ini sudah cukup untuk anda membaca tentang pemanduan autonomi dan ramalan trajektori!
Feb 28, 2024 pm 07:20 PM
Ramalan trajektori memainkan peranan penting dalam pemanduan autonomi Ramalan trajektori pemanduan autonomi merujuk kepada meramalkan trajektori pemanduan masa hadapan kenderaan dengan menganalisis pelbagai data semasa proses pemanduan kenderaan. Sebagai modul teras pemanduan autonomi, kualiti ramalan trajektori adalah penting untuk kawalan perancangan hiliran. Tugas ramalan trajektori mempunyai timbunan teknologi yang kaya dan memerlukan kebiasaan dengan persepsi dinamik/statik pemanduan autonomi, peta ketepatan tinggi, garisan lorong, kemahiran seni bina rangkaian saraf (CNN&GNN&Transformer), dll. Sangat sukar untuk bermula! Ramai peminat berharap untuk memulakan ramalan trajektori secepat mungkin dan mengelakkan perangkap Hari ini saya akan mengambil kira beberapa masalah biasa dan kaedah pembelajaran pengenalan untuk ramalan trajektori! Pengetahuan berkaitan pengenalan 1. Adakah kertas pratonton teratur? A: Tengok survey dulu, hlm
 SIMPL: Penanda aras ramalan gerakan berbilang ejen yang mudah dan cekap untuk pemanduan autonomi
Feb 20, 2024 am 11:48 AM
SIMPL: Penanda aras ramalan gerakan berbilang ejen yang mudah dan cekap untuk pemanduan autonomi
Feb 20, 2024 am 11:48 AM
Tajuk asal: SIMPL: ASimpleandEfficientMulti-agentMotionPredictionBaselineforAutonomousDriving Paper pautan: https://arxiv.org/pdf/2402.02519.pdf Pautan kod: https://github.com/HKUST-Aerial-Robotics/SIMPL Unit pengarang: Universiti Sains Hong Kong dan Teknologi Idea Kertas DJI: Kertas kerja ini mencadangkan garis dasar ramalan pergerakan (SIMPL) yang mudah dan cekap untuk kenderaan autonomi. Berbanding dengan agen-sen tradisional
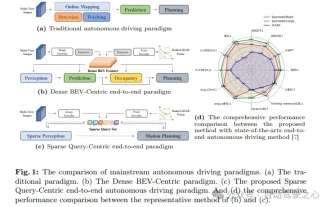 SOTA terbaharu nuScenes |. SparseAD: Pertanyaan jarang membantu pemanduan autonomi hujung ke hujung yang cekap!
Apr 17, 2024 pm 06:22 PM
SOTA terbaharu nuScenes |. SparseAD: Pertanyaan jarang membantu pemanduan autonomi hujung ke hujung yang cekap!
Apr 17, 2024 pm 06:22 PM
Ditulis di hadapan & titik permulaan Paradigma hujung ke hujung menggunakan rangka kerja bersatu untuk mencapai pelbagai tugas dalam sistem pemanduan autonomi. Walaupun kesederhanaan dan kejelasan paradigma ini, prestasi kaedah pemanduan autonomi hujung ke hujung pada subtugas masih jauh ketinggalan berbanding kaedah tugasan tunggal. Pada masa yang sama, ciri pandangan mata burung (BEV) padat yang digunakan secara meluas dalam kaedah hujung ke hujung sebelum ini menyukarkan untuk membuat skala kepada lebih banyak modaliti atau tugasan. Paradigma pemanduan autonomi hujung ke hujung (SparseAD) tertumpu carian jarang dicadangkan di sini, di mana carian jarang mewakili sepenuhnya keseluruhan senario pemanduan, termasuk ruang, masa dan tugas, tanpa sebarang perwakilan BEV yang padat. Khususnya, seni bina jarang bersatu direka bentuk untuk kesedaran tugas termasuk pengesanan, penjejakan dan pemetaan dalam talian. Di samping itu, berat
 Mari kita bincangkan tentang sistem pemanduan autonomi hujung ke hujung dan generasi seterusnya, serta beberapa salah faham tentang pemanduan autonomi hujung ke hujung?
Apr 15, 2024 pm 04:13 PM
Mari kita bincangkan tentang sistem pemanduan autonomi hujung ke hujung dan generasi seterusnya, serta beberapa salah faham tentang pemanduan autonomi hujung ke hujung?
Apr 15, 2024 pm 04:13 PM
Pada bulan lalu, atas sebab-sebab yang diketahui umum, saya telah mengadakan pertukaran yang sangat intensif dengan pelbagai guru dan rakan sekelas dalam industri. Topik yang tidak dapat dielakkan dalam pertukaran secara semula jadi adalah hujung ke hujung dan Tesla FSDV12 yang popular. Saya ingin mengambil kesempatan ini untuk menyelesaikan beberapa buah fikiran dan pendapat saya pada masa ini untuk rujukan dan perbincangan anda. Bagaimana untuk mentakrifkan sistem pemanduan autonomi hujung ke hujung, dan apakah masalah yang sepatutnya dijangka diselesaikan hujung ke hujung? Menurut definisi yang paling tradisional, sistem hujung ke hujung merujuk kepada sistem yang memasukkan maklumat mentah daripada penderia dan secara langsung mengeluarkan pembolehubah yang membimbangkan tugas. Sebagai contoh, dalam pengecaman imej, CNN boleh dipanggil hujung-ke-hujung berbanding kaedah pengekstrak ciri + pengelas tradisional. Dalam tugas pemanduan autonomi, masukkan data daripada pelbagai penderia (kamera/LiDAR



