 Peranti teknologi
Peranti teknologi
 AI
AI
 Bincangkan analisis perancangan laluan algoritma pencarian laluan dan pelaksanaan kod
Bincangkan analisis perancangan laluan algoritma pencarian laluan dan pelaksanaan kod
Bincangkan analisis perancangan laluan algoritma pencarian laluan dan pelaksanaan kod

Algoritma pencari laluan adalah salah satu algoritma yang biasa digunakan dalam bidang grafik komputer dan kecerdasan buatan, digunakan untuk mengira laluan terpendek atau laluan optimum dari satu titik ke titik lain. Dalam artikel ini, saya akan memperkenalkan secara terperinci dua algoritma pencarian laluan yang biasa digunakan: algoritma Dijkstra dan algoritma A*
Algoritma Dijkstra
Algoritma Dijkstra ialah kaedah keluasan yang digunakan untuk mencari laluan terpendek antara dua titik yang diprioritkan dalam graf algoritma carian. Ia berfungsi seperti berikut:
Kita perlu mencipta set S untuk menyimpan bucu yang telah menemui laluan terpendek
Kita perlu mencipta set Q untuk menyimpan bucu yang belum menemui laluan terpendek
Dalam pemulaan Apabila menggunakan dist tatasusunan jarak, anda perlu menetapkan jarak dari titik permulaan ke titik lain kepada infiniti, dan jarak dari titik permulaan ke dirinya sendiri kepada 0
Ulang langkah berikut sehingga set Q kosong:
- dalam Cari bucu u paling hampir dengan titik permulaan dalam set Q dan tambahkannya pada set S.
- Untuk setiap jiran bucu v bucu u, kemas kini jarak dist[v] dari titik permulaan ke v. Jika dist[v] > dist[u] + edge(u, v), kemas kini dist[v] ialah dist[u] + tepi(u, v).
Akhir sekali, tatasusunan dist menyimpan laluan terpendek dari titik permulaan ke setiap bucu
Berikut ialah kod sumber algoritma Dijkstra yang ditulis dalam C#:
rreeeAlgoritma ARREEE
Algoritma ialah algoritma carian heuristik yang digunakan untuk mencari laluan terpendek antara dua titik dalam graf. Idea algoritma adalah seperti berikut:
Buat baris gilir keutamaan openSet untuk menyimpan bucu yang akan diterokai
Kita perlu mencipta tatasusunan bernama gScore untuk menyimpan kos sebenar dari titik permulaan kepada setiap vertex
Kita perlu mencipta tatasusunan bernama fScore untuk menyimpan anggaran kos dari titik permulaan ke titik sasaran
Tambahkan titik permulaan pada openSet, tetapkan gScore[start] kepada 0 dan tetapkan fScore[start ] untuk memulakan Anggaran kos dari titik mula ke titik sasaran
Ulang langkah berikut sehingga openSet kosong:
- Cari arus bucu dengan fScore terkecil dalam openSet.
- Jika arus sama dengan titik sasaran, ini bermakna laluan terpendek telah ditemui dan laluan dikembalikan.
- Alih keluar arus daripada openSet.
- Untuk setiap jiran bucu jiran arus, hitung kos sebenar tempGScore dari titik permulaan ke jiran Jika tempGScore kurang daripada gScore[jiran], kemas kini gScore[jiran] kepada tempGScore dan hitung fScore[jiran] =. gScore[jiran] + anggaran kos. Jika jiran tiada dalam openSet, tambahkannya pada openSet.
Jika openSet kosong, ini bermakna titik sasaran tidak boleh dicapai, dan nilai nol dikembalikan
Berikut ialah kod sumber algoritma A* yang ditulis dalam Java:
class DijkstraAlgorithm
{
private int[,] graph;
private int size;
public DijkstraAlgorithm(int[,] graph)
{
this.graph = graph;
this.size = graph.GetLength(0);
}
public int[] FindShortestPath(int start, int end)
{
int[] dist = new int[size];
bool[] visited = new bool[size];
for (int i = 0; i <span><br> Di atas ialah perbandingan algoritma Dijkstra dan A* Pengenalan terperinci kepada algoritma, termasuk idea algoritma, proses dan kod sumber yang dilaksanakan dalam C# atau Java. Kedua-dua algoritma adalah algoritma pencari laluan yang biasa digunakan dan boleh dipilih dan digunakan mengikut keperluan khusus. </span>Sudah tentu, di bandar hari ini, perisian navigasi boleh merancang sesuatu untuk kita. 🎜Atas ialah kandungan terperinci Bincangkan analisis perancangan laluan algoritma pencarian laluan dan pelaksanaan kod. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

Video Face Swap
Tukar muka dalam mana-mana video dengan mudah menggunakan alat tukar muka AI percuma kami!

Artikel Panas

Alat panas

Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma

SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan

Hantar Studio 13.0.1
Persekitaran pembangunan bersepadu PHP yang berkuasa

Dreamweaver CS6
Alat pembangunan web visual

SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)

Topik panas
 1389
1389
 52
52
 Top 5 Genai dilancarkan pada Februari 2025: GPT-4.5, Grok-3 & More!
Mar 22, 2025 am 10:58 AM
Top 5 Genai dilancarkan pada Februari 2025: GPT-4.5, Grok-3 & More!
Mar 22, 2025 am 10:58 AM
Februari 2025 telah menjadi satu lagi bulan yang berubah-ubah untuk AI generatif, membawa kita beberapa peningkatan model yang paling dinanti-nantikan dan ciri-ciri baru yang hebat. Dari Xai's Grok 3 dan Anthropic's Claude 3.7 Sonnet, ke Openai's G
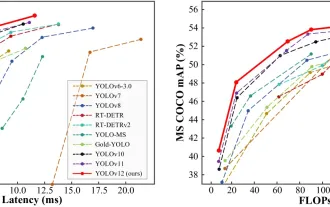 Bagaimana cara menggunakan Yolo V12 untuk pengesanan objek?
Mar 22, 2025 am 11:07 AM
Bagaimana cara menggunakan Yolo V12 untuk pengesanan objek?
Mar 22, 2025 am 11:07 AM
Yolo (anda hanya melihat sekali) telah menjadi kerangka pengesanan objek masa nyata yang terkemuka, dengan setiap lelaran bertambah baik pada versi sebelumnya. Versi terbaru Yolo V12 memperkenalkan kemajuan yang meningkatkan ketepatan
 Penjana Seni AI Terbaik (Percuma & amp; Dibayar) untuk projek kreatif
Apr 02, 2025 pm 06:10 PM
Penjana Seni AI Terbaik (Percuma & amp; Dibayar) untuk projek kreatif
Apr 02, 2025 pm 06:10 PM
Artikel ini mengkaji semula penjana seni AI atas, membincangkan ciri -ciri mereka, kesesuaian untuk projek kreatif, dan nilai. Ia menyerlahkan Midjourney sebagai nilai terbaik untuk profesional dan mengesyorkan Dall-E 2 untuk seni berkualiti tinggi dan disesuaikan.
 Adakah chatgpt 4 o tersedia?
Mar 28, 2025 pm 05:29 PM
Adakah chatgpt 4 o tersedia?
Mar 28, 2025 pm 05:29 PM
CHATGPT 4 kini tersedia dan digunakan secara meluas, menunjukkan penambahbaikan yang ketara dalam memahami konteks dan menjana tindak balas yang koheren berbanding dengan pendahulunya seperti ChATGPT 3.5. Perkembangan masa depan mungkin merangkumi lebih banyak Inter yang diperibadikan
 CHATBOTS AI terbaik berbanding (Chatgpt, Gemini, Claude & amp; Lagi)
Apr 02, 2025 pm 06:09 PM
CHATBOTS AI terbaik berbanding (Chatgpt, Gemini, Claude & amp; Lagi)
Apr 02, 2025 pm 06:09 PM
Artikel ini membandingkan chatbots AI seperti Chatgpt, Gemini, dan Claude, yang memberi tumpuan kepada ciri -ciri unik mereka, pilihan penyesuaian, dan prestasi dalam pemprosesan bahasa semula jadi dan kebolehpercayaan.
 Bermula dengan Meta Llama 3.2 - Analytics Vidhya
Apr 11, 2025 pm 12:04 PM
Bermula dengan Meta Llama 3.2 - Analytics Vidhya
Apr 11, 2025 pm 12:04 PM
Meta's Llama 3.2: Lompat ke hadapan dalam Multimodal dan Mobile AI META baru -baru ini melancarkan Llama 3.2, kemajuan yang ketara dalam AI yang memaparkan keupayaan penglihatan yang kuat dan model teks ringan yang dioptimumkan untuk peranti mudah alih. Membina kejayaan o
 Pembantu Menulis AI Teratas untuk Meningkatkan Penciptaan Kandungan Anda
Apr 02, 2025 pm 06:11 PM
Pembantu Menulis AI Teratas untuk Meningkatkan Penciptaan Kandungan Anda
Apr 02, 2025 pm 06:11 PM
Artikel ini membincangkan pembantu penulisan AI terkemuka seperti Grammarly, Jasper, Copy.ai, WriteSonic, dan Rytr, yang memberi tumpuan kepada ciri -ciri unik mereka untuk penciptaan kandungan. Ia berpendapat bahawa Jasper cemerlang dalam pengoptimuman SEO, sementara alat AI membantu mengekalkan nada terdiri
 Cara Menggunakan Mistral OCR untuk Model RAG Seterusnya
Mar 21, 2025 am 11:11 AM
Cara Menggunakan Mistral OCR untuk Model RAG Seterusnya
Mar 21, 2025 am 11:11 AM
Mistral OCR: Merevolusi Generasi Pengambilan Pengambilan semula dengan Pemahaman Dokumen Multimodal Sistem Generasi Pengambilan Retrieval (RAG) mempunyai keupayaan AI yang ketara, membolehkan akses ke kedai data yang luas untuk mendapatkan respons yang lebih tepat



