Kira persilangan segi empat sama lengkung y=x dan garis lurus x=1 dalam Java menggunakan rekursi

Gunakan kaedah rekursif dalam java untuk mengira kuasa dua lengkung y x dan tepi melengkung yang dikelilingi oleh garis lurus x 1 x paksi

kelas awam Util {

utama kekosongan statik awam(String[] args) {

System.out.println(getMj(2000));

}

Kawasan pengiraan berganda statik awam(berganda n){

jika(n==1){

kembali 1.0;

}lain{

berganda r = (n-1) * (n-1) * (n+1) * (2*n+1) / (n * n * n * (2*n-1));

kembali r*getMj(n-1);

}

}

}

Prasyarat untuk algoritma rekursif ialah memahami formula amnya 2000 bermaksud membahagikan segi tiga melengkung kepada 2000 segi empat tepat boleh dilihat dalam rajah di bawah:

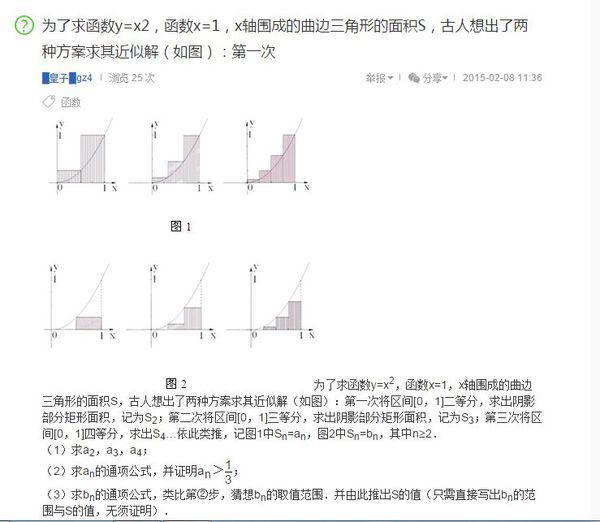
Menggunakan algoritma Rajah 1:

an=(n+1)(2n+1) /6n^2

Cara mudah untuk menulisnya adalah seperti berikut:

kelas awam Util {

utama kekosongan statik awam(String[] args) {

System.out.println(getMj(100000));

}

Kawasan pengiraan berganda statik awam(berganda n){

kembali (n+1)*(2*n+1)/(6*n*n);

}

}

masalah rekursi java

(1) Rekursi memanggil dirinya dalam prosedur atau fungsi

(2) Apabila menggunakan strategi rekursif, anda mesti memastikan bahawa terdapat keadaan akhir rekursif yang jelas, juga dikenali sebagai jalan keluar rekursif.

Algoritma rekursif biasanya digunakan untuk menyelesaikan tiga jenis masalah:

(1) Takrif data ditakrifkan secara rekursif. (Fungsi Fibonacci)

(2) Penyelesaian masalah dilaksanakan mengikut algoritma rekursif. (Traceback)

(3) Bentuk struktur data ditakrifkan secara rekursif.

Contoh berikut mengira pemfaktoran n secara rekursif.

Ujian kelas awam {

faktorial int statik awam(int n) {

jika(n == 0){

kembali 1;

}lain{

kembali n * faktorial(n-1);

}

}

utama kekosongan statik awam(String[] args) {

System.out.println(faktorial(3));

}

}

Algoritma rekursif untuk mengurangkan separuh carian dalam struktur data Java memerlukan bimbingan pakar!

pakej souce;

Cari kelas awam {

Cari binari boolean statik awam(int[] a, int x, int kiri, int kanan) { // Kaedah utama carian binari // ... }

jika (x == a[kiri] || x == a[kanan]) { kembali benar; // Ditemui, kembali benar }

Jika keputusan (kanan-kiri) ialah nombor negatif, bermakna nilai di sebelah kanan adalah lebih kecil daripada nilai di sebelah kiri.

int mid = (kiri+kanan)/2; //jika tidak: dua mata

jika(x == a[pertengahan]) kembalikan benar; // Cari elemen tengah dan kembalikan benar

lain{ //sebaliknya

Jika x lebih besar daripada elemen tengah, kembalikan fungsi carian binari (binarySearch) dan teruskan mencari x di separuh kanan tatasusunan (a), iaitu binarySearch(a,x,mid+1,right) . Ini boleh mengecilkan skop carian dan meningkatkan kecekapan carian.

else return binarySearch(a, x, left, mid-1); // Jika nilai sasaran kurang daripada elemen tengah, teruskan carian di bahagian kiri.

}

}

isihan int[] akhir statik awam (int[] a) { // Ini ialah kaedah yang digunakan untuk mengisih tatasusunan integer // Anda boleh menggunakan sebarang algoritma pengisihan, seperti isihan gelembung, isihan sisipan, isihan pemilihan, isihan pantas, dsb. // Di sini kita menggunakan isihan gelembung untuk mengisih tatasusunan untuk (int i = 0; i a[j + 1]) { // Tukar kedudukan elemen int temp = a[j];

untuk (int i = 0; i

untuk (int j = 0; j

jika(a[i]

tukar(a,i,j);

}

}

}

kembali a;

}

Pertukaran kekosongan statik peribadi(int[] a, int i, int j) { //Tentukan pertukaran fungsi statik peribadi untuk menukar kedudukan elemen yang dilanggan i dan j dalam tatasusunan a

int temp = a[i];

a[i] = a[j];

a[j] = suhu;

}

cetakan kosong statik awam(int[] a) { //Fungsi cetak untuk (int i = 0; i

System.out.println();

untuk (int i = 0; i

System.out.print(a[i]);

jika(i!=a.panjang-1) { System.out.print(","); }

}

System.out.println();

}

utama kekosongan statik awam(String[] args) { //Kaedah ujian

int[] a = {90, 12, 21, 32, 51, 78, 87, 98} ialah tatasusunan yang mengandungi 8 integer.

cetak(isih(a));

System.out.println(binarySearch(sort(a), 40, 0, a.length-1)); ialah kod yang digunakan untuk carian binari untuk elemen dengan nilai 40 dalam tatasusunan a.

}

}

Atas ialah kandungan terperinci Kira persilangan segi empat sama lengkung y=x dan garis lurus x=1 dalam Java menggunakan rekursi. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!