
Artikel sebelum ini bercakap tentang kaedah arka kanvas, dan artikel ini bercakap tentang kaedah arka yang berkaitan dengannya.
arka dan arcTo adalah serupa daripada nama mereka. arcTo juga merupakan kaedah melukis lengkung, dan lengkung yang dilukisnya juga merupakan lengkok bulatan sempurna. Tetapi parameternya tidak serasi dengan arka~
ctx.arcTo(x1,y1,x2,y2,radius); hanya parameter terakhir ialah jejari bulatan, menunjukkan bahawa arcTo mempunyai beberapa hubungan dengan bulatan.
Terdapat sedikit artikel tentang arcTo di Internet, dan akhirnya saya menemui satu dari negara asing dan tiada alat intuitif untuk lukisan kanvas, jadi saya hanya boleh bergantung pada meneka arcTo membuat saya meneka untuk masa yang lama . .
Untuk penerangan intuitif, saya menggunakan kaedah tambahan: di mana sahaja arcTo dilukis, saya juga menggunakan lineTo untuk melukis titik yang sepadan untuk melihat hubungan mereka. Hanya lukis garisan tambahan.
Jom jadikan bola lebih besar! 

Izinkan saya menggunakan pengetahuan saya tentang geometri yang tidak terdapat pada jadual untuk mengesahkan cadangan ini. Untuk memudahkan pengiraan, saya mula-mula menukar sudut antara dua garisan kepada 90 darjah. 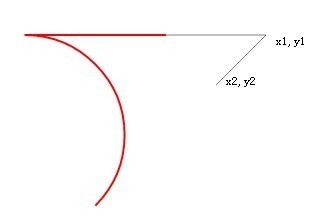
Kami menjadikan y2 lebih besar, iaitu memanjangkan garis tangen dan mengubahnya menjadi 550. Selepas menyegarkan: 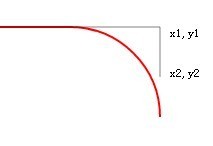
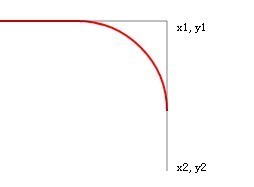 Garis tangen dilanjutkan, tetapi garisan merah yang dilukis oleh arcTo tiada perubahan.
Garis tangen dilanjutkan, tetapi garisan merah yang dilukis oleh arcTo tiada perubahan.
 Apakah kaedah penghasilan penghasilan animasi html5?
Apakah kaedah penghasilan penghasilan animasi html5?
 tahap pengasingan transaksi lalai mysql
tahap pengasingan transaksi lalai mysql
 Bagaimana untuk membeli Bitcoin
Bagaimana untuk membeli Bitcoin
 Bagaimana untuk mengeksport perkataan daripada powerdesigner
Bagaimana untuk mengeksport perkataan daripada powerdesigner
 Perbezaan antara bahasa pascal dan bahasa c
Perbezaan antara bahasa pascal dan bahasa c
 Apakah perisian untuk belajar python?
Apakah perisian untuk belajar python?
 Bagaimana untuk memadam sepenuhnya mongodb jika pemasangan gagal
Bagaimana untuk memadam sepenuhnya mongodb jika pemasangan gagal
 Cara menukar bandar di Douyin
Cara menukar bandar di Douyin




