Proses latihan algoritma pembelajaran pengukuhan (Reinforcement Learning, RL) biasanya memerlukan sejumlah besar data sampel yang berinteraksi dengan persekitaran untuk menyokongnya. Walau bagaimanapun, dalam dunia nyata, selalunya sangat mahal untuk mengumpul sejumlah besar sampel interaksi, atau keselamatan proses pensampelan tidak dapat dipastikan, seperti latihan pertempuran udara UAV dan latihan pemanduan autonomi. Masalah ini mengehadkan skop pembelajaran pengukuhan dalam banyak aplikasi praktikal. Oleh itu, penyelidik telah bekerja keras untuk meneroka bagaimana untuk mencapai keseimbangan antara kecekapan sampel dan keselamatan untuk menyelesaikan masalah ini. Satu penyelesaian yang mungkin adalah menggunakan simulator atau persekitaran maya untuk menjana sejumlah besar data sampel, dengan itu mengelakkan kos dan risiko keselamatan situasi dunia sebenar. Di samping itu, untuk meningkatkan kecekapan sampel algoritma pembelajaran pengukuhan semasa proses latihan, beberapa penyelidik telah menggunakan teknologi pembelajaran perwakilan untuk mereka bentuk tugas tambahan untuk meramal isyarat keadaan masa hadapan. Dengan cara ini, algoritma boleh mengekstrak dan mengekodkan ciri yang berkaitan dengan keputusan masa depan daripada keadaan persekitaran asal. Tujuan pendekatan ini adalah untuk meningkatkan prestasi algoritma pembelajaran pengukuhan dengan mempelajari lebih banyak maklumat tentang alam sekitar dan menyediakan asas yang lebih baik untuk membuat keputusan. Dengan cara ini, algoritma boleh menggunakan data sampel dengan lebih cekap semasa proses latihan, mempercepatkan proses pembelajaran, dan meningkatkan ketepatan dan kecekapan membuat keputusan.
Berdasarkan idea ini, kerja ini mereka bentuk tugas tambahan untuk meramalkan menyatakan taburan domain kekerapan jujukan
untuk pelbagai langkah pada masa hadapan untuk menangkap ciri-ciri membuat keputusan masa depan jangka panjang dan dengan itu meningkatkan kecekapan sampel algoritma .Karya ini bertajuk State Sequences Prediction via Fourier Transform for Representation Learning, diterbitkan dalam NeurIPS 2023, dan diterima sebagai Spotlight.
Senarai pengarang: Ye Mingxuan, Kuang Yufei, Wang Jie*, Yang Rui, Zhou Wengang, Li Houqiang, Wu Feng
Pautan kertas: https://openreview.net/forum? MvoMDD6emT
Pautan kod: https://github.com/MIRALab-USTC/RL-SPF/
Latar belakang dan motivasi penyelidikan
Untuk meningkatkan kecekapan sampel, penyelidik telah mula memberi tumpuan kepada pembelajaran perwakilan, dengan harapan bahawa perwakilan yang diperolehi melalui latihan dapat mengekstrak maklumat ciri yang kaya dan berguna daripada keadaan asal persekitaran, dengan itu meningkatkan kecekapan penerokaan robot dalam ruang negeri.
Rangka kerja algoritma pembelajaran pengukuhan berdasarkan pembelajaran perwakilan
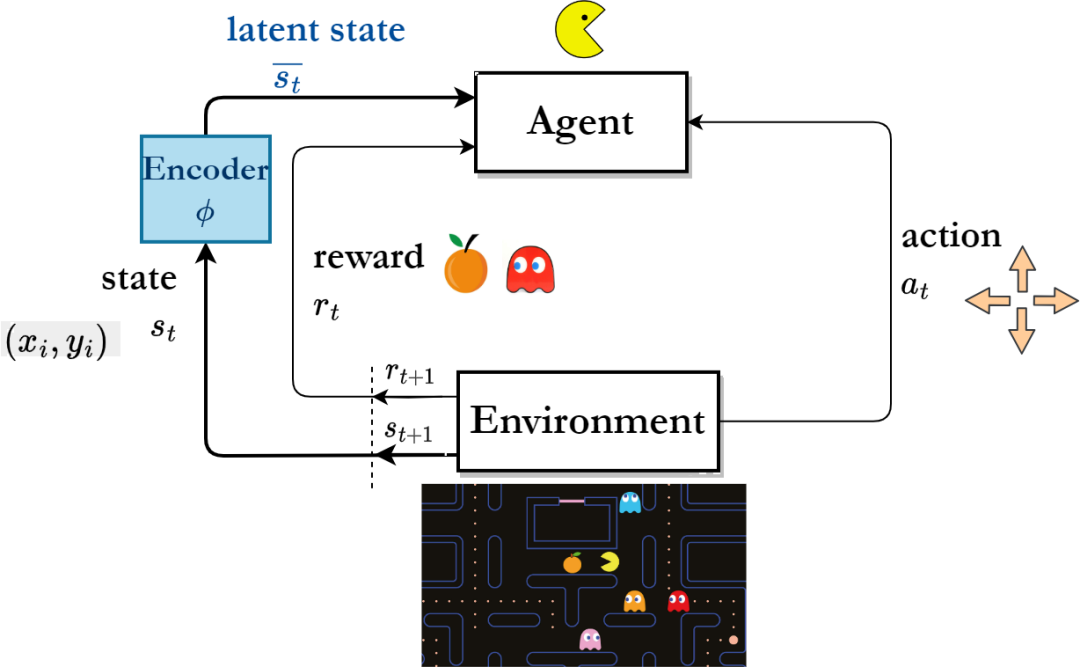
"isyarat jujukan jangka panjang"mengandungi lebih banyak maklumat masa depan untuk membuat keputusan yang bermanfaat berbanding jangka panjang kepada isyarat satu langkah. Diilhamkan oleh sudut pandangan ini, beberapa penyelidik telah mencadangkan untuk membantu pembelajaran perwakilan dengan meramalkan isyarat urutan keadaan berbilang langkah pada masa hadapan [4,5]. Walau bagaimanapun, adalah sangat sukar untuk meramalkan urutan keadaan secara langsung untuk membantu pembelajaran perwakilan.
Antara dua kaedah sedia ada, satu kaedah menjana keadaan masa hadapan secara beransur-ansur pada satu masa dengan mempelajari model peralihan kebarangkalian satu langkah untuk secara tidak langsung meramalkan urutan keadaan berbilang langkah [6,7]. Walau bagaimanapun, kaedah jenis ini memerlukan ketepatan tinggi model pemindahan kebarangkalian terlatih, kerana ralat ramalan pada setiap langkah akan terkumpul apabila panjang jujukan ramalan meningkat.
Satu lagi jenis kaedah membantu pembelajaran perwakilan [8] dengan meramalkan secara langsung urutan keadaan berbilang langkah pada masa hadapan[8], tetapi kaedah jenis ini perlu menyimpan jujukan keadaan sebenar berbilang langkah sebagai label tugas ramalan, yang menggunakan sejumlah besar storan . Oleh itu, cara mengekstrak maklumat masa depan dengan berkesan yang bermanfaat untuk membuat keputusan jangka panjang daripada urutan keadaan persekitaran dan dengan itu meningkatkan kecekapan sampel semasa latihan robot kawalan berterusan adalah masalah yang perlu diselesaikan.
Untuk menyelesaikan masalah di atas, kami mencadangkan kaedah pembelajaran perwakilan berdasarkan ramalan domain frekuensi jujukan keadaan (STate Sequences P
rediction melaluiFourier Transform, SPF). untuk menggunakan "Taburan domain kekerapan bagi jujukan keadaan" untuk mengekstrak maklumat arah aliran dan keteraturan secara eksplisit dalam data jujukan keadaan, dengan itu membantu perwakilan mengekstrak maklumat masa depan jangka panjang dengan cekap. Kami secara teorinya telah membuktikan bahawa terdapat "dua jenis maklumat struktur" dalam urutan keadaan Satu ialah maklumat trend yang berkaitan dengan prestasi strategi, dan satu lagi Maklumat keteraturan berkaitan dengan status berkala. Sebelum menganalisis dua maklumat struktur secara terperinci, kami mula-mula memperkenalkan takrifan Proses Keputusan Markov (MDP) yang berkaitan yang menjana jujukan keadaan. Kami menganggap proses keputusan Markov klasik dalam masalah kawalan berterusan, yang boleh diwakili oleh lima kali ganda. Antaranya, ialah keadaan dan ruang tindakan yang sepadan, ialah fungsi ganjaran, ialah fungsi peralihan keadaan persekitaran, ialah taburan awal keadaan, dan merupakan faktor diskaun. Selain itu, kami gunakan untuk mewakili pengedaran tindakan dasar dalam negeri . . Kami merekodkan trajektori yang sepadan dengan keadaan dan tindakan yang diperoleh semasa interaksi antara ejen dan persekitaran sebagai , dan trajektori mematuhi pengedaran . Matlamat algoritma pembelajaran pengukuhan adalah untuk memaksimumkan pulangan terkumpul yang dijangkakan pada masa hadapan yang kami gunakan untuk mewakili pulangan terkumpul purata di bawah model strategi dan persekitaran semasa, dan disingkatkan sebagai , yang ditakrifkan seperti berikut: . menunjukkan prestasi strategi semasa. Maklumat trend Dalam tugasan pembelajaran pengukuhan, urutan keadaan masa hadapan sebahagian besarnya menentukan urutan tindakan yang diambil oleh ejen pada masa hadapan, dan seterusnya menentukan urutan ganjaran yang sepadan. Oleh itu, jujukan keadaan masa hadapan bukan sahaja mengandungi maklumat tentang fungsi peralihan kebarangkalian yang wujud dalam persekitaran, tetapi juga boleh membantu dalam menangkap arah aliran strategi semasa.
Teorem 1: Jika fungsi ganjaran hanya berkaitan dengan keadaan, maka untuk mana-mana dua strategi dan , perbezaan prestasi mereka boleh dikawal oleh perbezaan dalam pengagihan jujukan keadaan yang dijana oleh dua strategi ini: Dalam formula di atas, mewakili taburan kebarangkalian jujukan keadaan di bawah syarat strategi yang ditentukan dan fungsi kebarangkalian peralihan, dan mewakili norma. Sebaliknya, dalam keadaan tertentu, perbezaan taburan domain frekuensi bagi jujukan keadaan juga boleh memberikan had atas untuk perbezaan prestasi dasar yang sepadan, seperti yang ditunjukkan dalam teorem berikut:
Teorem 2 : Jika keadaan Ruang adalah dimensi terhingga dan fungsi ganjaran ialah polinomial n-darjah yang berkaitan dengan keadaan, maka untuk mana-mana dua strategi dan , perbezaan prestasi mereka boleh dikawal oleh perbezaan dalam taburan domain kekerapan bagi jujukan keadaan yang dijana. dengan dua strategi ini: Dalam formula di atas, mewakili fungsi Fourier bagi jujukan kuasa bagi jujukan keadaan yang dijana oleh polisi , dan mewakili komponen ke-fungsi Fourier. jujukan keadaan masih mengandungi ciri yang berkaitan dengan prestasi dasar semasa. Maklumat biasa Dalam banyak tugasan senario sebenar, ejen juga akan menunjukkan tingkah laku berkala kerana fungsi peralihan keadaan persekitaran mereka sendiri berkala. Ambil robot pemasangan industri sebagai contoh Robot dilatih untuk memasang bahagian bersama-sama untuk mencipta produk akhir Apabila latihan strategi mencapai kestabilan, ia melakukan urutan tindakan berkala yang membolehkannya memasang bahagian dalam Bersama dengan cekap. Diilhamkan oleh contoh di atas, kami menyediakan beberapa analisis teori untuk membuktikan bahawa dalam ruang keadaan terhingga, apabila matriks kebarangkalian peralihan memenuhi andaian tertentu, jujukan keadaan yang sepadan mungkin menunjukkan "secara beransur-ansur" apabila ejen mencapai strategi yang stabil . Hampir berkala", teorem khusus adalah seperti berikut: Teorem 3: Untuk ruang keadaan dimensi terhingga dengan matriks peralihan keadaan , dengan mengandaikan bahawa terdapat kelas kitaran, submatriks peralihan keadaan yang sepadan ialah. Anggapkan bahawa bilangan nilai eigen dengan modulus 1 matriks ini ialah, maka untuk taburan awal mana-mana keadaan, taburan keadaan menunjukkan berkala tanpa gejala dengan tempoh. Dalam tugas MuJoCo, apabila latihan polisi mencapai kestabilan, ejen juga akan menunjukkan pergerakan berkala. Rajah di bawah memberikan contoh urutan keadaan ejen HalfCheetah dalam tugas MuJoCo dalam satu tempoh masa, dan keberkalaan yang jelas boleh diperhatikan. (Untuk lebih banyak contoh jujukan keadaan berkala dalam tugas MuJoCo, sila rujuk Bahagian E dalam lampiran kertas ini) Pengenalan kepada kaedah Dalam bahagian sebelumnya, kami secara teorinya membuktikan bahawa taburan domain frekuensi urutan keadaan dapat mencerminkan prestasi strategi, dan dengan menganalisis komponen frekuensi dalam domain frekuensi kami dapat secara eksplisit. menangkap ciri berkala urutan keadaan. untuk menggalakkan perwakilan mengekstrak maklumat struktur dalam jujukan keadaan. Fungsi kehilangan kaedah SPFBerikut memperkenalkan pemodelan kami bagi tugas tambahan ini. Memandangkan keadaan dan tindakan semasa, kami mentakrifkan jangkaan jujukan keadaan masa hadapan seperti berikut: Tugas tambahan kami melatih perwakilan untuk meramalkan transformasi Fourier masa diskret (DTFT) jangkaan jujukan keadaan di atas ), yang ialah, Rumus transformasi Fourier di atas boleh ditulis semula sebagai bentuk rekursif berikut: di mana
Diinspirasikan oleh fungsi kehilangan ralat TD [9] yang mengoptimumkan rangkaian nilai Q dalam pembelajaran Q, kami mereka bentuk fungsi kehilangan berikut: Antaranya, dan ialah parameter rangkaian neural pengekod perwakilan (pengekod) dan peramal fungsi Fourier (peramal) yang mana fungsi kehilangan perlu dioptimumkan, dan merupakan kumpulan pengalaman untuk menyimpan data sampel. Selanjutnya, kita boleh membuktikan bahawa formula rekursif di atas boleh dinyatakan sebagai peta mampatan: Teorem 4: Biar mewakili keluarga fungsi , dan tentukan norma pada mewakili vektor baris matriks . Kami mentakrifkan pemetaan sebagai dan boleh dibuktikan itu adalah pemetaan mampatan. Mengikut prinsip pemetaan mampatan, kami boleh menggunakan operator secara berulang untuk menganggarkan taburan domain frekuensi bagi jujukan keadaan sebenar, dan mempunyai jaminan penumpuan dalam tetapan jadual. Selain itu, fungsi kehilangan yang kami reka hanya bergantung pada keadaan saat semasa dan detik seterusnya, jadi tidak perlu menyimpan data keadaan beberapa langkah pada masa hadapan sebagai label ramalan, yang mempunyai kelebihan daripada "pelaksanaan mudah dan volum storan rendah" Di bawah kami memperkenalkan rangka kerja algoritma kaedah (SPF) dalam kertas kerja ini. Kami memasukkan data tindakan keadaan semasa dan detik seterusnya ke dalam talian (dalam talian) dan sasaran ( sasaran) masing-masing ) Dalam pengekod perwakilan (pengekod), data perwakilan tindakan keadaan diperoleh, dan kemudian data perwakilan dimasukkan ke peramal fungsi Fourier (peramal) untuk mendapatkan dua set urutan keadaan ramalan fungsi Fourier pada momen semasa dan nilai detik seterusnya. Dengan menggantikan dua set ramalan fungsi Fourier ini, kita boleh mengira nilai fungsi kehilangan. Kami mengoptimumkan dan mengemas kini pengekod perwakilan dan peramal fungsi Fourier dengan meminimumkan fungsi kehilangan, supaya output peramal boleh menghampiri transformasi Fourier bagi urutan keadaan sebenar, dengan itu menggalakkan pengekod perwakilan untuk mengekstrak ciri yang mengandungi masa depan jangka panjang Ciri-ciri maklumat struktur jujukan keadaan. Kami memasukkan keadaan asal dan tindakan ke dalam pengekod perwakilan, menggunakan ciri yang diperolehi sebagai input rangkaian pelakon dan rangkaian pengkritik dalam algoritma pembelajaran pengukuhan, dan menggunakan algoritma pembelajaran pengukuhan klasik untuk mengoptimumkan rangkaian pelakon dan pengkritik rangkaian. Hasil eksperimen (Nota: Bahagian ini hanya memilih sebahagian daripada keputusan eksperimen. Untuk keputusan yang lebih terperinci, sila rujuk Bahagian 6 dan lampiran kertas asal.)
Angka di atas menunjukkan lengkung prestasi kaedah SPF yang dicadangkan kami (garisan merah dan garis oren) dan kaedah perbandingan lain dalam 6 tugasan MuJoCo. Keputusan menunjukkan bahawa kaedah cadangan kami boleh mencapai peningkatan prestasi sebanyak 19.5% berbanding kaedah lain. Kami menjalankan eksperimen ablasi pada setiap modul kaedah SPF, membandingkan kaedah ini dengan tidak menggunakan modul projektor (noproj), tidak menggunakan modul rangkaian sasaran (notarg), dan menukar kehilangan ramalan (nofreqloss) , bandingkan prestasi apabila menukar struktur rangkaian pengekod ciri (mlp, mlp_cat). Rajah hasil percubaan ablasi bagi kaedah SPF yang digunakan pada algoritma SAC, diuji pada tugas HalfCheetah Kami menggunakan kaedah Fuse atau output SPF fungsi Fourier jujukan keadaan, dan jujukan keadaan 200 langkah yang dipulihkan melalui Transformasi Fourier Songsang dibandingkan dengan jujukan keadaan 200 langkah yang sebenar. Rajah skematik jujukan keadaan dipulihkan berdasarkan nilai ramalan fungsi Fourier, diuji pada tugas Walker2d. Antaranya, garis biru ialah gambar rajah skema bagi jujukan keadaan sebenar, dan lima garis merah ialah gambar rajah skematik jujukan keadaan yang dipulihkan Garis merah yang lebih rendah dan lebih ringan mewakili jujukan keadaan yang dipulihkan dengan menggunakan keadaan sejarah yang lebih panjang. Analisis maklumat struktur dalam urutan keadaan
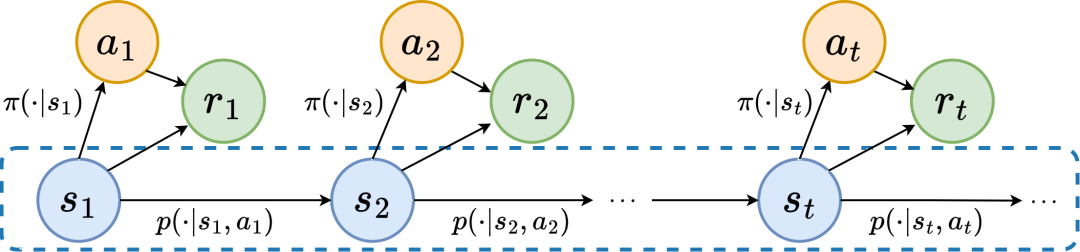
Proses Keputusan Markov
Di bawah ini kami memperkenalkan "ciri struktur pertama" jujukan keadaan, yang melibatkan pergantungan antara jujukan negeri dan jujukan ganjaran yang sepadan, dan boleh menunjukkan prestasi strategi semasa. Trend
. 
"ciri struktur kedua" yang wujud dalam urutan keadaan, yang melibatkan pergantungan masa antara isyarat keadaan, iaitu urutan keadaan dalam jangka masa yang panjang. corak biasa
dipamerkan.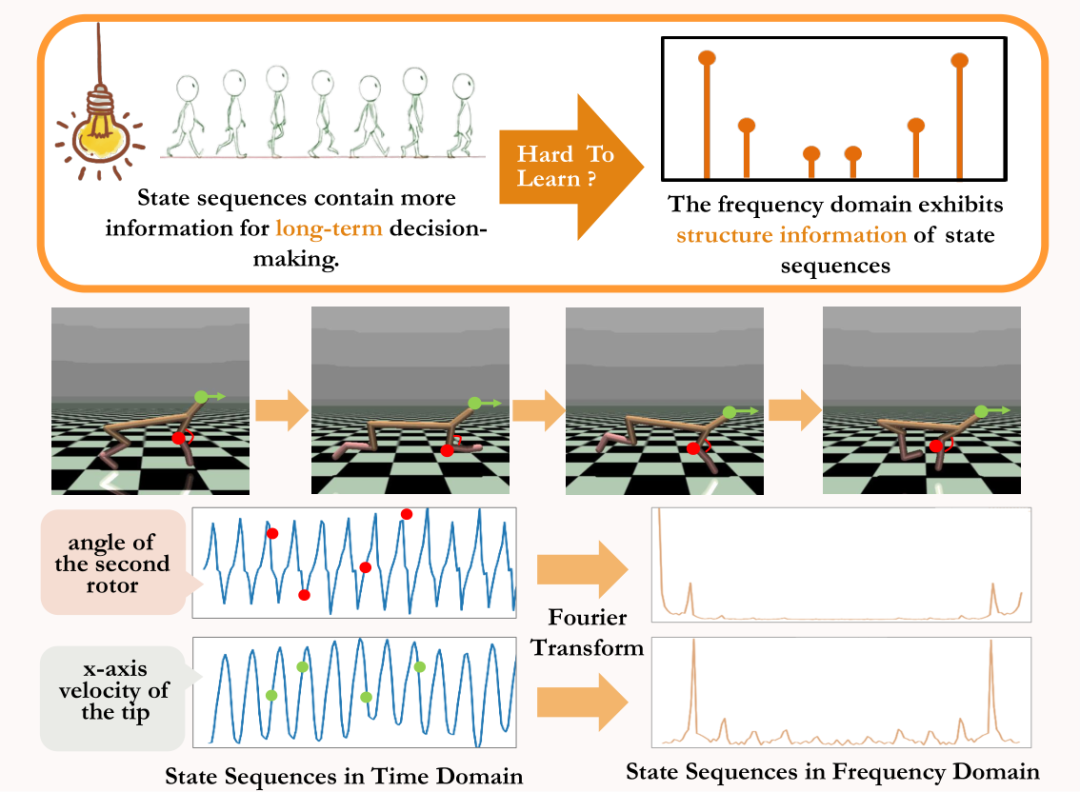 
Maklumat yang dipersembahkan oleh siri masa dalam domain masa agak berselerak, tetapi dalam domain frekuensi, maklumat biasa dalam jujukan dibentangkan dalam bentuk yang lebih tertumpu. Dengan menganalisis komponen frekuensi dalam domain frekuensi, kami boleh menangkap secara eksplisit ciri berkala yang terdapat dalam urutan keadaan.
Diinspirasikan oleh analisis di atas, kami mereka bentuk tugas tambahan
"Meramalkan transformasi Fourier bagi jujukan keadaan masa hadapan tak terhingga"
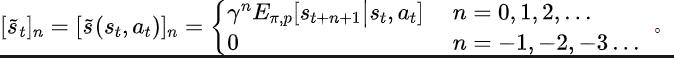
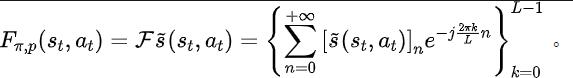
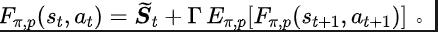
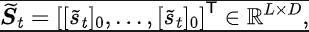
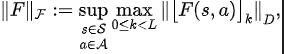
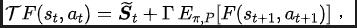
Rangka kerja algoritma kaedah SPF
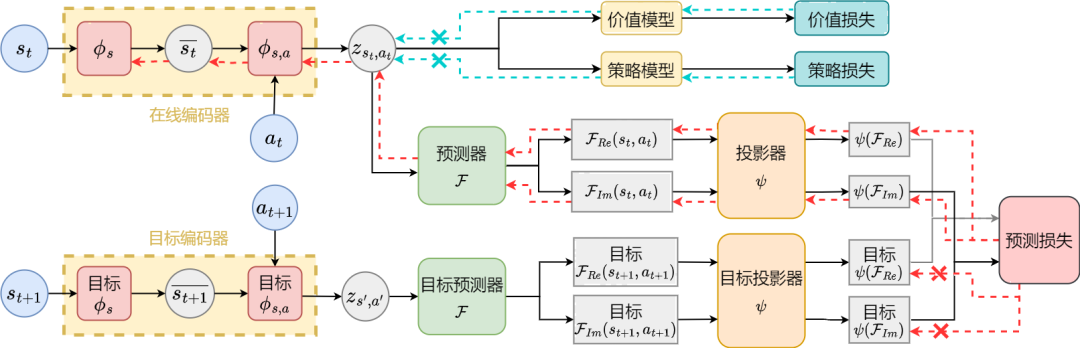
Kami akan SPF Kaedah ini telah diuji pada persekitaran kawalan robot simulasi MuJoCo, dan enam kaedah berikut telah dibandingkan:
SAC
Eksperimen ablasi
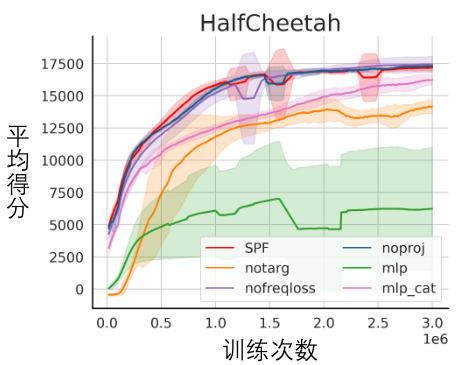
Eksperimen visualisasi
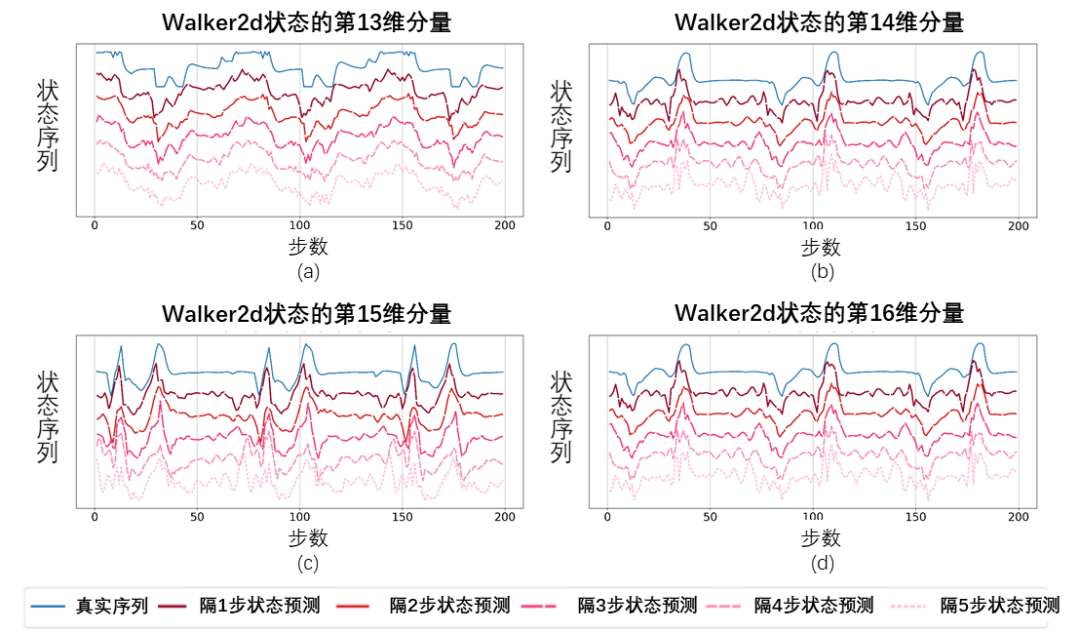
Atas ialah kandungan terperinci Universiti Sains dan Teknologi China membangunkan kaedah 'Ramalan Domain Frekuensi Urutan Negeri', yang meningkatkan prestasi sebanyak 20% dan memaksimumkan kecekapan sampel.. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
![[Web front-end] Permulaan pantas Node.js](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
