
Biar theta = parameter model dan max_iters = bilangan zaman. Untuk itr=1,2,3,...,max_iters: Untuk mini_batch(X_mini,y_mini):
Pas hadapan kumpulan X_mini:
1 Ramalkan kumpulan mini
2 parameter Kira ralat ramalan (J(theta))
Pasca penghantaran: Kira kecerunan (theta)=J(theta)wrt terbitan separa theta
Kemas kini parameter: theta=theta–learning_rate*gradient(theta)
Langkah 1: Import kebergantungan, jana data untuk regresi linear dan gambarkan data yang dijana. Ambil 8000 contoh data, setiap contoh mempunyai 2 ciri atribut. Sampel data ini dibahagikan lagi kepada set latihan (X_train, y_train) dan set ujian (X_test, y_test), dengan 7200 dan 800 sampel masing-masing.
import numpy as np import matplotlib.pyplot as plt mean=np.array([5.0,6.0]) cov=np.array([[1.0,0.95],[0.95,1.2]]) data=np.random.multivariate_normal(mean,cov,8000) plt.scatter(data[:500,0],data[:500,1],marker='.') plt.show() data=np.hstack((np.ones((data.shape[0],1)),data)) split_factor=0.90 split=int(split_factor*data.shape[0]) X_train=data[:split,:-1] y_train=data[:split,-1].reshape((-1,1)) X_test=data[split:,:-1] y_test=data[split:,-1].reshape((-1,1)) print(& quot Number of examples in training set= % d & quot % (X_train.shape[0])) print(& quot Number of examples in testing set= % d & quot % (X_test.shape[0]))
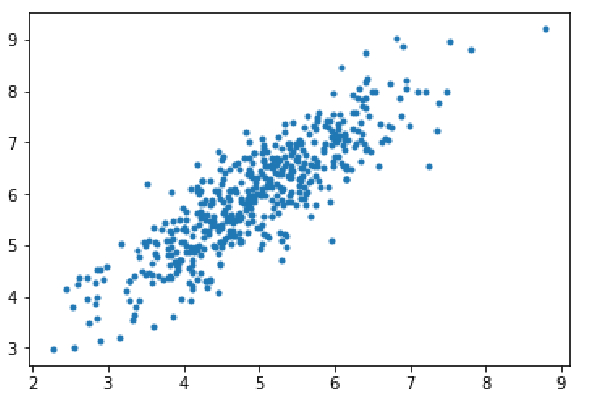
Bilangan contoh dalam set latihan = 7200 Bilangan contoh dalam set ujian = 800
Langkah 2:
Kod untuk melaksanakan regresi linear menggunakan keturunan kecerunan kelompok mini. gradientDescent() ialah fungsi pemacu utama, dan fungsi lain ialah fungsi tambahan:
Buat ramalan - hipotesis()
Kira kecerunan - gradient()
Kira ralat - kos()
Buat kumpulan mini - )
Fungsi pemacu memulakan parameter, mengira set parameter optimum untuk model dan mengembalikan parameter tersebut bersama-sama dengan senarai yang mengandungi sejarah ralat semasa parameter dikemas kini.
def hypothesis(X,theta):
return np.dot(X,theta)
def gradient(X,y,theta):
h=hypothesis(X,theta)
grad=np.dot(X.transpose(),(h-y))
return grad
def cost(X,y,theta):
h=hypothesis(X,theta)
J=np.dot((h-y).transpose(),(h-y))
J/=2
return J[0]
def create_mini_batches(X,y,batch_size):
mini_batches=[]
data=np.hstack((X,y))
np.random.shuffle(data)
n_minibatches=data.shape[0]//batch_size
i=0
for i in range(n_minibatches+1):
mini_batch=data[i*batch_size:(i+1)*batch_size,:]
X_mini=mini_batch[:,:-1]
Y_mini=mini_batch[:,-1].reshape((-1,1))
mini_batches.append((X_mini,Y_mini))
if data.shape[0]%batch_size!=0:
mini_batch=data[i*batch_size:data.shape[0]]
X_mini=mini_batch[:,:-1]
Y_mini=mini_batch[:,-1].reshape((-1,1))
mini_batches.append((X_mini,Y_mini))
return mini_batches
def gradientDescent(X,y,learning_rate=0.001,batch_size=32):
theta=np.zeros((X.shape[1],1))
error_list=[]
max_iters=3
for itr in range(max_iters):
mini_batches=create_mini_batches(X,y,batch_size)
for mini_batch in mini_batches:
X_mini,y_mini=mini_batch
theta=theta-learning_rate*gradient(X_mini,y_mini,theta)
error_list.append(cost(X_mini,y_mini,theta))
return theta,error_listPanggil fungsi gradientDescent() untuk mengira parameter model (theta) dan memvisualisasikan perubahan dalam fungsi ralat.
theta,error_list=gradientDescent(X_train,y_train)
print("Bias=",theta[0])
print("Coefficients=",theta[1:])
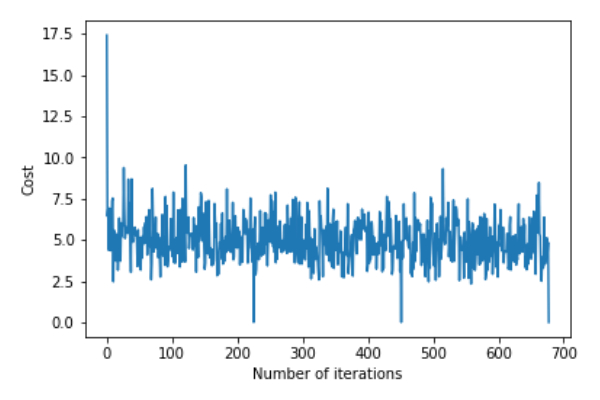
plt.plot(error_list)
plt.xlabel("Number of iterations")
plt.ylabel("Cost")
plt.show()Sisihan=[0.81830471]Koefisien=[[1.04586595]]
Langkah 3: Ramalkan set ujian dan hitung min ralat mutlak dalam ramalan.
y_pred=hypothesis(X_test,theta) plt.scatter(X_test[:,1],y_test[:,],marker='.') plt.plot(X_test[:,1],y_pred,color='orange') plt.show() error=np.sum(np.abs(y_test-y_pred)/y_test.shape[0]) print(& quot Mean absolute error=",error)
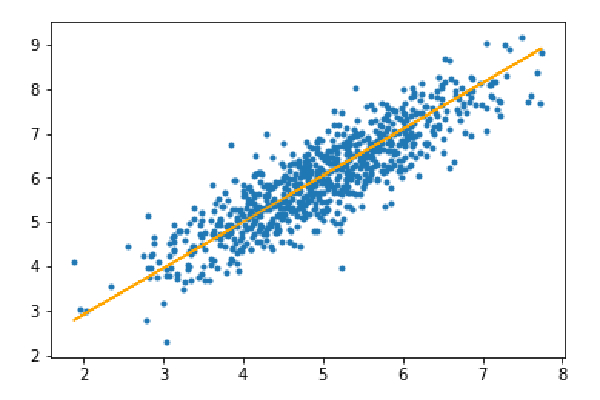
Min ralat mutlak=0.4366644295854125
Garis oren mewakili fungsi hipotesis akhir: theta[0]+theta[1]*X_test[:,1]+theta[2]*X_test[:,2]=0
Atas ialah kandungan terperinci Logik kod untuk melaksanakan algoritma penurunan kecerunan kelompok mini menggunakan Python. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!




