Gunakan Python untuk menulis kod operasi pemadaman pokok B+

Operasi pemadaman pokok B+ memerlukan mencari lokasi nod yang dipadamkan dahulu, dan kemudian menentukan bilangan kekunci nod tersebut.

Jika bilangan kekunci dalam nod melebihi nombor minimum, padamkan sahaja terus.

Seperti yang ditunjukkan di bawah, padamkan "40":

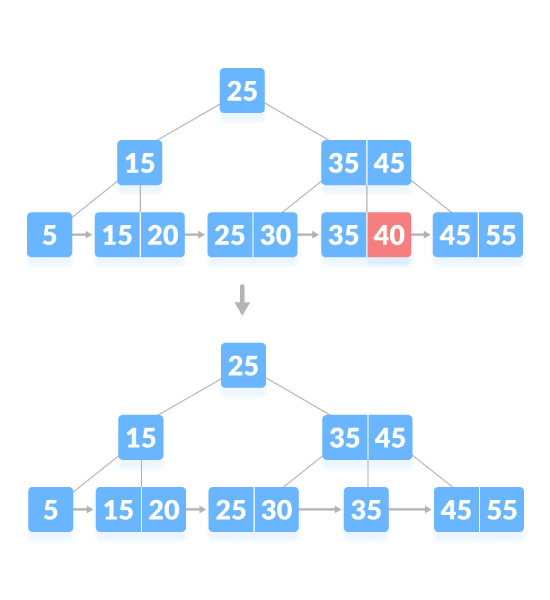
Jika terdapat bilangan kunci minimum yang tepat dalam nod, pemadaman memerlukan peminjaman daripada nod adik-beradik dan menambah kunci perantaraan nod adik-beradik ke nod induk. Seperti yang ditunjukkan di bawah, padamkan "5":

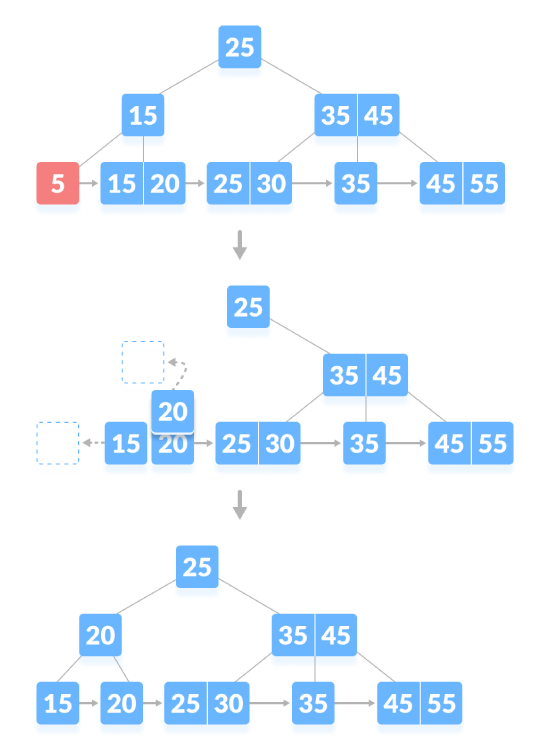
Padamkan nod kandungan, jika bilangan kekunci dalam nod melebihi nombor minimum, hanya padamkan kekunci dari nod daun dan padamkan kekunci dari nod dalaman . Isi ruang kosong dalam nod dalaman dengan pengganti tersusun. Seperti yang ditunjukkan di bawah, padamkan "45":

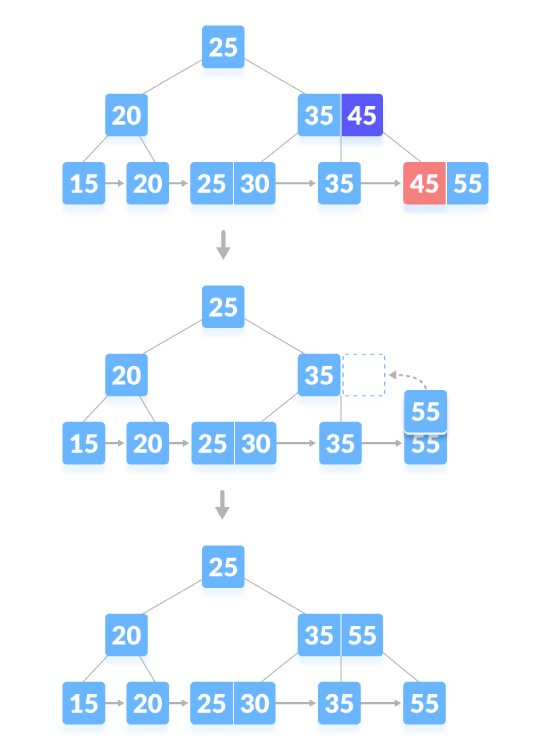
Padamkan nod kandungan, jika terdapat bilangan kekunci minimum yang tepat dalam nod, padamkan kunci dan pinjam kunci terus daripada nod adik-beradik, dan isikan indeks dengan kunci yang dipinjam ruang kosong. Seperti yang ditunjukkan di bawah, padamkan "35":

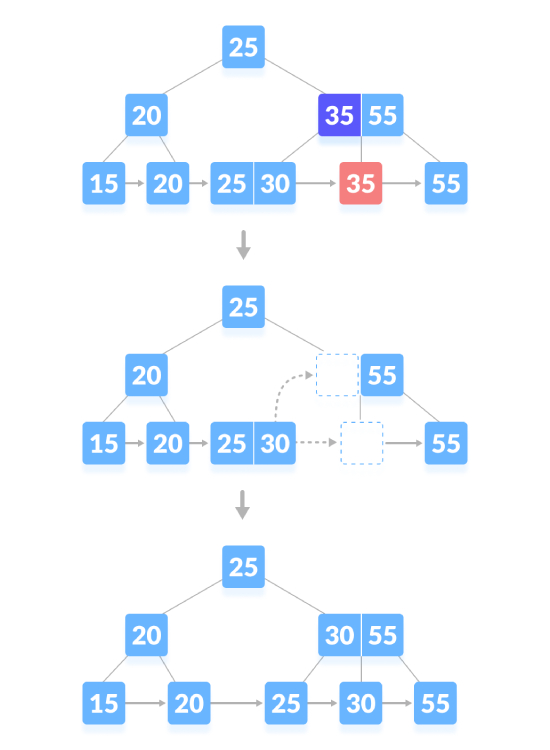
Padamkan nod kandungan dan jana ruang kosong di atas nod induk. Selepas memadamkan kunci, gabungkan ruang kosong dengan adik-beradiknya, mengisi ruang kosong dalam nod induk dengan pengganti tertib. Seperti yang ditunjukkan di bawah, padamkan "25":

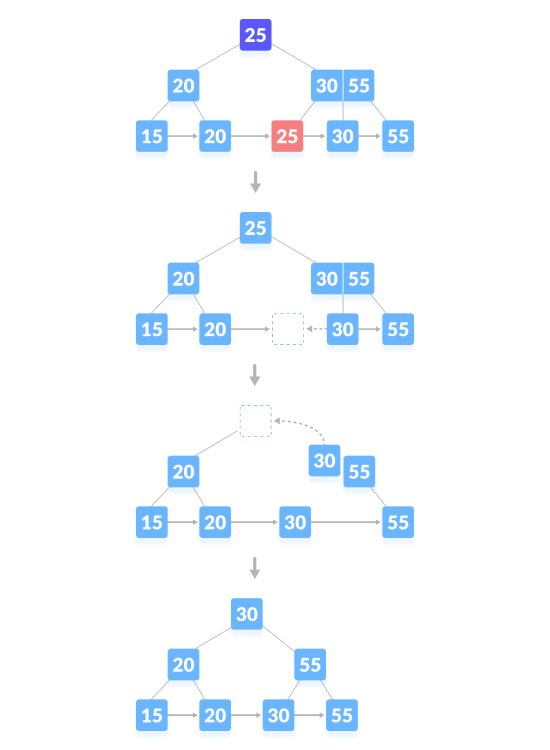
Operasi pemadaman yang menyebabkan ketinggian pokok mengecut, seperti yang ditunjukkan di bawah, padamkan "55":

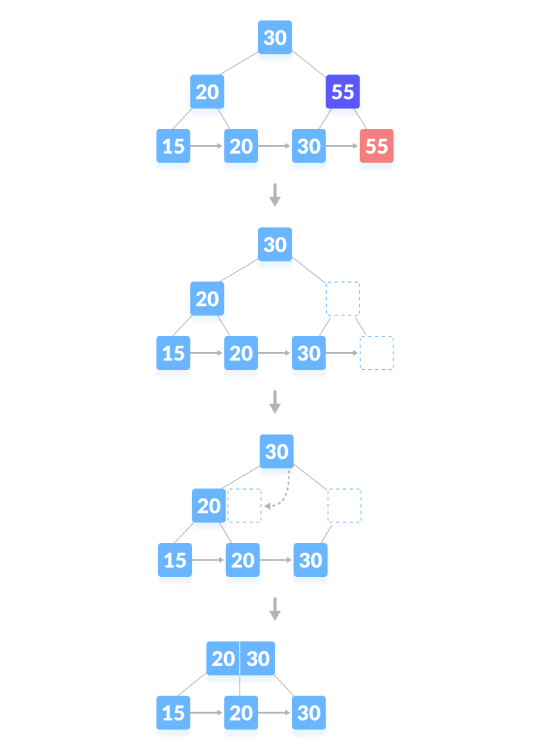
Pelaksanaan operasi seterusnya

import math
# 创建节点
class Node:
    def __init__(self, order):
        self.order = order
        self.values = []
        self.keys = []
        self.nextKey = None
        self.parent = None
        self.check_leaf = False

# 插入叶子
    def insert_at_leaf(self, leaf, value, key):
        if (self.values):
            temp1 = self.values
            for i in range(len(temp1)):
                if (value == temp1[i]):
                    self.keys[i].append(key)
                    break
                elif (value < temp1[i]):
                    self.values = self.values[:i] + [value] + self.values[i:]
                    self.keys = self.keys[:i] + [[key]] + self.keys[i:]
                    break
                elif (i + 1 == len(temp1)):
                    self.values.append(value)
                    self.keys.append([key])
                    break
        else:
            self.values = [value]
            self.keys = [[key]]


# B+树
class BplusTree:
    def __init__(self, order):
        self.root = Node(order)
        self.root.check_leaf = True

    # 插入节点
    def insert(self, value, key):
        value = str(value)
        old_node = self.search(value)
        old_node.insert_at_leaf(old_node, value, key)

        if (len(old_node.values) == old_node.order):
            node1 = Node(old_node.order)
            node1.check_leaf = True
            node1.parent = old_node.parent
            mid = int(math.ceil(old_node.order / 2)) - 1
            node1.values = old_node.values[mid + 1:]
            node1.keys = old_node.keys[mid + 1:]
            node1.nextKey = old_node.nextKey
            old_node.values = old_node.values[:mid + 1]
            old_node.keys = old_node.keys[:mid + 1]
            old_node.nextKey = node1
            self.insert_in_parent(old_node, node1.values[0], node1)

    def search(self, value):
        current_node = self.root
        while(current_node.check_leaf == False):
            temp2 = current_node.values
            for i in range(len(temp2)):
                if (value == temp2[i]):
                    current_node = current_node.keys[i + 1]
                    break
                elif (value < temp2[i]):
                    current_node = current_node.keys[i]
                    break
                elif (i + 1 == len(current_node.values)):
                    current_node = current_node.keys[i + 1]
                    break
        return current_node

    # 查找节点
    def find(self, value, key):
        l = self.search(value)
        for i, item in enumerate(l.values):
            if item == value:
                if key in l.keys[i]:
                    return True
                else:
                    return False
        return False

    # 在父级插入
    def insert_in_parent(self, n, value, ndash):
        if (self.root == n):
            rootNode = Node(n.order)
            rootNode.values = [value]
            rootNode.keys = [n, ndash]
            self.root = rootNode
            n.parent = rootNode
            ndash.parent = rootNode
            return

        parentNode = n.parent
        temp3 = parentNode.keys
        for i in range(len(temp3)):
            if (temp3[i] == n):
                parentNode.values = parentNode.values[:i] + \
                    [value] + parentNode.values[i:]
                parentNode.keys = parentNode.keys[:i +
                                                  1] + [ndash] + parentNode.keys[i + 1:]
                if (len(parentNode.keys) > parentNode.order):
                    parentdash = Node(parentNode.order)
                    parentdash.parent = parentNode.parent
                    mid = int(math.ceil(parentNode.order / 2)) - 1
                    parentdash.values = parentNode.values[mid + 1:]
                    parentdash.keys = parentNode.keys[mid + 1:]
                    value_ = parentNode.values[mid]
                    if (mid == 0):
                        parentNode.values = parentNode.values[:mid + 1]
                    else:
                        parentNode.values = parentNode.values[:mid]
                    parentNode.keys = parentNode.keys[:mid + 1]
                    for j in parentNode.keys:
                        j.parent = parentNode
                    for j in parentdash.keys:
                        j.parent = parentdash
                    self.insert_in_parent(parentNode, value_, parentdash)

    # 删除节点
    def delete(self, value, key):
        node_ = self.search(value)

        temp = 0
        for i, item in enumerate(node_.values):
            if item == value:
                temp = 1

                if key in node_.keys[i]:
                    if len(node_.keys[i]) > 1:
                        node_.keys[i].pop(node_.keys[i].index(key))
                    elif node_ == self.root:
                        node_.values.pop(i)
                        node_.keys.pop(i)
                    else:
                        node_.keys[i].pop(node_.keys[i].index(key))
                        del node_.keys[i]
                        node_.values.pop(node_.values.index(value))
                        self.deleteEntry(node_, value, key)
                else:
                    print("Value not in Key")
                    return
        if temp == 0:
            print("Value not in Tree")
            return

    # 删除条目
    def deleteEntry(self, node_, value, key):

        if not node_.check_leaf:
            for i, item in enumerate(node_.keys):
                if item == key:
                    node_.keys.pop(i)
                    break
            for i, item in enumerate(node_.values):
                if item == value:
                    node_.values.pop(i)
                    break

        if self.root == node_ and len(node_.keys) == 1:
            self.root = node_.keys[0]
            node_.keys[0].parent = None
            del node_
            return
        elif (len(node_.keys) < int(math.ceil(node_.order / 2)) and node_.check_leaf == False) or (len(node_.values) < int(math.ceil((node_.order - 1) / 2)) and node_.check_leaf == True):

            is_predecessor = 0
            parentNode = node_.parent
            PrevNode = -1
            NextNode = -1
            PrevK = -1
            PostK = -1
            for i, item in enumerate(parentNode.keys):

                if item == node_:
                    if i > 0:
                        PrevNode = parentNode.keys[i - 1]
                        PrevK = parentNode.values[i - 1]

                    if i < len(parentNode.keys) - 1:
                        NextNode = parentNode.keys[i + 1]
                        PostK = parentNode.values[i]

            if PrevNode == -1:
                ndash = NextNode
                value_ = PostK
            elif NextNode == -1:
                is_predecessor = 1
                ndash = PrevNode
                value_ = PrevK
            else:
                if len(node_.values) + len(NextNode.values) < node_.order:
                    ndash = NextNode
                    value_ = PostK
                else:
                    is_predecessor = 1
                    ndash = PrevNode
                    value_ = PrevK

            if len(node_.values) + len(ndash.values) < node_.order:
                if is_predecessor == 0:
                    node_, ndash = ndash, node_
                ndash.keys += node_.keys
                if not node_.check_leaf:
                    ndash.values.append(value_)
                else:
                    ndash.nextKey = node_.nextKey
                ndash.values += node_.values

                if not ndash.check_leaf:
                    for j in ndash.keys:
                        j.parent = ndash

                self.deleteEntry(node_.parent, value_, node_)
                del node_
            else:
                if is_predecessor == 1:
                    if not node_.check_leaf:
                        ndashpm = ndash.keys.pop(-1)
                        ndashkm_1 = ndash.values.pop(-1)
                        node_.keys = [ndashpm] + node_.keys
                        node_.values = [value_] + node_.values
                        parentNode = node_.parent
                        for i, item in enumerate(parentNode.values):
                            if item == value_:
                                p.values[i] = ndashkm_1
                                break
                    else:
                        ndashpm = ndash.keys.pop(-1)
                        ndashkm = ndash.values.pop(-1)
                        node_.keys = [ndashpm] + node_.keys
                        node_.values = [ndashkm] + node_.values
                        parentNode = node_.parent
                        for i, item in enumerate(p.values):
                            if item == value_:
                                parentNode.values[i] = ndashkm
                                break
                else:
                    if not node_.check_leaf:
                        ndashp0 = ndash.keys.pop(0)
                        ndashk0 = ndash.values.pop(0)
                        node_.keys = node_.keys + [ndashp0]
                        node_.values = node_.values + [value_]
                        parentNode = node_.parent
                        for i, item in enumerate(parentNode.values):
                            if item == value_:
                                parentNode.values[i] = ndashk0
                                break
                    else:
                        ndashp0 = ndash.keys.pop(0)
                        ndashk0 = ndash.values.pop(0)
                        node_.keys = node_.keys + [ndashp0]
                        node_.values = node_.values + [ndashk0]
                        parentNode = node_.parent
                        for i, item in enumerate(parentNode.values):
                            if item == value_:
                                parentNode.values[i] = ndash.values[0]
                                break

                if not ndash.check_leaf:
                    for j in ndash.keys:
                        j.parent = ndash
                if not node_.check_leaf:
                    for j in node_.keys:
                        j.parent = node_
                if not parentNode.check_leaf:
                    for j in parentNode.keys:
                        j.parent = parentNode


# 输出B+树
def printTree(tree):
    lst = [tree.root]
    level = [0]
    leaf = None
    flag = 0
    lev_leaf = 0

    node1 = Node(str(level[0]) + str(tree.root.values))

    while (len(lst) != 0):
        x = lst.pop(0)
        lev = level.pop(0)
        if (x.check_leaf == False):
            for i, item in enumerate(x.keys):
                print(item.values)
        else:
            for i, item in enumerate(x.keys):
                print(item.values)
            if (flag == 0):
                lev_leaf = lev
                leaf = x
                flag = 1

record_len = 3
bplustree = BplusTree(record_len)
bplustree.insert(&#x27;5&#x27;, &#x27;33&#x27;)
bplustree.insert(&#x27;15&#x27;, &#x27;21&#x27;)
bplustree.insert(&#x27;25&#x27;, &#x27;31&#x27;)
bplustree.insert(&#x27;35&#x27;, &#x27;41&#x27;)
bplustree.insert(&#x27;45&#x27;, &#x27;10&#x27;)

printTree(bplustree)

if(bplustree.find(&#x27;5&#x27;, &#x27;34&#x27;)):
    print("Found")
else:
    print("Not found")

Atas ialah kandungan terperinci Gunakan Python untuk menulis kod operasi pemadaman pokok B+. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!