 pembangunan bahagian belakang
pembangunan bahagian belakang
 Tutorial Python
Tutorial Python
 Menghuraikan algoritma Ford-Fulkerson dan melaksanakannya melalui Python
Menghuraikan algoritma Ford-Fulkerson dan melaksanakannya melalui Python
Menghuraikan algoritma Ford-Fulkerson dan melaksanakannya melalui Python
Algoritma Ford-Fulkerson ialah algoritma tamak yang digunakan untuk mengira trafik maksimum dalam rangkaian. Prinsipnya adalah untuk mencari laluan penambahan dengan kapasiti baki positif Selagi laluan penambahan ditemui, anda boleh terus menambah laluan dan mengira trafik. Sehingga laluan penambahan tidak lagi wujud, kadar aliran maksimum boleh diperolehi.
Terminologi algoritma Ford-Fulkerson
Baki kapasiti: Ia adalah kapasiti tolak aliran Dalam algoritma Ford-Fulkerson, baki kapasiti ialah nombor positif sebelum ia boleh terus menjadi laluan.
Rangkaian sisa: Ia adalah rangkaian dengan bucu dan tepi yang sama, menggunakan kapasiti baki sebagai kapasiti.
Laluan tambahan: Ia ialah laluan dari titik sumber ke titik penerimaan dalam graf baki, dengan kapasiti akhir 0.
Contoh prinsip algoritma Ford-Fulkerson
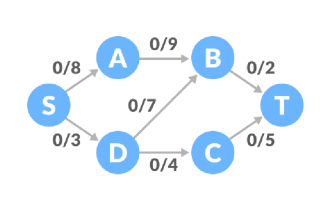
Konsepnya mungkin tidak begitu jelas Mari kita lihat contoh Trafik awal semua tepi rangkaian aliran ialah 0, dan terdapat had kapasiti atas yang sepadan menjadi S dan titik penerimaan ialah T. .
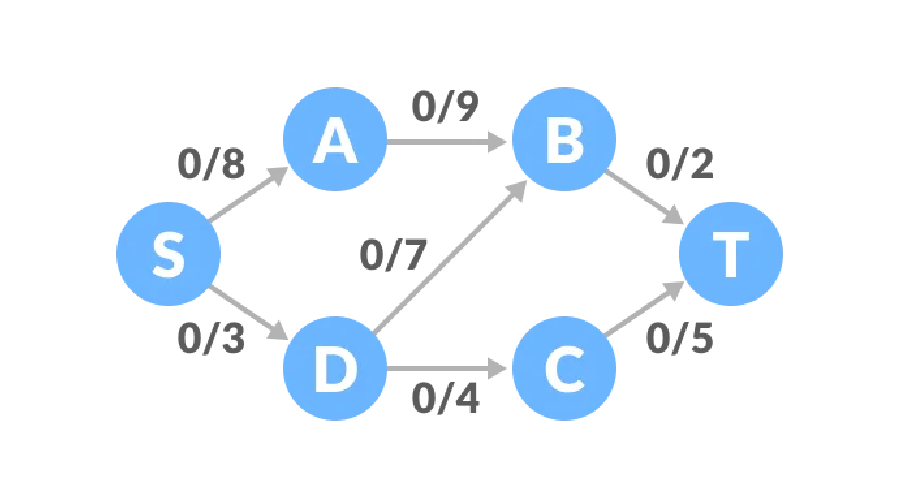
Laluan satu, baki kapasiti laluan S-A-B-T ialah 8, 9, 2, dan nilai minimum ialah 2, jadi trafik laluan satu ialah 2, dan trafik rajah rangkaian ialah 2.
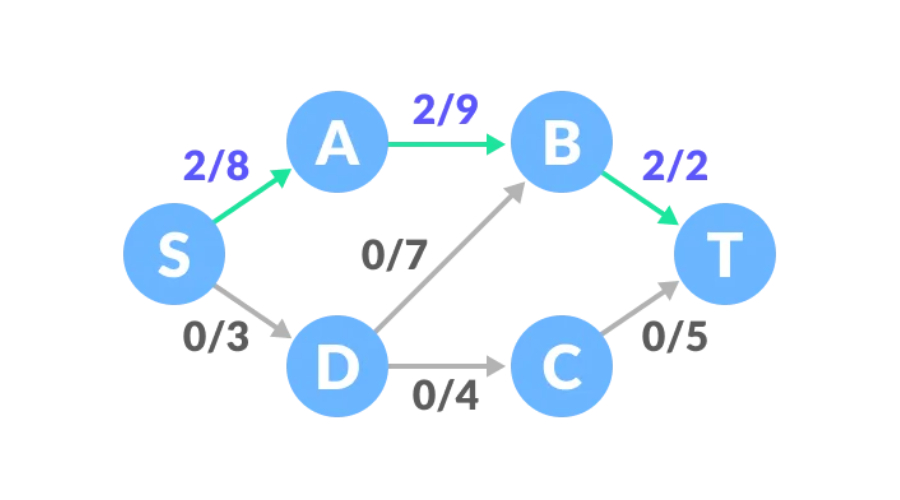
Laluan dua, baki kapasiti laluan S-D-C-T ialah 3, 4, 5, dan nilai minimum ialah 3, jadi kita boleh meningkatkan trafik sebanyak 3, dan trafik rangkaian ialah 5.
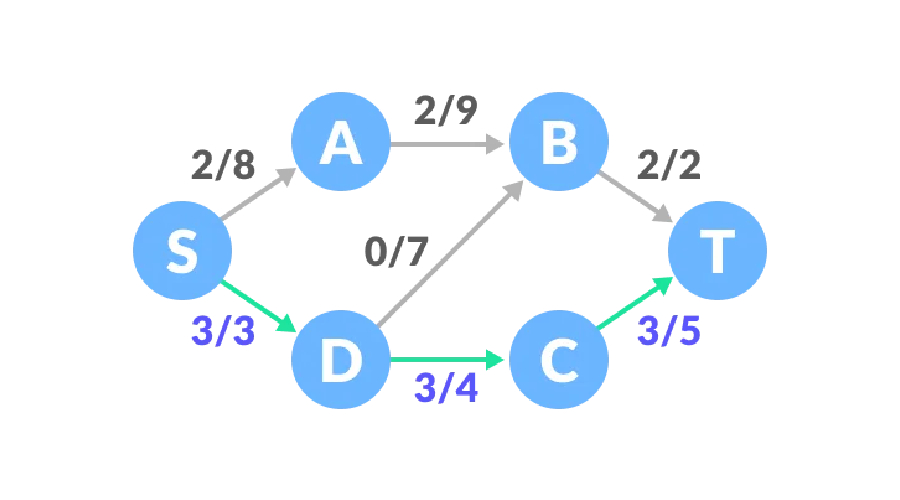
Laluan tiga, baki kapasiti laluan S-A-B-D-C-T ialah 6, 7, 7, 1, 2, dan nilai minimum ialah 1, jadi trafik meningkat sebanyak 1, dan trafik rangkaian ialah 6.
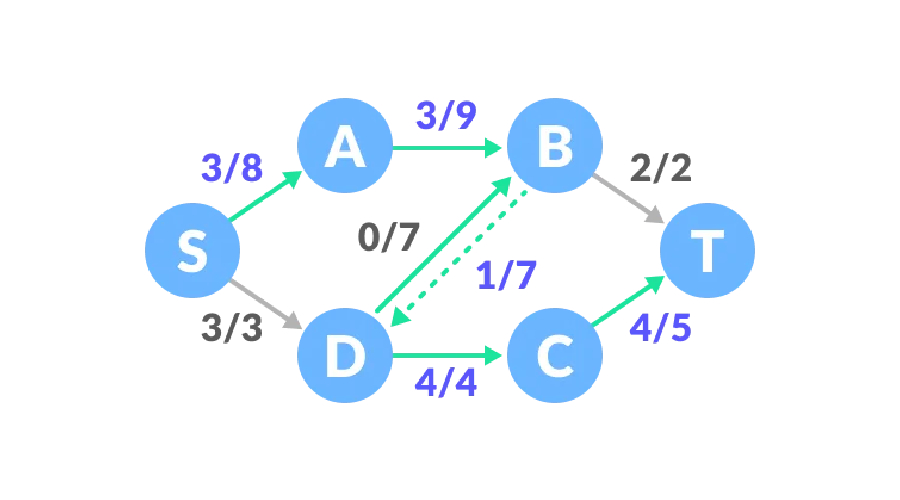
Pada ketika ini, tiada kapasiti baki positif, dan aliran maksimum rangkaian aliran ini ialah 6.
Python melaksanakan algoritma Ford-Fulkerson
from collections import defaultdict
class Graph:
def __init__(self, graph):
self.graph = graph
self. ROW = len(graph)
def searching_algo_BFS(self, s, t, parent):
visited = [False] * (self.ROW)
queue = []
queue.append(s)
visited[s] = True
while queue:
u = queue.pop(0)
for ind, val in enumerate(self.graph[u]):
if visited[ind] == False and val > 0:
queue.append(ind)
visited[ind] = True
parent[ind] = u
return True if visited[t] else False
def ford_fulkerson(self, source, sink):
parent = [-1] * (self.ROW)
max_flow = 0
while self.searching_algo_BFS(source, sink, parent):
path_flow = float("Inf")
s = sink
while(s != source):
path_flow = min(path_flow, self.graph[parent[s]][s])
s = parent[s]
max_flow += path_flow
v = sink
while(v != source):
u = parent[v]
self.graph[u][v] -= path_flow
self.graph[v][u] += path_flow
v = parent[v]
return max_flow
graph = [[0, 8, 0, 0, 3, 0],
[0, 0, 9, 0, 0, 0],
[0, 0, 0, 0, 7, 2],
[0, 0, 0, 0, 0, 5],
[0, 0, 7, 4, 0, 0],
[0, 0, 0, 0, 0, 0]]
g = Graph(graph)
source = 0
sink = 5
print("Max Flow: %d " % g.ford_fulkerson(source, sink))Atas ialah kandungan terperinci Menghuraikan algoritma Ford-Fulkerson dan melaksanakannya melalui Python. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

AI Hentai Generator
Menjana ai hentai secara percuma.

Artikel Panas

Alat panas

Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma

SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan

Hantar Studio 13.0.1
Persekitaran pembangunan bersepadu PHP yang berkuasa

Dreamweaver CS6
Alat pembangunan web visual

SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)

Topik panas
 1378
1378
 52
52
 Bagaimana untuk melaksanakan algoritma tamak dalam C#
Sep 19, 2023 am 11:48 AM
Bagaimana untuk melaksanakan algoritma tamak dalam C#
Sep 19, 2023 am 11:48 AM
Bagaimana untuk melaksanakan algoritma tamak dalam C# Algoritma tamak (Algoritma tamak) ialah kaedah penyelesaian masalah yang biasa digunakan Ia memilih penyelesaian optimum semasa setiap kali dengan harapan untuk mendapatkan penyelesaian optimum global. Dalam C#, kita boleh menggunakan algoritma tamak untuk menyelesaikan banyak masalah praktikal. Artikel ini akan memperkenalkan cara melaksanakan algoritma tamak dalam C# dan memberikan contoh kod khusus. 1. Prinsip asas algoritma tamak Idea asas algoritma tamak adalah untuk memilih penyelesaian optimum semasa setiap kali, tanpa mengira kemungkinan kesan daripada langkah-langkah berikutnya. Pemikiran begini
 Bagaimana untuk melaksanakan penyelesaian yang cekap kepada masalah perubahan syiling paling sedikit dalam PHP menggunakan algoritma tamak?
Sep 19, 2023 am 10:22 AM
Bagaimana untuk melaksanakan penyelesaian yang cekap kepada masalah perubahan syiling paling sedikit dalam PHP menggunakan algoritma tamak?
Sep 19, 2023 am 10:22 AM
Bagaimana untuk melaksanakan penyelesaian yang cekap kepada masalah perubahan syiling paling sedikit dalam PHP menggunakan algoritma tamak? Pendahuluan: Dalam kehidupan seharian, kita selalunya perlu melakukan perubahan, terutamanya ketika berbelanja atau berdagang. Untuk menggunakan seberapa sedikit syiling yang mungkin, amaun perubahan harus digabungkan menggunakan seberapa sedikit syiling yang mungkin. Dalam pengaturcaraan komputer, kita boleh menggunakan algoritma tamak untuk menyelesaikan masalah ini untuk mendapatkan penyelesaian yang cekap. Artikel ini akan memperkenalkan cara menggunakan algoritma tamak dalam PHP untuk mencapai penyelesaian yang cekap kepada masalah perubahan syiling minimum, dan memberikan contoh kod yang sepadan.
 Menghuraikan algoritma Ford-Fulkerson dan melaksanakannya melalui Python
Jan 22, 2024 pm 08:09 PM
Menghuraikan algoritma Ford-Fulkerson dan melaksanakannya melalui Python
Jan 22, 2024 pm 08:09 PM
Algoritma Ford-Fulkerson ialah algoritma tamak yang digunakan untuk mengira kadar aliran maksimum dalam rangkaian. Prinsipnya adalah untuk mencari laluan penambahan dengan kapasiti baki positif Selagi laluan penambahan ditemui, anda boleh terus menambah laluan dan mengira trafik. Sehingga laluan penambahan tidak lagi wujud, kadar aliran maksimum boleh diperolehi. Istilah baki kapasiti algoritma Ford-Fulkerson adalah untuk menolak aliran daripada kapasiti Dalam algoritma Ford-Fulkerson, kapasiti baki adalah nombor positif sebelum ia boleh terus digunakan sebagai laluan. Rangkaian sisa: Ia adalah rangkaian dengan bucu dan tepi yang sama, menggunakan kapasiti baki sebagai kapasiti. Laluan tambahan: Ia ialah laluan dari titik sumber ke titik penerimaan dalam graf baki, dengan kapasiti akhir 0. Garis besar contoh prinsip algoritma Ford-Fulkerson yang mungkin
 Bagaimana untuk melaksanakan algoritma tamak menggunakan Python?
Sep 19, 2023 am 11:43 AM
Bagaimana untuk melaksanakan algoritma tamak menggunakan Python?
Sep 19, 2023 am 11:43 AM
Bagaimana untuk melaksanakan algoritma tamak menggunakan Python? Algoritma Greedy ialah algoritma mudah dan berkesan yang sesuai untuk menyelesaikan masalah dengan sifat substruktur yang optimum. Ia memerlukan pilihan terbaik dalam keadaan semasa dalam setiap langkah pemilihan, dengan harapan untuk mencari penyelesaian optimum global. Dalam artikel ini, kami akan memperkenalkan cara menggunakan Python untuk melaksanakan algoritma tamak, dengan contoh kod khusus. 1. Idea asas algoritma tamak Idea asas algoritma tamak adalah untuk memilih penyelesaian optimum dalam keadaan semasa pada setiap langkah, dan kemudian
 Bagaimana untuk menulis algoritma tamak menggunakan PHP
Jul 07, 2023 pm 03:45 PM
Bagaimana untuk menulis algoritma tamak menggunakan PHP
Jul 07, 2023 pm 03:45 PM
Cara menggunakan PHP untuk menulis algoritma tamak Algoritma tamak (Algoritma tamak) ialah algoritma yang mudah dan berkesan digunakan untuk menyelesaikan sejenis masalah pengoptimuman. Idea asasnya adalah untuk membuat pilihan pada setiap langkah yang kelihatan terbaik pada masa ini, tanpa mengambil kira akibat masa depan. Artikel ini akan memperkenalkan cara menulis algoritma tamak menggunakan PHP dan memberikan contoh kod yang berkaitan. 1. Huraian Masalah Sebelum menerangkan algoritma tamak, mari kita tentukan dahulu masalah khusus untuk pemahaman yang lebih baik. Katakan ada satu set tugas, setiap tugas ada permulaan
 Algoritma tamak dan pelaksanaannya dalam C++
Aug 22, 2023 am 10:04 AM
Algoritma tamak dan pelaksanaannya dalam C++
Aug 22, 2023 am 10:04 AM
Algoritma tamak ialah idea algoritma yang biasa digunakan dan digunakan secara meluas dalam banyak masalah. Idea teras adalah untuk hanya mempertimbangkan penyelesaian optimum segera apabila membuat keputusan pada setiap langkah, tanpa mengambil kira kesan jangka panjang. Dalam C++, pelaksanaan algoritma tamak selalunya melibatkan operasi asas seperti pengisihan dan pemprosesan data. Di bawah, kami akan memperkenalkan idea algoritma tamak dan pelaksanaannya dalam C++ untuk beberapa masalah biasa. 1. Masalah Penjadualan Aktiviti Memandangkan satu set aktiviti, setiap aktiviti mempunyai masa mula dan masa tamat, dan seseorang hanya boleh mengambil bahagian dalam satu aktiviti pada satu masa.
 Bagaimana untuk melaksanakan algoritma tamak menggunakan java
Sep 19, 2023 am 11:13 AM
Bagaimana untuk melaksanakan algoritma tamak menggunakan java
Sep 19, 2023 am 11:13 AM
Cara menggunakan Java untuk melaksanakan algoritma tamak Algoritma tamak (GreedyAlgorithm) ialah idea algoritma untuk menyelesaikan masalah Ciri-cirinya adalah untuk memilih penyelesaian optimum semasa pada setiap langkah, dengan harapan akhirnya mencapai penyelesaian optimum global melalui setiap penyelesaian optimum tempatan. Ciri mudah dan cekap algoritma tamak menjadikannya algoritma yang biasa digunakan apabila menyelesaikan beberapa masalah pengoptimuman atau masalah khusus tertentu. Artikel ini akan memperkenalkan cara melaksanakan algoritma tamak menggunakan Java dan memberikan contoh kod khusus. 1. Idea asas algoritma tamak Asas algoritma tamak
 Program C/C++ untuk algoritma tamak untuk mencari bilangan minimum syiling
Sep 19, 2023 pm 11:01 PM
Program C/C++ untuk algoritma tamak untuk mencari bilangan minimum syiling
Sep 19, 2023 pm 11:01 PM
Algoritma tamak adalah algoritma yang digunakan untuk mencari penyelesaian optimum kepada masalah tertentu. Algoritma tamak berfungsi dengan mencari penyelesaian optimum tempatan untuk setiap bahagian (penyelesaian optimum untuk satu bahagian masalah), dengan itu menunjukkan bahawa penyelesaian optimum global boleh ditemui. Dalam masalah ini, kami akan menggunakan algoritma Algoritma Greedy untuk mencari bilangan minimum syiling/nota yang boleh membentuk jumlah tertentu. Untuk ini, kami akan mempertimbangkan semua syiling atau wang kertas yang sah, iaitu denominasi {1,2,5,10,20,50,100,200,500,2000}. Kita perlu mengembalikan bilangan syiling/nota yang diperlukan untuk menjumlahkan jumlah tersebut. Mari kita ambil beberapa contoh untuk memahami konteks dengan lebih baik - Contoh 1 - Input: 1231 Output: 7 Penerangan - Kami memerlukan dua nota 500 rupee



