 Peranti teknologi
Peranti teknologi
 AI
AI
 Bandingkan persamaan, perbezaan dan hubungan antara lilitan diluaskan dan lilitan atrus
Bandingkan persamaan, perbezaan dan hubungan antara lilitan diluaskan dan lilitan atrus
Bandingkan persamaan, perbezaan dan hubungan antara lilitan diluaskan dan lilitan atrus

Konvolusi diluaskan dan lilitan diluaskan adalah operasi yang biasa digunakan dalam rangkaian neural konvolusi Artikel ini akan memperkenalkan perbezaan dan hubungannya secara terperinci.
1. Konvolusi diluaskan
Konvolusi diluaskan, juga dikenali sebagai lilitan diluaskan atau lilitan diluaskan, ialah operasi dalam rangkaian saraf konvolusi. Ia adalah lanjutan berdasarkan operasi lilitan tradisional dan meningkatkan medan penerimaan kernel lilitan dengan memasukkan lubang dalam kernel lilitan. Dengan cara ini, rangkaian boleh menangkap lebih banyak ciri yang lebih luas. Konvolusi dilatasi digunakan secara meluas dalam bidang pemprosesan imej dan boleh meningkatkan prestasi rangkaian tanpa menambah bilangan parameter dan jumlah pengiraan. Dengan meluaskan medan penerimaan kernel lilitan, lilitan diluaskan boleh memproses maklumat global dalam imej dengan lebih baik, sekali gus meningkatkan kesan pengekstrakan ciri.
Idea utama konvolusi diluaskan adalah untuk memperkenalkan beberapa selang di sekitar kernel lilitan Selang ini membolehkan kernel lilitan bergerak pada peta ciri input secara "melompat", dengan itu meningkatkan saiz ciri keluaran. map. , sambil mengekalkan saiz kernel lilitan tidak berubah. Secara khusus, dengan mengandaikan bahawa peta ciri input ialah X_{(i+mtimes r),(j+ntimes r)}K_{m,n}
di mana r ialah kadar pengembangan, menunjukkan saiz lubang dalam kernel lilitan, m dan n ialah indeks Baris dan lajur. Dengan menukar saiz kadar pengembangan r, peta ciri medan penerimaan yang berbeza boleh diperolehi.
2. Atrous convolution
Atrous convolution ialah operasi convolution yang biasa digunakan dalam rangkaian neural convolutional Ia sangat serupa dengan konsep convolutional dilated, tetapi ia berbeza sedikit dalam pelaksanaannya. Perbezaan antara lilitan diluaskan dan operasi lilitan tradisional ialah beberapa lubang dimasukkan dalam operasi lilitan ini boleh membuatkan kernel lilitan "melompat" bergerak pada peta ciri input, dengan itu mengurangkan saiz peta ciri keluaran saiz isirong lilitan tidak berubah.
Idea utama konvolusi diluaskan adalah untuk memasukkan beberapa lubang dalam kernel lilitan ini boleh membuat kernel lilitan "melompat" pada peta ciri input, dengan itu meningkatkan saiz peta ciri keluaran mengekalkan saiz kernel lilitan tidak berubah. Secara khusus, dengan mengandaikan bahawa peta ciri input ialah X_{(i+mtimes r),(j+ntimes r)}K_{m,n}
di mana r ialah kadar lubang, menunjukkan saiz lubang yang dimasukkan, m dan n ialah baris dan lajur dalam indeks kernel lilitan. Dengan menukar saiz kadar lubang r, peta ciri medan penerimaan yang berbeza boleh diperolehi.
3. Hubungan antara lilitan diluaskan dan lilitan diluaskan
Konsep lilitan diluaskan dan lilitan diluaskan adalah sangat serupa. Malah, lilitan diluaskan boleh dianggap sebagai bentuk khas lilitan diluaskan, kerana kadar lubang d dalam lilitan diluaskan sebenarnya adalah kadar lubang r-1 dalam lilitan diluaskan. Oleh itu, lilitan diluaskan boleh dianggap sebagai jenis lilitan diluaskan khas, yang mengembangkan medan penerimaan isirong lilitan dengan memasukkan lubang, dan juga boleh dilaksanakan menggunakan lilitan diluaskan.
Selain itu, kedua-dua lilitan diluaskan dan lilitan diluaskan boleh digunakan untuk pelbagai tugas dalam rangkaian saraf konvolusi, seperti pengelasan imej, pembahagian semantik, dsb. Mereka boleh meningkatkan prestasi rangkaian saraf konvolusi dalam tugas yang berbeza . Walau bagaimanapun, oleh kerana kadar lubang d dalam lilitan diluaskan adalah diskret, medan penerimaannya adalah kurang tepat sedikit berbanding lilitan diluaskan. Oleh itu, belitan diluaskan mungkin lebih biasa digunakan dalam tugasan yang memerlukan peningkatan medan penerimaan.
Ringkasnya, lilitan diluaskan dan lilitan diluaskan biasanya digunakan dalam rangkaian neural konvolusi Mereka boleh ditukar kepada satu sama lain dan juga boleh digunakan dalam tugasan yang berbeza Operasi lilitan khusus yang akan digunakan bergantung pada spesifik yang ditentukan mengikut keperluan tugas.
Atas ialah kandungan terperinci Bandingkan persamaan, perbezaan dan hubungan antara lilitan diluaskan dan lilitan atrus. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

Video Face Swap
Tukar muka dalam mana-mana video dengan mudah menggunakan alat tukar muka AI percuma kami!

Artikel Panas

Alat panas

Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma

SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan

Hantar Studio 13.0.1
Persekitaran pembangunan bersepadu PHP yang berkuasa

Dreamweaver CS6
Alat pembangunan web visual

SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)

Topik panas
 1659
1659
 14
14
 1416
1416
 52
52
 1310
1310
 25
25
 1259
1259
 29
29
 1233
1233
 24
24
 Kajian kes menggunakan model LSTM dwiarah untuk pengelasan teks
Jan 24, 2024 am 10:36 AM
Kajian kes menggunakan model LSTM dwiarah untuk pengelasan teks
Jan 24, 2024 am 10:36 AM
Model LSTM dwiarah ialah rangkaian saraf yang digunakan untuk pengelasan teks. Berikut ialah contoh mudah yang menunjukkan cara menggunakan LSTM dwiarah untuk tugasan pengelasan teks. Pertama, kita perlu mengimport perpustakaan dan modul yang diperlukan: importosimportnumpyasnpfromkeras.preprocessing.textimportTokenizerfromkeras.preprocessing.sequenceimportpad_sequencesfromkeras.modelsimportSequentialfromkeras.layersimportDense,Em
 Mengira operan titik terapung (FLOPS) untuk rangkaian saraf
Jan 22, 2024 pm 07:21 PM
Mengira operan titik terapung (FLOPS) untuk rangkaian saraf
Jan 22, 2024 pm 07:21 PM
FLOPS ialah salah satu piawaian untuk penilaian prestasi komputer, digunakan untuk mengukur bilangan operasi titik terapung sesaat. Dalam rangkaian saraf, FLOPS sering digunakan untuk menilai kerumitan pengiraan model dan penggunaan sumber pengkomputeran. Ia adalah penunjuk penting yang digunakan untuk mengukur kuasa pengkomputeran dan kecekapan komputer. Rangkaian saraf ialah model kompleks yang terdiri daripada berbilang lapisan neuron yang digunakan untuk tugas seperti klasifikasi data, regresi dan pengelompokan. Latihan dan inferens rangkaian saraf memerlukan sejumlah besar pendaraban matriks, konvolusi dan operasi pengiraan lain, jadi kerumitan pengiraan adalah sangat tinggi. FLOPS (FloatingPointOperationsperSecond) boleh digunakan untuk mengukur kerumitan pengiraan rangkaian saraf untuk menilai kecekapan penggunaan sumber pengiraan model. FLOP
 Terokai konsep, perbezaan, kebaikan dan keburukan RNN, LSTM dan GRU
Jan 22, 2024 pm 07:51 PM
Terokai konsep, perbezaan, kebaikan dan keburukan RNN, LSTM dan GRU
Jan 22, 2024 pm 07:51 PM
Dalam data siri masa, terdapat kebergantungan antara pemerhatian, jadi ia tidak bebas antara satu sama lain. Walau bagaimanapun, rangkaian saraf tradisional menganggap setiap pemerhatian sebagai bebas, yang mengehadkan keupayaan model untuk memodelkan data siri masa. Untuk menyelesaikan masalah ini, Rangkaian Neural Berulang (RNN) telah diperkenalkan, yang memperkenalkan konsep ingatan untuk menangkap ciri dinamik data siri masa dengan mewujudkan kebergantungan antara titik data dalam rangkaian. Melalui sambungan berulang, RNN boleh menghantar maklumat sebelumnya ke dalam pemerhatian semasa untuk meramalkan nilai masa hadapan dengan lebih baik. Ini menjadikan RNN alat yang berkuasa untuk tugasan yang melibatkan data siri masa. Tetapi bagaimanakah RNN mencapai ingatan seperti ini? RNN merealisasikan ingatan melalui gelung maklum balas dalam rangkaian saraf Ini adalah perbezaan antara RNN dan rangkaian saraf tradisional.
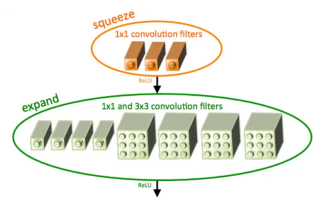 Pengenalan kepada SqueezeNet dan ciri-cirinya
Jan 22, 2024 pm 07:15 PM
Pengenalan kepada SqueezeNet dan ciri-cirinya
Jan 22, 2024 pm 07:15 PM
SqueezeNet ialah algoritma kecil dan tepat yang memberikan keseimbangan yang baik antara ketepatan tinggi dan kerumitan rendah, menjadikannya sesuai untuk sistem mudah alih dan terbenam dengan sumber terhad. Pada 2016, penyelidik dari DeepScale, University of California, Berkeley, dan Stanford University mencadangkan SqueezeNet, rangkaian neural convolutional (CNN) yang padat dan cekap. Dalam beberapa tahun kebelakangan ini, penyelidik telah membuat beberapa penambahbaikan pada SqueezeNet, termasuk SqueezeNetv1.1 dan SqueezeNetv2.0. Penambahbaikan dalam kedua-dua versi bukan sahaja meningkatkan ketepatan tetapi juga mengurangkan kos pengiraan. Ketepatan SqueezeNetv1.1 pada dataset ImageNet
 Bandingkan persamaan, perbezaan dan hubungan antara lilitan diluaskan dan lilitan atrus
Jan 22, 2024 pm 10:27 PM
Bandingkan persamaan, perbezaan dan hubungan antara lilitan diluaskan dan lilitan atrus
Jan 22, 2024 pm 10:27 PM
Konvolusi diluaskan dan lilitan diluaskan adalah operasi yang biasa digunakan dalam rangkaian neural konvolusi Artikel ini akan memperkenalkan perbezaan dan hubungannya secara terperinci. 1. Konvolusi diluaskan Konvolusi diluaskan, juga dikenali sebagai lilitan diluaskan atau lilitan diluaskan, ialah operasi dalam rangkaian neural konvolusi. Ia adalah lanjutan berdasarkan operasi lilitan tradisional dan meningkatkan medan penerimaan kernel lilitan dengan memasukkan lubang dalam kernel lilitan. Dengan cara ini, rangkaian boleh menangkap lebih banyak ciri yang lebih luas. Konvolusi dilatasi digunakan secara meluas dalam bidang pemprosesan imej dan boleh meningkatkan prestasi rangkaian tanpa menambah bilangan parameter dan jumlah pengiraan. Dengan meluaskan medan penerimaan kernel lilitan, lilitan diluaskan boleh memproses maklumat global dalam imej dengan lebih baik, sekali gus meningkatkan kesan pengekstrakan ciri. Idea utama lilitan diluaskan adalah untuk memperkenalkan beberapa
 Rangkaian Neural Berkembar: Analisis Prinsip dan Aplikasi
Jan 24, 2024 pm 04:18 PM
Rangkaian Neural Berkembar: Analisis Prinsip dan Aplikasi
Jan 24, 2024 pm 04:18 PM
Rangkaian Neural Siam ialah struktur rangkaian saraf tiruan yang unik. Ia terdiri daripada dua rangkaian neural yang sama yang berkongsi parameter dan berat yang sama. Pada masa yang sama, kedua-dua rangkaian juga berkongsi data input yang sama. Reka bentuk ini diilhamkan oleh kembar, kerana kedua-dua rangkaian saraf adalah sama dari segi struktur. Prinsip rangkaian saraf Siam adalah untuk menyelesaikan tugas tertentu, seperti padanan imej, padanan teks dan pengecaman muka, dengan membandingkan persamaan atau jarak antara dua data input. Semasa latihan, rangkaian cuba untuk memetakan data yang serupa ke wilayah bersebelahan dan data yang tidak serupa ke wilayah yang jauh. Dengan cara ini, rangkaian boleh belajar cara mengklasifikasikan atau memadankan data yang berbeza dan mencapai yang sepadan
 rangkaian neural convolutional sebab
Jan 24, 2024 pm 12:42 PM
rangkaian neural convolutional sebab
Jan 24, 2024 pm 12:42 PM
Rangkaian neural convolutional kausal ialah rangkaian neural convolutional khas yang direka untuk masalah kausalitas dalam data siri masa. Berbanding dengan rangkaian neural convolutional konvensional, rangkaian neural convolutional kausal mempunyai kelebihan unik dalam mengekalkan hubungan kausal siri masa dan digunakan secara meluas dalam ramalan dan analisis data siri masa. Idea teras rangkaian neural convolutional kausal adalah untuk memperkenalkan kausalitas dalam operasi konvolusi. Rangkaian saraf konvolusional tradisional boleh melihat data secara serentak sebelum dan selepas titik masa semasa, tetapi dalam ramalan siri masa, ini mungkin membawa kepada masalah kebocoran maklumat. Kerana keputusan ramalan pada titik masa semasa akan dipengaruhi oleh data pada titik masa akan datang. Rangkaian saraf konvolusi penyebab menyelesaikan masalah ini Ia hanya dapat melihat titik masa semasa dan data sebelumnya, tetapi tidak dapat melihat data masa depan.
 Penghapusan imej menggunakan rangkaian saraf konvolusi
Jan 23, 2024 pm 11:48 PM
Penghapusan imej menggunakan rangkaian saraf konvolusi
Jan 23, 2024 pm 11:48 PM
Rangkaian neural konvolusi berfungsi dengan baik dalam tugasan menghilangkan imej. Ia menggunakan penapis yang dipelajari untuk menapis bunyi dan dengan itu memulihkan imej asal. Artikel ini memperkenalkan secara terperinci kaedah denoising imej berdasarkan rangkaian neural convolutional. 1. Gambaran Keseluruhan Rangkaian Neural Konvolusi Rangkaian saraf konvolusi ialah algoritma pembelajaran mendalam yang menggunakan gabungan berbilang lapisan konvolusi, lapisan gabungan dan lapisan bersambung sepenuhnya untuk mempelajari dan mengelaskan ciri imej. Dalam lapisan konvolusi, ciri tempatan imej diekstrak melalui operasi konvolusi, dengan itu menangkap korelasi spatial dalam imej. Lapisan pengumpulan mengurangkan jumlah pengiraan dengan mengurangkan dimensi ciri dan mengekalkan ciri utama. Lapisan bersambung sepenuhnya bertanggungjawab untuk memetakan ciri dan label yang dipelajari untuk melaksanakan pengelasan imej atau tugas lain. Reka bentuk struktur rangkaian ini menjadikan rangkaian neural konvolusi berguna dalam pemprosesan dan pengecaman imej.



