Pengenalan kepada rangkaian saraf yang didorong oleh maklumat fizikal

Rangkaian Neural Berasaskan Maklumat Fizik (PINN) ialah kaedah yang menggabungkan model fizikal dan rangkaian saraf. Dengan menyepadukan kaedah fizikal ke dalam rangkaian saraf, PINN boleh mempelajari tingkah laku dinamik sistem tak linear. Berbanding dengan kaedah berasaskan model fizikal tradisional, PINN mempunyai fleksibiliti dan skalabiliti yang lebih tinggi. Ia secara adaptif boleh mempelajari sistem dinamik tak linear yang kompleks sambil memenuhi keperluan spesifikasi fizikal. Artikel ini akan memperkenalkan prinsip asas PINN dan menyediakan beberapa contoh aplikasi praktikal.
Prinsip asas PINN adalah untuk menyepadukan kaedah fizikal ke dalam rangkaian saraf untuk mempelajari tingkah laku dinamik sistem. Secara khusus, kita boleh menyatakan kaedah fizikal sebagai bentuk berikut:
F(u(x),frac{partial u}{partial x},x,t)=0
Matlamat kami adalah untuk lulus Belajar evolusi masa perubahan keadaan sistem u(x) dan keadaan sempadan di sekeliling sistem untuk memahami kelakuan sistem. Untuk mencapai matlamat ini, kita boleh menggunakan rangkaian saraf untuk mensimulasikan pembangunan perubahan keadaan u(x) dan menggunakan teknik pembezaan automatik untuk mengira kecerunan perubahan keadaan. Pada masa yang sama, kita juga boleh menggunakan kaedah fizikal untuk mengekang hubungan antara rangkaian saraf dan perubahan keadaan. Dengan cara ini, kita boleh lebih memahami evolusi keadaan sistem dan meramalkan perubahan masa hadapan.
Secara khusus, kita boleh menggunakan fungsi kehilangan berikut untuk melatih PINN:
L_{pinn}=L_{data}+L_{fizik}
di mana L_{data} ialah kehilangan data, Use untuk mensimulasikan nilai perubahan keadaan yang diketahui. Secara amnya, kita boleh menggunakan ralat min kuasa dua untuk mentakrifkan L_{data} dengan pasti:
L_{data}=frac{1}{N}sum_{i=1}^{N}(u_i-u_{data, i })^2
di mana $N$ ialah bilangan sampel dalam set data, u_i ialah nilai perubahan keadaan yang diramalkan oleh rangkaian saraf dan u_{data,i} ialah nilai perubahan keadaan sebenar yang sepadan dalam set data.
L_{fizik} ialah kehilangan kekangan fizikal, yang digunakan untuk memastikan bahawa rangkaian neural dan perubahan keadaan memenuhi kaedah fizikal. Secara amnya, kita boleh menggunakan bilangan baki untuk mentakrifkan L_{fizik} dengan pasti:
L_{fizik}=frac{1}{N}sum_{i=1}^{N}(F(u_i,frac{ separa u_i}{separa x},x_i,t_i))^2
di mana F ialah kaedah fizikal, frac{separa u_i}{separa x} ialah cerun perubahan keadaan yang diramalkan oleh rangkaian saraf, x_i dan t_i adalah serupa dengan ini Koordinat ruang dan masa i.
Dengan meminimumkan L_{pinn}, kami boleh mensimulasikan data secara serentak dan memenuhi kaedah fizikal, dengan itu mempelajari tingkah laku dinamik sistem.
Sekarang mari kita lihat beberapa demonstrasi PINN yang realistik. Satu contoh biasa ialah mempelajari tingkah laku dinamik kaedah Navier-Stokes. Kaedah Navier-Stokes menerangkan kelakuan gerakan bendalir, yang boleh ditulis dalam bentuk berikut:
rho(frac{partial u}{partial t}+ucdotnabla u)=-nabla p+munabla^2u+ f
Di mana rho ialah ketumpatan bendalir, u ialah halaju bendalir, p ialah tekanan bendalir, mu ialah ketumpatan bendalir, dan f ialah daya luaran. Matlamat kami adalah untuk mempelajari evolusi masa halaju dan tekanan bendalir, serta keadaan sempadan pada sempadan bendalir.
Untuk mencapai matlamat ini, kita boleh mengisi kaedah Navier-Stokes ke dalam rangkaian saraf untuk memudahkan pembelajaran kelajuan dan evolusi masa tekanan. Secara khusus, kita boleh menggunakan kehilangan berikut untuk melatih PINN:
L_{pinn}=L_{data}+L_{fizik}
di mana takrifan L_{data} dan L_{fizik} Sama seperti sebelumnya . Kita boleh menggunakan model dinamik bendalir untuk menjana satu set data pembolehubah keadaan termasuk halaju dan tekanan, dan kemudian menggunakan PINN untuk mensimulasikan perubahan keadaan dan memenuhi kaedah Navier-Stokes. Dengan cara ini, kita boleh mempelajari kelakuan dinamik cecair, termasuk fenomena seperti aliran basah, vorteks dan lapisan sempadan, tanpa terlebih dahulu menentukan model fizikal yang kompleks atau mendapatkan analisis secara manual.
Contoh lain ialah mempelajari tingkah laku kinematik kaedah gerakan gelombang tak linear. Kaedah gerakan gelombang tak linear menerangkan tingkah laku perambatan gerakan gelombang dalam pengenalan, yang boleh ditulis dalam bentuk berikut:
frac{partial^2u}{partial t^2}-c^2nabla^2u+f( u) =0
di mana u ialah amplitud kelajuan gelombang, c ialah kelajuan gelombang, dan f(u) ialah item kualiti tak linear. Matlamat kami adalah untuk mempelajari evolusi masa dinamik gelombang dan keadaan sempadan di sempadan pengenalan.
Untuk mencapai matlamat ini, kami boleh menggabungkan proses gelombang tak linear ke dalam rangkaian saraf untuk memudahkan pembelajaran evolusi epokal pergerakan gelombang. Khususnya, kita boleh menggunakan nombor kerosakan berikut untuk melatih PINN:
L_{pinn}=L_{data}+L_{fizik}
di mana L_{data} dan L_{fizik} ditakrifkan sebagai Sama seperti di atas. Kita boleh menggunakan kaedah berangka untuk menjana satu set data perubahan keadaan yang mengandungi amplitud dan langkah, dan kemudian menggunakan PINN untuk mensimulasikan perubahan keadaan dan memenuhi kaedah gelombang tak linear. Dengan cara ini, kita boleh mempelajari evolusi masa gelombang dalam medium, termasuk fenomena seperti perubahan bentuk, pembiasan dan pantulan paket gelombang, tanpa terlebih dahulu mentakrifkan model fizikal yang kompleks atau mendapatkan analisis secara manual.
Ringkasnya, rangkaian saraf berdasarkan maklumat fizikal ialah kaedah yang menggabungkan model fizikal dan rangkaian saraf, yang boleh menyesuaikan diri dengan pembelajaran bumi sistem dinamik bukan linear yang kompleks sambil mengekalkan kepuasan ketat terhadap undang-undang fizikal. PINN telah digunakan secara meluas dalam mekanik bendalir, akustik, mekanik struktur dan bidang lain, dan telah mencapai beberapa keputusan yang luar biasa. Pada masa hadapan, dengan pembangunan berterusan rangkaian saraf dan teknologi pembezaan automatik, PINN diharapkan akan menjadi alat yang lebih besar, lebih kuat dan lebih serba boleh untuk menyelesaikan pelbagai masalah dinamik tak linear.
Atas ialah kandungan terperinci Pengenalan kepada rangkaian saraf yang didorong oleh maklumat fizikal. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

Video Face Swap
Tukar muka dalam mana-mana video dengan mudah menggunakan alat tukar muka AI percuma kami!

Artikel Panas

Alat panas

Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma

SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan

Hantar Studio 13.0.1
Persekitaran pembangunan bersepadu PHP yang berkuasa

Dreamweaver CS6
Alat pembangunan web visual

SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)

Topik panas
 Kajian kes menggunakan model LSTM dwiarah untuk pengelasan teks
Jan 24, 2024 am 10:36 AM
Kajian kes menggunakan model LSTM dwiarah untuk pengelasan teks
Jan 24, 2024 am 10:36 AM
Model LSTM dwiarah ialah rangkaian saraf yang digunakan untuk pengelasan teks. Berikut ialah contoh mudah yang menunjukkan cara menggunakan LSTM dwiarah untuk tugasan pengelasan teks. Pertama, kita perlu mengimport perpustakaan dan modul yang diperlukan: importosimportnumpyasnpfromkeras.preprocessing.textimportTokenizerfromkeras.preprocessing.sequenceimportpad_sequencesfromkeras.modelsimportSequentialfromkeras.layersimportDense,Em
 Terokai konsep, perbezaan, kebaikan dan keburukan RNN, LSTM dan GRU
Jan 22, 2024 pm 07:51 PM
Terokai konsep, perbezaan, kebaikan dan keburukan RNN, LSTM dan GRU
Jan 22, 2024 pm 07:51 PM
Dalam data siri masa, terdapat kebergantungan antara pemerhatian, jadi ia tidak bebas antara satu sama lain. Walau bagaimanapun, rangkaian saraf tradisional menganggap setiap pemerhatian sebagai bebas, yang mengehadkan keupayaan model untuk memodelkan data siri masa. Untuk menyelesaikan masalah ini, Rangkaian Neural Berulang (RNN) telah diperkenalkan, yang memperkenalkan konsep ingatan untuk menangkap ciri dinamik data siri masa dengan mewujudkan kebergantungan antara titik data dalam rangkaian. Melalui sambungan berulang, RNN boleh menghantar maklumat sebelumnya ke dalam pemerhatian semasa untuk meramalkan nilai masa hadapan dengan lebih baik. Ini menjadikan RNN alat yang berkuasa untuk tugasan yang melibatkan data siri masa. Tetapi bagaimanakah RNN mencapai ingatan seperti ini? RNN merealisasikan ingatan melalui gelung maklum balas dalam rangkaian saraf Ini adalah perbezaan antara RNN dan rangkaian saraf tradisional.
 Mengira operan titik terapung (FLOPS) untuk rangkaian saraf
Jan 22, 2024 pm 07:21 PM
Mengira operan titik terapung (FLOPS) untuk rangkaian saraf
Jan 22, 2024 pm 07:21 PM
FLOPS ialah salah satu piawaian untuk penilaian prestasi komputer, digunakan untuk mengukur bilangan operasi titik terapung sesaat. Dalam rangkaian saraf, FLOPS sering digunakan untuk menilai kerumitan pengiraan model dan penggunaan sumber pengkomputeran. Ia adalah penunjuk penting yang digunakan untuk mengukur kuasa pengkomputeran dan kecekapan komputer. Rangkaian saraf ialah model kompleks yang terdiri daripada berbilang lapisan neuron yang digunakan untuk tugas seperti klasifikasi data, regresi dan pengelompokan. Latihan dan inferens rangkaian saraf memerlukan sejumlah besar pendaraban matriks, konvolusi dan operasi pengiraan lain, jadi kerumitan pengiraan adalah sangat tinggi. FLOPS (FloatingPointOperationsperSecond) boleh digunakan untuk mengukur kerumitan pengiraan rangkaian saraf untuk menilai kecekapan penggunaan sumber pengiraan model. FLOP
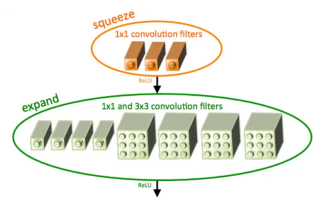 Pengenalan kepada SqueezeNet dan ciri-cirinya
Jan 22, 2024 pm 07:15 PM
Pengenalan kepada SqueezeNet dan ciri-cirinya
Jan 22, 2024 pm 07:15 PM
SqueezeNet ialah algoritma kecil dan tepat yang memberikan keseimbangan yang baik antara ketepatan tinggi dan kerumitan rendah, menjadikannya sesuai untuk sistem mudah alih dan terbenam dengan sumber terhad. Pada 2016, penyelidik dari DeepScale, University of California, Berkeley, dan Stanford University mencadangkan SqueezeNet, rangkaian neural convolutional (CNN) yang padat dan cekap. Dalam beberapa tahun kebelakangan ini, penyelidik telah membuat beberapa penambahbaikan pada SqueezeNet, termasuk SqueezeNetv1.1 dan SqueezeNetv2.0. Penambahbaikan dalam kedua-dua versi bukan sahaja meningkatkan ketepatan tetapi juga mengurangkan kos pengiraan. Ketepatan SqueezeNetv1.1 pada dataset ImageNet
 Penghapusan imej menggunakan rangkaian saraf konvolusi
Jan 23, 2024 pm 11:48 PM
Penghapusan imej menggunakan rangkaian saraf konvolusi
Jan 23, 2024 pm 11:48 PM
Rangkaian neural konvolusi berfungsi dengan baik dalam tugasan menghilangkan imej. Ia menggunakan penapis yang dipelajari untuk menapis bunyi dan dengan itu memulihkan imej asal. Artikel ini memperkenalkan secara terperinci kaedah denoising imej berdasarkan rangkaian neural convolutional. 1. Gambaran Keseluruhan Rangkaian Neural Konvolusi Rangkaian saraf konvolusi ialah algoritma pembelajaran mendalam yang menggunakan gabungan berbilang lapisan konvolusi, lapisan gabungan dan lapisan bersambung sepenuhnya untuk mempelajari dan mengelaskan ciri imej. Dalam lapisan konvolusi, ciri tempatan imej diekstrak melalui operasi konvolusi, dengan itu menangkap korelasi spatial dalam imej. Lapisan pengumpulan mengurangkan jumlah pengiraan dengan mengurangkan dimensi ciri dan mengekalkan ciri utama. Lapisan bersambung sepenuhnya bertanggungjawab untuk memetakan ciri dan label yang dipelajari untuk melaksanakan pengelasan imej atau tugas lain. Reka bentuk struktur rangkaian ini menjadikan rangkaian neural konvolusi berguna dalam pemprosesan dan pengecaman imej.
 Bandingkan persamaan, perbezaan dan hubungan antara lilitan diluaskan dan lilitan atrus
Jan 22, 2024 pm 10:27 PM
Bandingkan persamaan, perbezaan dan hubungan antara lilitan diluaskan dan lilitan atrus
Jan 22, 2024 pm 10:27 PM
Konvolusi diluaskan dan lilitan diluaskan adalah operasi yang biasa digunakan dalam rangkaian neural konvolusi Artikel ini akan memperkenalkan perbezaan dan hubungannya secara terperinci. 1. Konvolusi diluaskan Konvolusi diluaskan, juga dikenali sebagai lilitan diluaskan atau lilitan diluaskan, ialah operasi dalam rangkaian neural konvolusi. Ia adalah lanjutan berdasarkan operasi lilitan tradisional dan meningkatkan medan penerimaan kernel lilitan dengan memasukkan lubang dalam kernel lilitan. Dengan cara ini, rangkaian boleh menangkap lebih banyak ciri yang lebih luas. Konvolusi dilatasi digunakan secara meluas dalam bidang pemprosesan imej dan boleh meningkatkan prestasi rangkaian tanpa menambah bilangan parameter dan jumlah pengiraan. Dengan meluaskan medan penerimaan kernel lilitan, lilitan diluaskan boleh memproses maklumat global dalam imej dengan lebih baik, sekali gus meningkatkan kesan pengekstrakan ciri. Idea utama lilitan diluaskan adalah untuk memperkenalkan beberapa
 Definisi dan analisis struktur rangkaian neural kabur
Jan 22, 2024 pm 09:09 PM
Definisi dan analisis struktur rangkaian neural kabur
Jan 22, 2024 pm 09:09 PM
Rangkaian saraf kabur ialah model hibrid yang menggabungkan logik kabur dan rangkaian saraf untuk menyelesaikan masalah kabur atau tidak pasti yang sukar dikendalikan dengan rangkaian saraf tradisional. Reka bentuknya diilhamkan oleh kekaburan dan ketidakpastian dalam kognisi manusia, jadi ia digunakan secara meluas dalam sistem kawalan, pengecaman corak, perlombongan data dan bidang lain. Seni bina asas rangkaian neural kabur terdiri daripada subsistem kabur dan subsistem saraf. Subsistem kabur menggunakan logik kabur untuk memproses data input dan menukarnya kepada set kabur untuk menyatakan kekaburan dan ketidakpastian data input. Subsistem saraf menggunakan rangkaian saraf untuk memproses set kabur untuk tugasan seperti pengelasan, regresi atau pengelompokan. Interaksi antara subsistem kabur dan subsistem saraf menjadikan rangkaian neural kabur mempunyai keupayaan pemprosesan yang lebih berkuasa dan boleh
 Rangkaian Neural Berkembar: Analisis Prinsip dan Aplikasi
Jan 24, 2024 pm 04:18 PM
Rangkaian Neural Berkembar: Analisis Prinsip dan Aplikasi
Jan 24, 2024 pm 04:18 PM
Rangkaian Neural Siam ialah struktur rangkaian saraf tiruan yang unik. Ia terdiri daripada dua rangkaian neural yang sama yang berkongsi parameter dan berat yang sama. Pada masa yang sama, kedua-dua rangkaian juga berkongsi data input yang sama. Reka bentuk ini diilhamkan oleh kembar, kerana kedua-dua rangkaian saraf adalah sama dari segi struktur. Prinsip rangkaian saraf Siam adalah untuk menyelesaikan tugas tertentu, seperti padanan imej, padanan teks dan pengecaman muka, dengan membandingkan persamaan atau jarak antara dua data input. Semasa latihan, rangkaian cuba untuk memetakan data yang serupa ke wilayah bersebelahan dan data yang tidak serupa ke wilayah yang jauh. Dengan cara ini, rangkaian boleh belajar cara mengklasifikasikan atau memadankan data yang berbeza dan mencapai yang sepadan






