Model medan rawak bersyarat dalam pembelajaran mesin

Medan Rawak Bersyarat (CRF) ialah model grafik kebarangkalian yang digunakan untuk memodelkan taburan kebarangkalian bersama jujukan berlabel. Sebagai model diskriminasi, matlamatnya adalah untuk mempelajari taburan kebarangkalian pembolehubah keluaran Y di bawah keadaan pembolehubah input X. CRF digunakan secara meluas dalam bidang seperti pemprosesan bahasa semula jadi, penglihatan komputer dan bioinformatik. Ia mampu memodelkan data jujukan dan membuat ramalan label dengan mempertimbangkan maklumat kontekstual. Dalam pemprosesan bahasa semula jadi, CRF boleh digunakan untuk tugas seperti pengecaman entiti bernama, penandaan sebahagian daripada pertuturan dan analisis sintaksis. Dalam penglihatan komputer, CRF boleh digunakan untuk tugasan seperti pembahagian imej dan pengecaman objek. Dalam bioinformatik, CRF boleh digunakan untuk tugas seperti pengecaman gen dan ramalan struktur protein. Dengan mengambil kira ciri global dan maklumat kontekstual jujukan, CRF boleh meningkatkan prestasi dan keteguhan model Andaian asas CRF ialah, memandangkan urutan input X, pelbagai kedudukan jujukan keluaran Y adalah bebas bersyarat. Maksudnya, setiap pembolehubah keluaran Yi hanya bergantung pada pembolehubah input Xi yang sepadan dan pembolehubah output Yi-1 dan Yi+1 pada kedudukan sebelumnya dan seterusnya, dan tidak ada kena mengena dengan pembolehubah keluaran pada kedudukan lain. Andaian ini membolehkan CRF menangani masalah penandaan jujukan dengan cekap, seperti pengecaman entiti bernama, penandaan sebahagian daripada pertuturan dan analisis ketulan. Andaian kebebasan CRF membolehkan model menangkap kebergantungan tempatan dalam jujukan input, dengan itu meningkatkan ketepatan dan prestasi anotasi.
Model CRF boleh dinyatakan sebagai graf tidak berarah, di mana setiap nod mewakili pembolehubah keluaran Yi, dan tepi antara nod mewakili hubungan pergantungan antara dua pembolehubah keluaran. Khususnya, jika terdapat pergantungan antara dua pembolehubah keluaran Yi dan Yj, maka terdapat kelebihan yang menghubungkannya. Berat tepi mewakili kebarangkalian bersyarat yang sepadan, yang boleh dianggarkan dengan mempelajari data latihan.
Proses latihan CRF melibatkan memaksimumkan fungsi log-kemungkinan data latihan, termasuk hasil darab kebarangkalian bersyarat pada pembolehubah yang diperhatikan (pembolehubah input X) dan kebarangkalian bersyarat pada pembolehubah output (jujukan berlabel Y) . Dengan menggunakan algoritma pengoptimuman seperti keturunan kecerunan stokastik, fungsi ini boleh dimaksimumkan untuk mendapatkan parameter model.
Proses ramalan CRF termasuk mengira taburan kebarangkalian bersyarat bagi urutan output Y di bawah urutan input X, dan memilih urutan output dengan kebarangkalian tertinggi sebagai hasil ramalan. Untuk pengiraan yang cekap, algoritma ke hadapan-belakang boleh digunakan.
Selain CRF Rantaian Linear asas, terdapat juga model medan rawak bersyarat yang lebih kompleks, seperti CRF Rantaian Bukan Linear dan Rangkaian Neural Medan Rawak Bersyarat (CRF) -NN). Model ini boleh mengendalikan masalah pelabelan jujukan yang lebih kompleks, tetapi juga memerlukan lebih banyak sumber pengkomputeran dan lebih banyak data latihan.
CRF, sebagai algoritma pembelajaran tanpa pengawasan, telah digunakan secara meluas dalam bidang seperti pemprosesan bahasa semula jadi, penglihatan komputer dan bioinformatik. Dalam bidang pemprosesan bahasa semula jadi, CRF sering digunakan untuk tugas seperti pengecaman entiti bernama, penandaan sebahagian daripada pertuturan, analisis sintaksis dan klasifikasi teks. Dalam bidang penglihatan komputer, CRF sering digunakan untuk tugasan seperti pembahagian imej, penjejakan sasaran, dan anggaran pose. Dalam bidang bioinformatik, CRF sering digunakan untuk tugas seperti pengenalan gen dan ramalan struktur protein.
Atas ialah kandungan terperinci Model medan rawak bersyarat dalam pembelajaran mesin. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

Video Face Swap
Tukar muka dalam mana-mana video dengan mudah menggunakan alat tukar muka AI percuma kami!

Artikel Panas

Alat panas

Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma

SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan

Hantar Studio 13.0.1
Persekitaran pembangunan bersepadu PHP yang berkuasa

Dreamweaver CS6
Alat pembangunan web visual

SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)

Topik panas
 1677
1677
 14
14
 1430
1430
 52
52
 1333
1333
 25
25
 1278
1278
 29
29
 1257
1257
 24
24
 Bytedance Cutting melancarkan keahlian super SVIP: 499 yuan untuk langganan tahunan berterusan, menyediakan pelbagai fungsi AI
Jun 28, 2024 am 03:51 AM
Bytedance Cutting melancarkan keahlian super SVIP: 499 yuan untuk langganan tahunan berterusan, menyediakan pelbagai fungsi AI
Jun 28, 2024 am 03:51 AM
Laman web ini melaporkan pada 27 Jun bahawa Jianying ialah perisian penyuntingan video yang dibangunkan oleh FaceMeng Technology, anak syarikat ByteDance Ia bergantung pada platform Douyin dan pada asasnya menghasilkan kandungan video pendek untuk pengguna platform tersebut Windows , MacOS dan sistem pengendalian lain. Jianying secara rasmi mengumumkan peningkatan sistem keahliannya dan melancarkan SVIP baharu, yang merangkumi pelbagai teknologi hitam AI, seperti terjemahan pintar, penonjolan pintar, pembungkusan pintar, sintesis manusia digital, dsb. Dari segi harga, yuran bulanan untuk keratan SVIP ialah 79 yuan, yuran tahunan ialah 599 yuan (nota di laman web ini: bersamaan dengan 49.9 yuan sebulan), langganan bulanan berterusan ialah 59 yuan sebulan, dan langganan tahunan berterusan ialah 499 yuan setahun (bersamaan dengan 41.6 yuan sebulan) . Di samping itu, pegawai yang dipotong juga menyatakan bahawa untuk meningkatkan pengalaman pengguna, mereka yang telah melanggan VIP asal
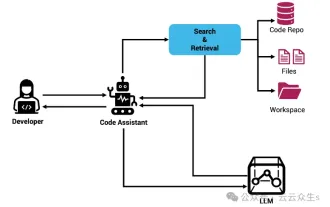 Pembantu pengekodan AI yang ditambah konteks menggunakan Rag dan Sem-Rag
Jun 10, 2024 am 11:08 AM
Pembantu pengekodan AI yang ditambah konteks menggunakan Rag dan Sem-Rag
Jun 10, 2024 am 11:08 AM
Tingkatkan produktiviti, kecekapan dan ketepatan pembangun dengan menggabungkan penjanaan dipertingkatkan semula dan memori semantik ke dalam pembantu pengekodan AI. Diterjemah daripada EnhancingAICodingAssistantswithContextUsingRAGandSEM-RAG, pengarang JanakiramMSV. Walaupun pembantu pengaturcaraan AI asas secara semulajadi membantu, mereka sering gagal memberikan cadangan kod yang paling relevan dan betul kerana mereka bergantung pada pemahaman umum bahasa perisian dan corak penulisan perisian yang paling biasa. Kod yang dijana oleh pembantu pengekodan ini sesuai untuk menyelesaikan masalah yang mereka bertanggungjawab untuk menyelesaikannya, tetapi selalunya tidak mematuhi piawaian pengekodan, konvensyen dan gaya pasukan individu. Ini selalunya menghasilkan cadangan yang perlu diubah suai atau diperhalusi agar kod itu diterima ke dalam aplikasi
 Bolehkah penalaan halus benar-benar membolehkan LLM mempelajari perkara baharu: memperkenalkan pengetahuan baharu boleh menjadikan model menghasilkan lebih banyak halusinasi
Jun 11, 2024 pm 03:57 PM
Bolehkah penalaan halus benar-benar membolehkan LLM mempelajari perkara baharu: memperkenalkan pengetahuan baharu boleh menjadikan model menghasilkan lebih banyak halusinasi
Jun 11, 2024 pm 03:57 PM
Model Bahasa Besar (LLM) dilatih pada pangkalan data teks yang besar, di mana mereka memperoleh sejumlah besar pengetahuan dunia sebenar. Pengetahuan ini dibenamkan ke dalam parameter mereka dan kemudiannya boleh digunakan apabila diperlukan. Pengetahuan tentang model ini "diperbaharui" pada akhir latihan. Pada akhir pra-latihan, model sebenarnya berhenti belajar. Selaraskan atau perhalusi model untuk mempelajari cara memanfaatkan pengetahuan ini dan bertindak balas dengan lebih semula jadi kepada soalan pengguna. Tetapi kadangkala pengetahuan model tidak mencukupi, dan walaupun model boleh mengakses kandungan luaran melalui RAG, ia dianggap berfaedah untuk menyesuaikan model kepada domain baharu melalui penalaan halus. Penalaan halus ini dilakukan menggunakan input daripada anotasi manusia atau ciptaan LLM lain, di mana model menemui pengetahuan dunia sebenar tambahan dan menyepadukannya
 Tujuh Soalan Temuduga Teknikal GenAI & LLM yang Cool
Jun 07, 2024 am 10:06 AM
Tujuh Soalan Temuduga Teknikal GenAI & LLM yang Cool
Jun 07, 2024 am 10:06 AM
Untuk mengetahui lebih lanjut tentang AIGC, sila layari: 51CTOAI.x Komuniti https://www.51cto.com/aigc/Translator|Jingyan Reviewer|Chonglou berbeza daripada bank soalan tradisional yang boleh dilihat di mana-mana sahaja di Internet memerlukan pemikiran di luar kotak. Model Bahasa Besar (LLM) semakin penting dalam bidang sains data, kecerdasan buatan generatif (GenAI) dan kecerdasan buatan. Algoritma kompleks ini meningkatkan kemahiran manusia dan memacu kecekapan dan inovasi dalam banyak industri, menjadi kunci kepada syarikat untuk kekal berdaya saing. LLM mempunyai pelbagai aplikasi Ia boleh digunakan dalam bidang seperti pemprosesan bahasa semula jadi, penjanaan teks, pengecaman pertuturan dan sistem pengesyoran. Dengan belajar daripada sejumlah besar data, LLM dapat menjana teks
 Lima sekolah pembelajaran mesin yang anda tidak tahu
Jun 05, 2024 pm 08:51 PM
Lima sekolah pembelajaran mesin yang anda tidak tahu
Jun 05, 2024 pm 08:51 PM
Pembelajaran mesin ialah cabang penting kecerdasan buatan yang memberikan komputer keupayaan untuk belajar daripada data dan meningkatkan keupayaan mereka tanpa diprogramkan secara eksplisit. Pembelajaran mesin mempunyai pelbagai aplikasi dalam pelbagai bidang, daripada pengecaman imej dan pemprosesan bahasa semula jadi kepada sistem pengesyoran dan pengesanan penipuan, dan ia mengubah cara hidup kita. Terdapat banyak kaedah dan teori yang berbeza dalam bidang pembelajaran mesin, antaranya lima kaedah yang paling berpengaruh dipanggil "Lima Sekolah Pembelajaran Mesin". Lima sekolah utama ialah sekolah simbolik, sekolah sambungan, sekolah evolusi, sekolah Bayesian dan sekolah analogi. 1. Simbolisme, juga dikenali sebagai simbolisme, menekankan penggunaan simbol untuk penaakulan logik dan ekspresi pengetahuan. Aliran pemikiran ini percaya bahawa pembelajaran adalah proses penolakan terbalik, melalui sedia ada
 Untuk menyediakan tanda aras dan sistem penilaian menjawab soalan saintifik dan kompleks baharu untuk model besar, UNSW, Argonne, University of Chicago dan institusi lain bersama-sama melancarkan rangka kerja SciQAG
Jul 25, 2024 am 06:42 AM
Untuk menyediakan tanda aras dan sistem penilaian menjawab soalan saintifik dan kompleks baharu untuk model besar, UNSW, Argonne, University of Chicago dan institusi lain bersama-sama melancarkan rangka kerja SciQAG
Jul 25, 2024 am 06:42 AM
Editor |ScienceAI Question Answering (QA) set data memainkan peranan penting dalam mempromosikan penyelidikan pemprosesan bahasa semula jadi (NLP). Set data QA berkualiti tinggi bukan sahaja boleh digunakan untuk memperhalusi model, tetapi juga menilai dengan berkesan keupayaan model bahasa besar (LLM), terutamanya keupayaan untuk memahami dan menaakul tentang pengetahuan saintifik. Walaupun pada masa ini terdapat banyak set data QA saintifik yang meliputi bidang perubatan, kimia, biologi dan bidang lain, set data ini masih mempunyai beberapa kekurangan. Pertama, borang data adalah agak mudah, kebanyakannya adalah soalan aneka pilihan. Ia mudah dinilai, tetapi mengehadkan julat pemilihan jawapan model dan tidak dapat menguji sepenuhnya keupayaan model untuk menjawab soalan saintifik. Sebaliknya, Soal Jawab terbuka
 SK Hynix akan memaparkan produk berkaitan AI baharu pada 6 Ogos: HBM3E 12 lapisan, NAND 321 tinggi, dsb.
Aug 01, 2024 pm 09:40 PM
SK Hynix akan memaparkan produk berkaitan AI baharu pada 6 Ogos: HBM3E 12 lapisan, NAND 321 tinggi, dsb.
Aug 01, 2024 pm 09:40 PM
Menurut berita dari laman web ini pada 1 Ogos, SK Hynix mengeluarkan catatan blog hari ini (1 Ogos), mengumumkan bahawa ia akan menghadiri Global Semiconductor Memory Summit FMS2024 yang akan diadakan di Santa Clara, California, Amerika Syarikat dari 6 hingga 8 Ogos, mempamerkan banyak produk penjanaan teknologi baru. Pengenalan kepada Sidang Kemuncak Memori dan Penyimpanan Masa Depan (FutureMemoryandStorage), dahulunya Sidang Kemuncak Memori Flash (FlashMemorySummit) terutamanya untuk pembekal NAND, dalam konteks peningkatan perhatian kepada teknologi kecerdasan buatan, tahun ini dinamakan semula sebagai Sidang Kemuncak Memori dan Penyimpanan Masa Depan (FutureMemoryandStorage) kepada jemput vendor DRAM dan storan serta ramai lagi pemain. Produk baharu SK hynix dilancarkan tahun lepas
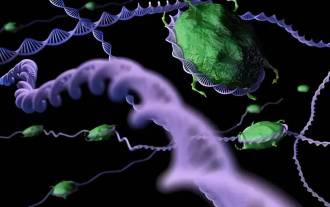 Prestasi SOTA, kaedah AI ramalan pertalian protein-ligan pelbagai mod Xiamen, menggabungkan maklumat permukaan molekul buat kali pertama
Jul 17, 2024 pm 06:37 PM
Prestasi SOTA, kaedah AI ramalan pertalian protein-ligan pelbagai mod Xiamen, menggabungkan maklumat permukaan molekul buat kali pertama
Jul 17, 2024 pm 06:37 PM
Editor |. KX Dalam bidang penyelidikan dan pembangunan ubat, meramalkan pertalian pengikatan protein dan ligan dengan tepat dan berkesan adalah penting untuk pemeriksaan dan pengoptimuman ubat. Walau bagaimanapun, kajian semasa tidak mengambil kira peranan penting maklumat permukaan molekul dalam interaksi protein-ligan. Berdasarkan ini, penyelidik dari Universiti Xiamen mencadangkan rangka kerja pengekstrakan ciri berbilang mod (MFE) novel, yang buat pertama kalinya menggabungkan maklumat mengenai permukaan protein, struktur dan jujukan 3D, dan menggunakan mekanisme perhatian silang untuk membandingkan ciri modaliti yang berbeza penjajaran. Keputusan eksperimen menunjukkan bahawa kaedah ini mencapai prestasi terkini dalam meramalkan pertalian mengikat protein-ligan. Tambahan pula, kajian ablasi menunjukkan keberkesanan dan keperluan maklumat permukaan protein dan penjajaran ciri multimodal dalam rangka kerja ini. Penyelidikan berkaitan bermula dengan "S




