
Kernel Model Gaussian Processes (KMGPs) ialah alat yang canggih untuk mengendalikan kerumitan pelbagai set data. Ia memanjangkan konsep proses Gaussian tradisional melalui fungsi kernel. Artikel ini akan membincangkan secara terperinci asas teori, aplikasi praktikal dan cabaran KMGP.
Proses Gaussian model kernel ialah lanjutan daripada proses Gaussian tradisional dan digunakan dalam pembelajaran mesin dan statistik. Sebelum memahami kmgp, anda perlu menguasai pengetahuan asas proses Gaussian, dan kemudian memahami peranan model kernel.
Proses Gaussian ialah set pembolehubah rawak, dengan bilangan pembolehubah terhad yang diedarkan bersama oleh Gaussian, digunakan untuk menentukan taburan kebarangkalian fungsi.
Proses Gaussian biasanya digunakan dalam regresi dan tugas klasifikasi dalam pembelajaran mesin dan boleh digunakan untuk menyesuaikan taburan kebarangkalian data.
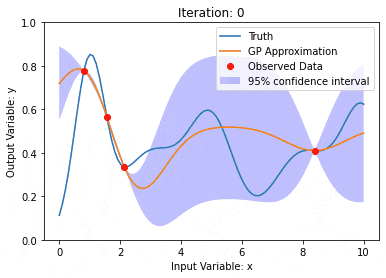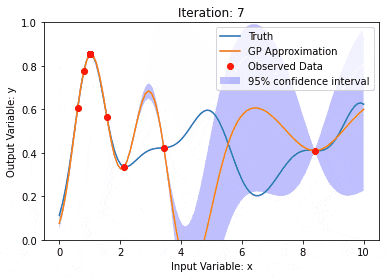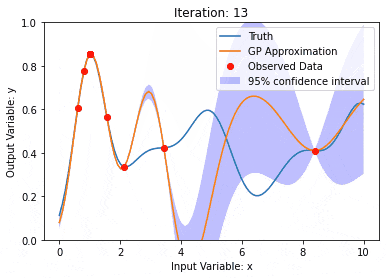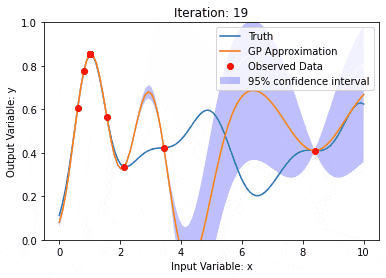
Ciri penting proses Gaussian ialah keupayaan untuk memberikan anggaran ketidakpastian dan ramalan, yang sangat berguna dalam tugas memahami keyakinan ramalan adalah sama pentingnya dengan ramalan itu sendiri.
Dalam proses Gaussian, fungsi kernel (atau fungsi kovarians) digunakan untuk mengukur persamaan antara titik data yang berbeza. Fungsi kernel mengambil dua input dan mengira skor persamaan antara mereka.
Terdapat pelbagai jenis isirong seperti fungsi asas linear, polinomial dan jejari (RBF). Setiap teras mempunyai ciri yang berbeza, dan teras yang sesuai boleh dipilih mengikut masalah.
Dalam proses Gaussian, pemodelan kernel ialah proses memilih dan mengoptimumkan fungsi kernel untuk menangkap corak asas dalam data dengan terbaik. Langkah ini sangat penting kerana pemilihan dan konfigurasi kernel boleh menjejaskan prestasi proses Gaussian dengan ketara.
KMGPs ialah lanjutan daripada GP standard (Gaussian Process), memfokuskan pada aplikasi fungsi kernel. Berbanding dengan GP standard, KMGP memberi lebih perhatian kepada menyesuaikan fungsi kernel yang kompleks atau direka khas mengikut jenis data atau masalah tertentu. Pendekatan ini amat berguna apabila data adalah kompleks dan fungsi kernel standard gagal menangkap perhubungan asas. Walau bagaimanapun, mereka bentuk dan menala fungsi kernel dalam KMGP adalah mencabar dan selalunya memerlukan pengetahuan domain yang mendalam dan pengalaman profesional dalam domain masalah dan pemodelan statistik.
Proses Gaussian Model Kernel ialah alat yang canggih dalam pembelajaran statistik, menyediakan cara yang fleksibel dan berkuasa untuk memodelkan set data yang kompleks. Mereka amat dihargai kerana keupayaan mereka untuk memberikan anggaran ketidakpastian dan kebolehsuaian mereka untuk mendamaikan jenis data yang berbeza melalui penyesuaian tersuai.
Inti yang direka dengan baik dalam KMGP boleh memodelkan fenomena kompleks seperti aliran tak linear, periodicity dan heteroskedasticity (paras hingar yang berbeza-beza) dalam data. Jadi ia memerlukan pengetahuan domain yang mendalam dan pemahaman yang menyeluruh tentang pemodelan statistik.
KMGP mempunyai aplikasi dalam banyak bidang. Dalam geostatistik, mereka memodelkan data spatial untuk menangkap variasi geografi yang mendasari. Dalam kewangan, ia digunakan untuk meramalkan harga saham, menjelaskan sifat pasaran kewangan yang tidak stabil dan kompleks. Dalam sistem robotik dan kawalan, KMGP memodelkan dan meramalkan kelakuan sistem dinamik di bawah ketidakpastian.
Kami menggunakan set data sintetik untuk mencipta contoh kod Python yang lengkap Di sini kami menggunakan perpustakaan GPy, iaitu perpustakaan dalam python yang pakar dalam mengendalikan proses Gaussian.
pip install numpy matplotlib GPy
Import library
import numpy as np import matplotlib.pyplot as plt import GPy
Kemudian kami akan mencipta set data sintetik menggunakan numpy.
X = np.linspace(0, 10, 100)[:, None] Y = np.sin(X) + np.random.normal(0, 0.1, X.shape)
Takrif dan latih model proses Gaussian menggunakan GPy
kernel = GPy.kern.RBF(input_dim=1, variance=1., lengthscale=1.) model = GPy.models.GPRegression(X, Y, kernel) model.optimize(messages=True)
Selepas melatih model, kami akan menggunakannya untuk membuat ramalan pada set data ujian. Kemudian plot graf untuk menggambarkan prestasi model.
X_test = np.linspace(-2, 12, 200)[:, None] Y_pred, Y_var = model.predict(X_test) plt.figure(figsize=(10, 5)) plt.plot(X_test, Y_pred, 'r-', lw=2, label='Prediction') plt.fill_between(X_test.flatten(), (Y_pred - 2*np.sqrt(Y_var)).flatten(), (Y_pred + 2*np.sqrt(Y_var)).flatten(), alpha=0.5, color='pink', label='Confidence Interval') plt.scatter(X, Y, c='b', label='Training Data') plt.xlabel('X') plt.ylabel('Y') plt.title('Kernel Modeled Gaussian Process Regression') plt.legend() plt.show()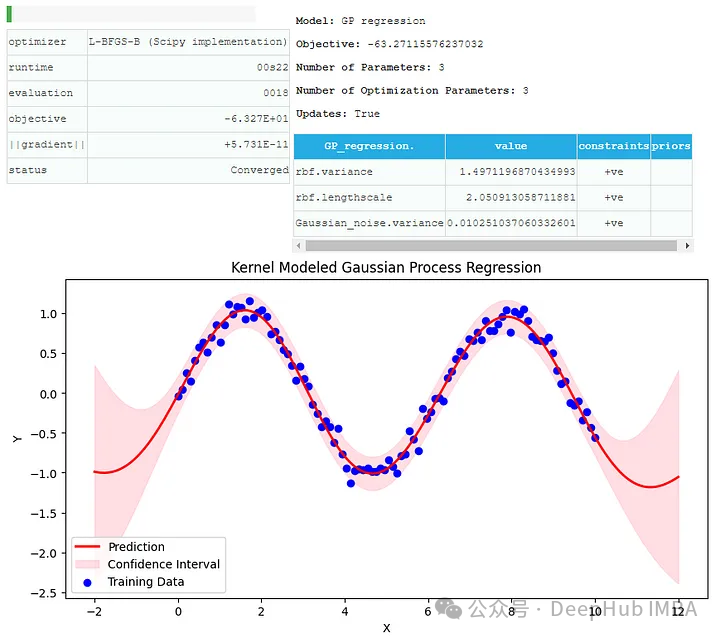
Di sini kita menggunakan model regresi proses Gaussian dengan kernel RBF, dan kita boleh melihat ramalan dan data latihan serta selang keyakinan.
Model kernel Proses Gaussian mewakili kemajuan besar dalam bidang pembelajaran statistik, menyediakan rangka kerja yang fleksibel dan berkuasa untuk memahami set data yang kompleks. GPy juga mengandungi pada asasnya semua fungsi kernel yang boleh kita lihat Berikut ialah tangkapan skrin dokumen rasmi:
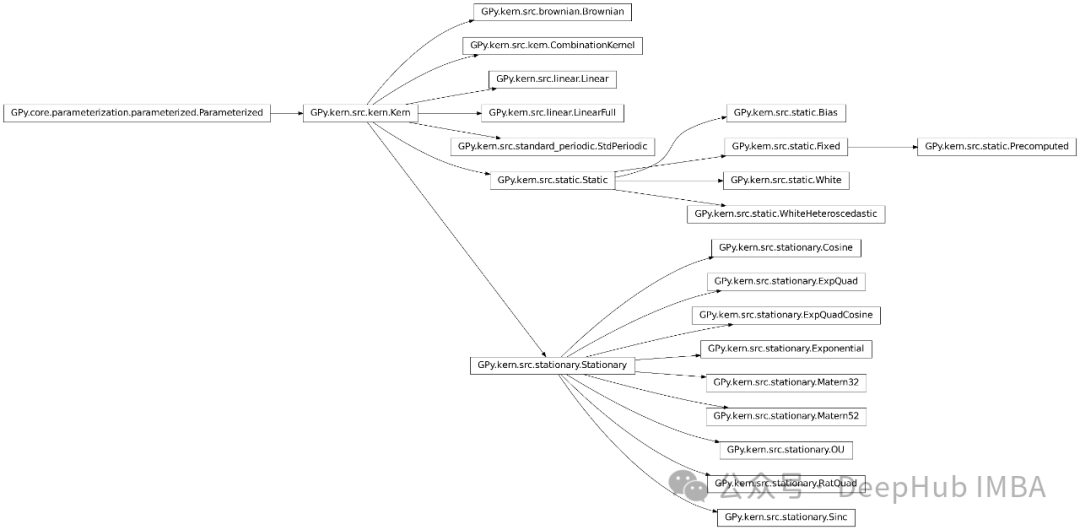
Untuk data yang berbeza, anda perlu memilih hiperparameter kernel fungsi kernel yang berbeza. Berikut ialah aliran GPy A rasmi carta diberi
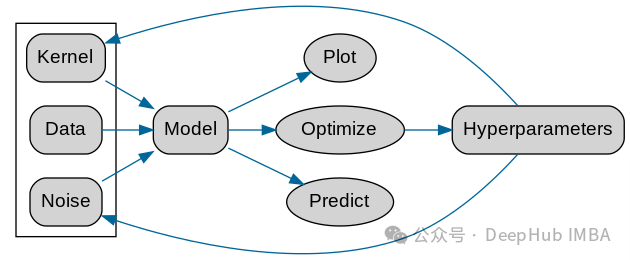
Atas ialah kandungan terperinci Pemodelan data menggunakan Kernel Model Gaussian Processes (KMGPs). Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
 Penggunaan arahan sumber dalam linux
Penggunaan arahan sumber dalam linux
 Penyemak keserasian
Penyemak keserasian
 Bagaimana untuk menukar devc++ kepada bahasa Cina
Bagaimana untuk menukar devc++ kepada bahasa Cina
 proses paparan linux
proses paparan linux
 Bagaimana untuk menyelesaikan masalah bahawa pintasan IE tidak boleh dipadamkan
Bagaimana untuk menyelesaikan masalah bahawa pintasan IE tidak boleh dipadamkan
 Perkara yang perlu dilakukan jika chrome tidak dapat memuatkan pemalam
Perkara yang perlu dilakukan jika chrome tidak dapat memuatkan pemalam
 seni bina c/s dan seni bina b/s
seni bina c/s dan seni bina b/s
 Apakah pelayan yang terdapat di web?
Apakah pelayan yang terdapat di web?




