Asas AI4Science: rangkaian neural graf geometri, semakan paling komprehensif ada di sini! Renmin University of China Hillhouse mengeluarkan bersama makmal AI Tencent, Universiti Tsinghua, Stanford, dsb.

Editor |. XS

Nature menerbitkan dua hasil penyelidikan penting pada November 2023: teknologi sintesis protein Chroma dan kaedah reka bentuk bahan kristal GNoME. Kedua-dua kajian menggunakan rangkaian saraf graf sebagai alat untuk memproses data saintifik.

Malah, rangkaian saraf graf, terutamanya rangkaian saraf graf geometri, sentiasa menjadi alat penting untuk penyelidikan kecerdasan saintifik (AI untuk Sains). Ini kerana sistem fizikal seperti zarah, molekul, protein dan kristal dalam bidang saintifik boleh dimodelkan kepada struktur data khas—graf geometri.

Berbeza daripada rajah topologi umum, untuk menerangkan sistem fizikal dengan lebih baik, rajah geometri menambah maklumat spatial yang sangat diperlukan dan perlu memenuhi simetri fizikal terjemahan, putaran dan lilitan. Memandangkan keunggulan rangkaian saraf graf geometri untuk memodelkan sistem fizikal, pelbagai kaedah telah muncul dalam beberapa tahun kebelakangan ini, dan bilangan kertas kerja terus berkembang.

Baru-baru ini, Renmin University of China Hillhouse, bersama dengan Tencent AI Lab, Tsinghua University, Stanford dan institusi lain, mengeluarkan kertas ulasan: "A Survey of Geometric Graph Neural Networks: Data Structures, Models and Applications". Berdasarkan pengenalan ringkas kepada pengetahuan teori seperti teori kumpulan dan simetri, kajian ini mengkaji secara sistematik literatur rangkaian saraf graf geometri yang berkaitan daripada struktur dan model data kepada pelbagai aplikasi saintifik.

Pautan kertas:https://arxiv.org/abs/2403.00485

Pautan GitHub:https://github.com/RUC-GLAD/GGNN4ScienceDalam ulasan ini

meneliti lebih daripada 300 rujukan, kami meringkaskan 3 model rangkaian saraf graf geometri yang berbeza, memperkenalkan kaedah berkaitan untuk sejumlah 23 tugasan berbeza pada pelbagai data saintifik seperti zarah, molekul dan protein, dan mengumpul lebih daripada 50 set data yang berkaitan. Akhir sekali, semakan menantikan arah penyelidikan masa hadapan, termasuk model asas graf geometri, gabungan dengan model bahasa besar, dsb.

Berikut adalah pengenalan ringkas untuk setiap bab.

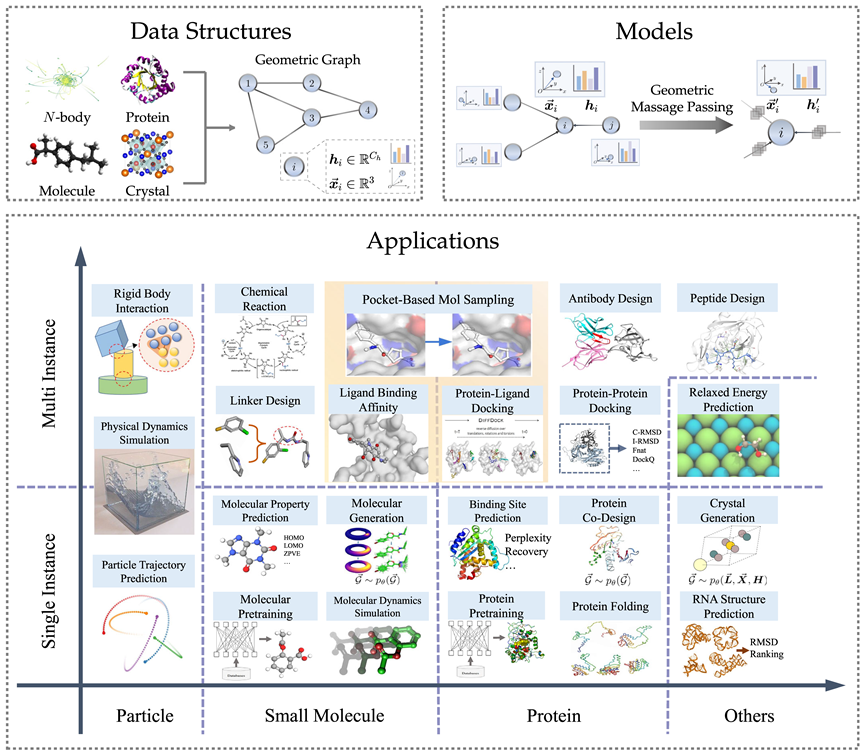
Struktur data graf geometri

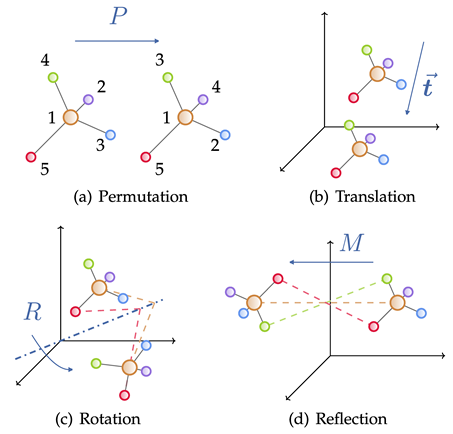
Graf geometri terdiri daripada matriks bersebelahan, ciri nod, maklumat geometri nod (seperti koordinat). Dalam ruang Euclidean, angka geometri biasanya menunjukkan simetri fizikal terjemahan, putaran dan pantulan Kumpulan biasanya digunakan untuk menggambarkan transformasi ini, termasuk kumpulan Euclidean, kumpulan terjemahan, kumpulan ortogon, kumpulan pilih atur, dll. Secara intuitif, ia boleh difahami sebagai gabungan empat operasi: anjakan, terjemahan, putaran dan membalikkan dalam susunan tertentu.

Bagi kebanyakan bidang AI untuk Sains, graf geometri ialah kaedah perwakilan yang berkuasa dan serba boleh, yang boleh digunakan untuk mewakili banyak sistem fizikal, termasuk molekul kecil, protein, kristal, awan titik fizikal, dsb.

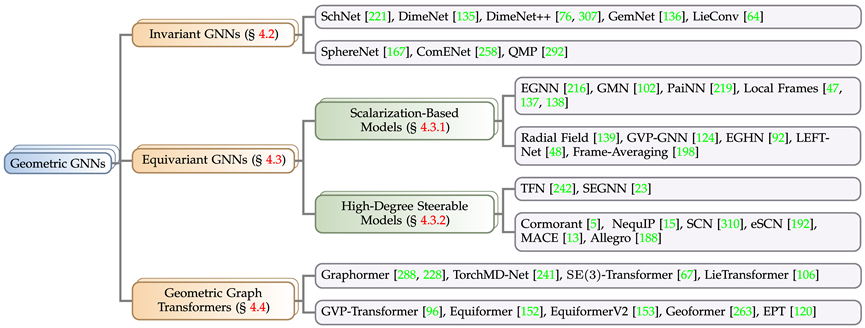
Model rangkaian saraf graf geometri

Mengikut keperluan simetri matlamat penyelesaian dalam masalah sebenar, artikel ini membahagikan rangkaian saraf graf geometri kepada tiga kategori: model invarian dan model Geometri Setara, dan model Graph Transformer diilhamkan oleh seni bina Transformer, di mana model setara dibahagikan kepada model berasaskan skalarisasi dan model boleh dikendalikan darjah tinggi berdasarkan pengharmonian sfera (Model Boleh Dikendali Darjah Tinggi). Mengikut peraturan di atas, artikel itu mengumpul dan mengkategorikan model rangkaian saraf graf geometri yang terkenal dalam beberapa tahun kebelakangan ini.

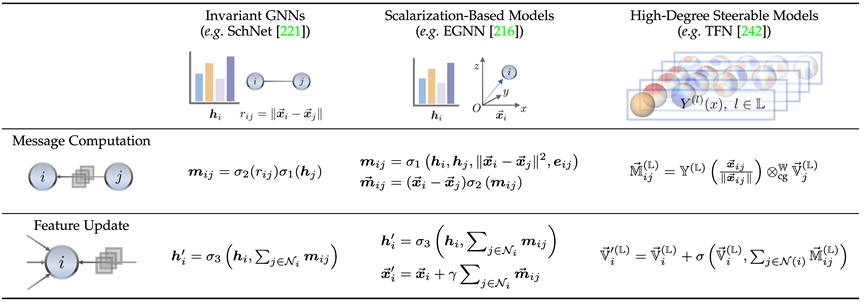
Di sini kami memperkenalkan secara ringkas hubungan antara model invarian (SchNet[1]), model kaedah skalar (EGNN[2]), dan model terkawal peringkat tinggi (TFN[3]) melalui kerja perwakilan setiap cabang dan perbezaan. Boleh didapati bahawa ketiga-tiganya menggunakan mekanisme hantaran mesej, tetapi dua yang terakhir, yang merupakan model setara, memperkenalkan hantaran mesej geometri tambahan.

Model invarian terutamanya menggunakan ciri nod itu sendiri (seperti jenis atom, jisim, cas, dsb.) dan ciri invarian antara atom (seperti jarak, sudut [4], sudut dihedral [5]), dsb. . untuk mengira mesej Kemudian disebarkan.

Selain itu, kaedah penskalaan tambahan memperkenalkan maklumat geometri melalui perbezaan koordinat antara nod, dan secara linear menggabungkan maklumat invarian sebagai berat maklumat geometri untuk mencapai pengenalan kesetaraan.

Model terkawal tertib tinggi menggunakan matriks Spherical Harmonik dan Wigner-D tertib tinggi untuk mewakili maklumat geometri sistem ini mengawal susunan perwakilan tidak boleh dikurangkan melalui pekali Clebsch–Gordan dalam mekanik kuantum proses.

Ketepatan rangkaian saraf graf geometri dipertingkatkan dengan banyak melalui simetri yang dijamin oleh reka bentuk jenis ini, dan ia juga bersinar dalam tugas penjanaan.

Rajah di bawah menunjukkan keputusan tiga tugas ramalan sifat molekul, dok protein-ligan dan reka bentuk antibodi (penjanaan) menggunakan rangkaian saraf graf geometri dan model tradisional pada tiga set data QM9, PDBBind dan SabDab It dapat dilihat dengan jelas bahawa Kelebihan rangkaian saraf graf geometri.

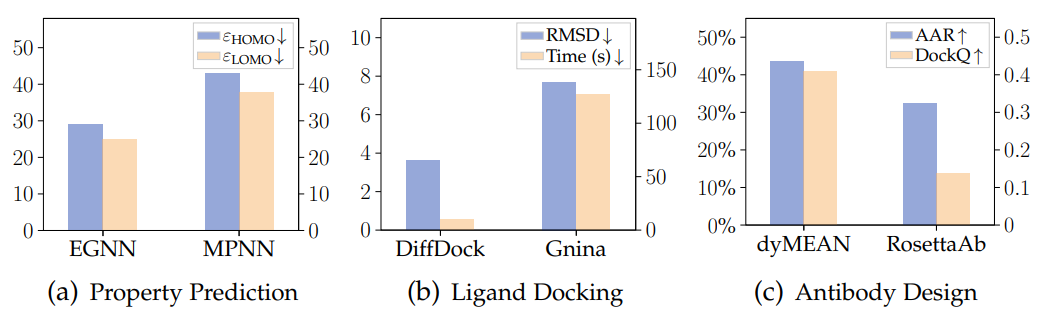
Aplikasi Saintifik

Dari segi aplikasi saintifik, semakan meliputi fizik (zarah), biokimia (molekul kecil, protein) dan senario aplikasi lain seperti kristal, definisi tugas dan mulakan jaminan simetri yang diperlukan , set data yang biasa digunakan dalam setiap tugasan dan idea reka bentuk model klasik dalam jenis tugasan ini diperkenalkan.

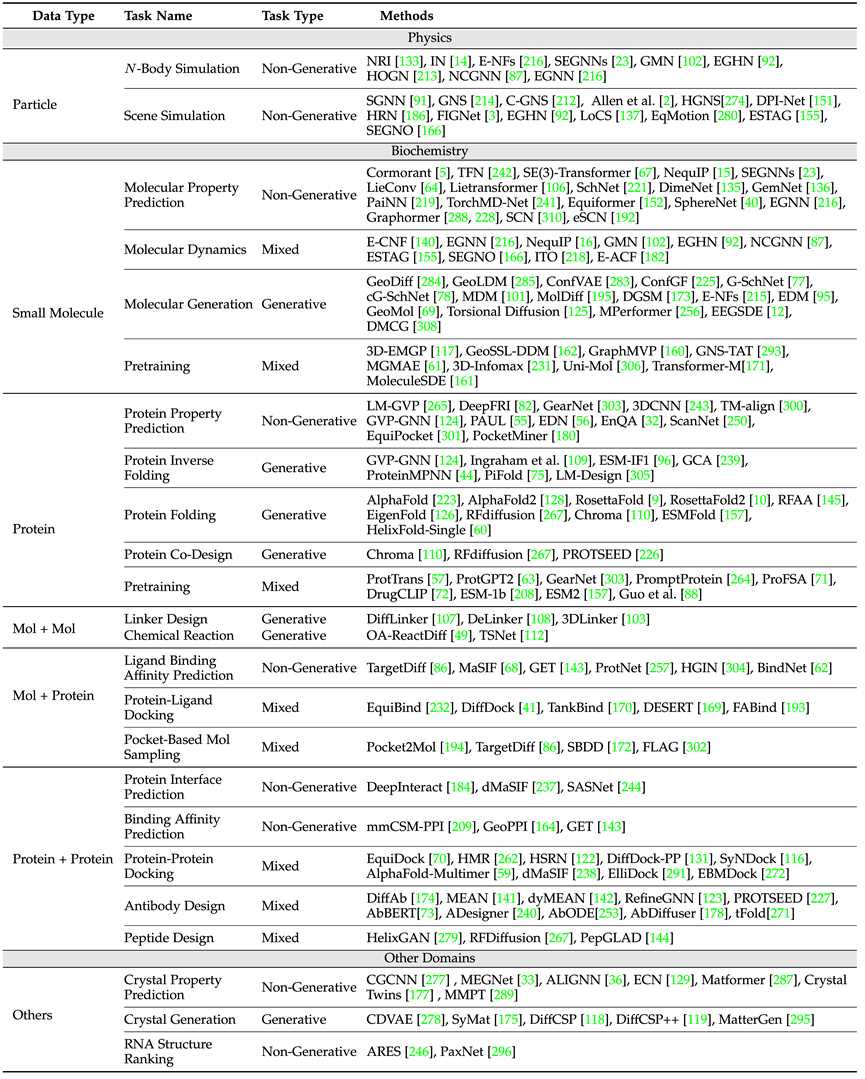
Jadual di atas menunjukkan tugas biasa dan model klasik dalam pelbagai bidang Antaranya, mengikut contoh tunggal dan berbilang kejadian (seperti tindak balas kimia, yang memerlukan penyertaan berbilang molekul), artikel itu membezakan molekul kecil secara berasingan. molekul kecil, molekul kecil -Protein, protein - tiga bidang protein.

Untuk memudahkan reka bentuk model dan pembangunan percubaan dalam lapangan dengan lebih baik, artikel itu mengira set data biasa dan penanda aras untuk dua jenis tugasan berdasarkan satu tika dan berbilang kejadian, serta merekodkan saiz sampel dan jenis tugasan set data yang berbeza. .

Jadual berikut meringkaskan set data tugasan satu contoh biasa.

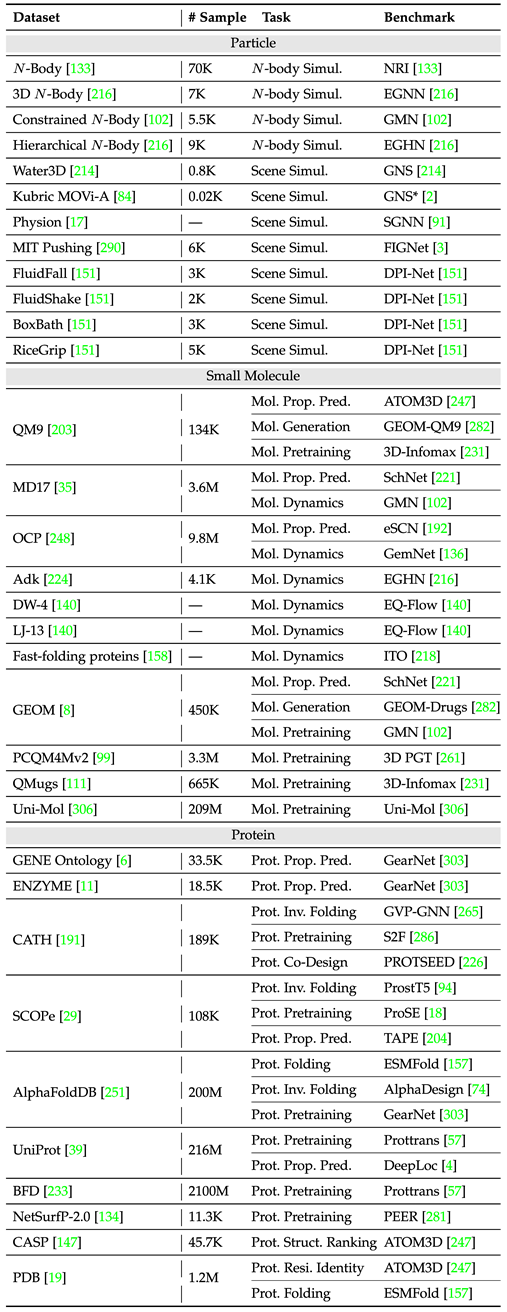
Jadual berikut menyusun set data tugasan berbilang contoh biasa. . keunggulan model asas telah dicerminkan sepenuhnya dalam kemajuan ketara model siri GPT. Bagaimana untuk menjalankan reka bentuk yang munasabah dalam ruang tugas, ruang data dan ruang model, untuk memperkenalkan idea ini ke dalam reka bentuk rangkaian neural graf geometri, masih menjadi masalah terbuka yang menarik.

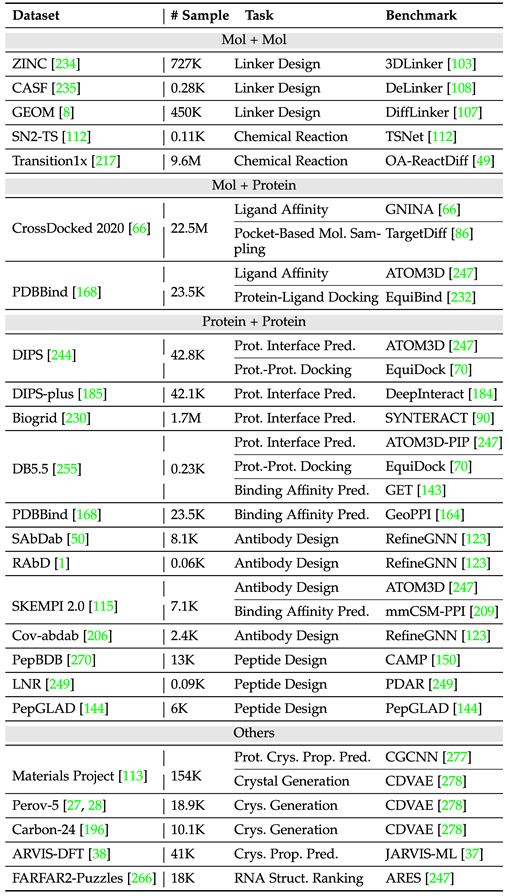2. Kitaran latihan model yang cekap dan pengesahan percubaan dunia sebenar

Pemerolehan data saintifik adalah mahal dan memakan masa, dan model yang hanya dinilai pada set data bebas tidak boleh secara langsung mencerminkan maklum balas daripada dunia sebenar. Kepentingan bagaimana untuk mencapai paradigma eksperimen berulang model-realiti yang cekap serupa dengan GNoME (yang menyepadukan saluran paip hujung ke hujung termasuk latihan rangkaian graf, pengiraan teori fungsi ketumpatan dan makmal automatik untuk penemuan dan sintesis bahan) akan Ia akan meningkat setiap hari. hari.

3. Integrasi dengan Model Bahasa Besar (LLM)

Model Bahasa Besar (LLM) telah terbukti secara meluas mempunyai pengetahuan yang kaya, meliputi pelbagai bidang. Walaupun terdapat beberapa kerja yang menggunakan LLM untuk tugas tertentu, seperti ramalan sifat molekul dan reka bentuk ubat, ia hanya beroperasi pada primitif atau graf molekul. Cara menggabungkannya secara organik dengan rangkaian neural graf geometri supaya mereka boleh memproses maklumat struktur 3D dan melakukan ramalan atau penjanaan pada struktur 3D masih agak mencabar.

4. Kelonggaran kekangan kesetaraan

Tidak syak lagi bahawa kesetaraan adalah penting untuk meningkatkan kecekapan data dan keupayaan generalisasi model, tetapi perlu diperhatikan bahawa kekangan kesetaraan yang terlalu kuat kadangkala boleh menjejaskan modelnya prestasi. Oleh itu, bagaimana untuk mengimbangi kesetaraan dan kebolehsuaian model yang direka bentuk adalah persoalan yang sangat menarik. Penerokaan dalam bidang ini bukan sahaja dapat memperkayakan pemahaman kita tentang tingkah laku model, tetapi juga membuka jalan untuk pembangunan penyelesaian yang lebih mantap dan umum dengan kebolehgunaan yang lebih luas.

Rujukan

[1] Schütt K, Kindermans P J, Sauceda Felix H E, et al: Rangkaian saraf konvolusi penapis berterusan untuk memodelkan interaksi kuantum [J]. .

[2] Satorras V G, Hoogeboom E, Welling M. E (n) rangkaian neural graf setara[C]//Persidangan antarabangsa mengenai pembelajaran mesin. PMLR, 2021: 9323-9332.

[3] Thomas N, Smidt T, Kearnes S, et al. Rangkaian medan tensor: Rangkaian neural setara putaran dan terjemahan untuk awan titik 3d[J]. pracetak arXiv arXiv:1802.08219, 2018.

[4] Gasteiger J, Groß J, Günnemann S. Mesej Arah Lulus untuk Graf Molekul[C]//Persidangan Antarabangsa mengenai Perwakilan Pembelajaran. 2019.

[5] Gasteiger J, Becker F, Günnemann S. Gemnet: Rangkaian neural graf arah universal untuk molekul[J]. Kemajuan dalam Sistem Pemprosesan Maklumat Neural, 2021, 34: 6790-6802.

[6] Pedagang A, Batzner S, Schoenholz S S, et al. Menskalakan pembelajaran mendalam untuk penemuan bahan[J]. Alam Semula Jadi, 2023, 624(7990): 80-85.

Atas ialah kandungan terperinci Asas AI4Science: rangkaian neural graf geometri, semakan paling komprehensif ada di sini! Renmin University of China Hillhouse mengeluarkan bersama makmal AI Tencent, Universiti Tsinghua, Stanford, dsb.. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!