Siswazah kelas Tsinghua Yao menerbitkan dua karya berturut-turut, peningkatan terbesar dalam sepuluh tahun: pendaraban matriks hampir dengan teori optimum

Dengan menghapuskan "ketidakcekapan tersembunyi", saintis komputer telah menghasilkan cara baharu untuk mendarab matriks besar lebih cepat berbanding sebelum ini.

Sebagai operasi asas banyak pengendali GPU, pendaraban matriks memainkan peranan penting dalam pengkomputeran berprestasi tinggi dan juga merupakan komponen utama aplikasi seperti AI. Walaupun algoritma itu sendiri agak mudah, usaha telah dilakukan untuk mengoptimumkannya selama bertahun-tahun untuk mencapai kelajuan yang lebih tinggi. Walau bagaimanapun, tahap pengoptimuman agak terhad.

Dalam keluaran terbaru Majalah Kuantum, kami menemui dua kertas kerja yang boleh mempercepatkan pendaraban matriks. Dalam penulisan kedua-dua kertas kerja ini, seorang pelajar sarjana kanan dari Kelas Yao di Universiti Tsinghua mengambil bahagian secara aktif, yang membawa prospek baharu untuk penambahbaikan algoritma dalam bidang ini.

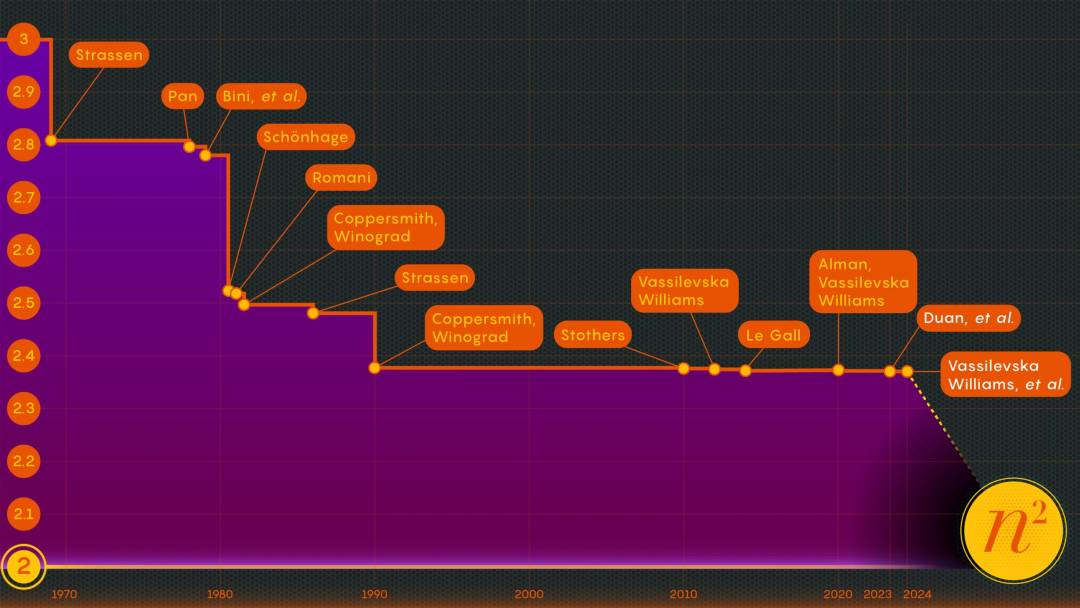
Satu "singulariti" baharu muncul dalam penambahbaikan pendaraban matriks

Saintis komputer adalah kumpulan manusia yang sangat menuntut. Apa yang mereka kejar bukan sahaja menyelesaikan masalah, tetapi juga mencapai matlamat dengan cara yang paling berkesan.

Ambil contoh mendarab matriks atau tatasusunan nombor Pada tahun 1812, ahli matematik Perancis Jacques Philippe Marie Binet mencadangkan satu set peraturan asas yang masih diajar kepada pelajar hari ini. Set peraturan ini digunakan secara meluas, tetapi dalam beberapa tahun kebelakangan ini beberapa ahli matematik telah menemui cara untuk memudahkan dan mempercepatkan proses. Ahli matematik Perancis Jacques Philippe Marie Binet.

Pada masa ini, mempercepatkan proses pendaraban matriks telah menjadi persimpangan matematik dan sains komputer. Penyelidik telah berusaha untuk memperbaiki proses ini, walaupun kemajuan telah terhad dalam beberapa dekad kebelakangan ini. François Le Gall, seorang saintis komputer di Universiti Nagoya, menunjukkan bahawa penambahbaikan berangka kepada pendaraban matriks telah perlahan dan sukar difahami sejak 1987. Beliau percaya bahawa dalam keadaan semasa, meningkatkan lagi kecekapan pendaraban matriks menghadapi cabaran besar dan memerlukan lebih banyak inovasi dan kejayaan. Walaupun menghadapi kesukaran, saintis masih berusaha tanpa mengenal penat lelah untuk mencari penemuan, berharap untuk mencari kaedah dan teknik baharu untuk meningkatkan kelajuan pengiraan dan kecekapan pendaraban matriks. Ini menunjukkan bahawa pengoptimuman pendaraban matriks masih menjadi topik yang mencabar dan memerlukan usaha kolektif

Ran Duan dan Renfei Zhou dari Universiti Tsinghua dan Hongxun Wu dari University of California, Berkeley, untuk menyelesaikan masalah yang telah lama wujud ini dibuat, dan hasil penyelidikan mereka dibentangkan secara terperinci dalam kertas setebal 87 muka surat. Le Gall memuji kerja ketiga-tiga penyelidik ini. Kertas kerja ini telah diterima oleh FOCS 2023, persidangan teratas dalam bidang sains komputer.

Paper v1 akan dikeluarkan pada Oktober 2022, v5 pada November 2023. Alamat kertas: https://arxiv.org/abs/2210.10173

Antaranya, Duan Ran ialah profesor bersekutu di Institut Maklumat Silang di Universiti Tsinghua Arah penyelidikan utamanya ialah algoritma teori graf, struktur data dan pengkomputeran teori. Hongxun Wu ialah pelajar kedoktoran tahun kedua di University of California, Berkeley, dan lulusan Kelas Yao Universiti Tsinghua.

Zhou Renfei ialah pelajar sarjana kanan dalam Kelas Yao 2020 di Universiti Tsinghua, pengkhususan dalam Sains Komputer Teori (TCS). Beliau bekerja terutamanya pada struktur data (ringkas) dan pendaraban matriks yang cepat, dan mempunyai minat yang luas dalam bidang TCS yang lain seperti algoritma penstriman, teori permainan dan algoritma dalam talian.

Sebelum ini, Zhou Renfei telah menerbitkan banyak kertas kerja di FOCS/SODA, persidangan sains komputer teoretikal teratas.

Kerja oleh tiga penyelidik mendedahkan sumber potensi penambahbaikan yang tidak diketahui sebelum ini dan belum diterokai yang sudah membuahkan hasil. Kertas kerja kedua yang diterbitkan pada Januari 2024 (juga dikarang bersama oleh Renfei Zhou) membina ini dan menunjukkan cara pendaraban matriks boleh dipertingkatkan lagi.

Alamat kertas: https://epubs.siam.org/doi/10.1137/1.9781611977912.134

William Kuszmaul, seorang saintis komputer teoritis di Universiti Harvard, lebih banyak mengatakan bahawa ini adalah kejayaan besar di Universiti Harvard. Peningkatan terbesar yang telah kami lihat dalam beberapa tahun untuk pendaraban matriks.

Apakah masalah yang perlu diperbaiki dalam pendaraban matriks

Pendaraban matriks mungkin kelihatan seperti masalah yang tidak jelas, tetapi ia adalah operasi pengiraan asas. Ia digabungkan ke dalam kebanyakan algoritma yang digunakan orang setiap hari untuk pelbagai tugas, daripada memaparkan grafik komputer yang lebih jelas kepada menyelesaikan masalah logistik dalam teori rangkaian. Sama seperti dalam bidang pengkomputeran lain, kelajuan adalah penting. Malah penambahbaikan kecil akhirnya boleh mengurangkan masa, kuasa pengkomputeran dan wang yang diperlukan dengan ketara. Tetapi buat masa ini, ahli teori terutamanya berminat untuk memikirkan betapa pantas proses itu boleh berjalan.

Kaedah tradisional untuk mendarab dua n×n matriks—iaitu, mendarab nombor dalam setiap baris matriks pertama dengan nombor dalam setiap lajur matriks kedua—memerlukan n³ operasi pendaraban bebas. Untuk matriks 2 dengan 2, ini bermakna 2³, atau 8 pendaraban.

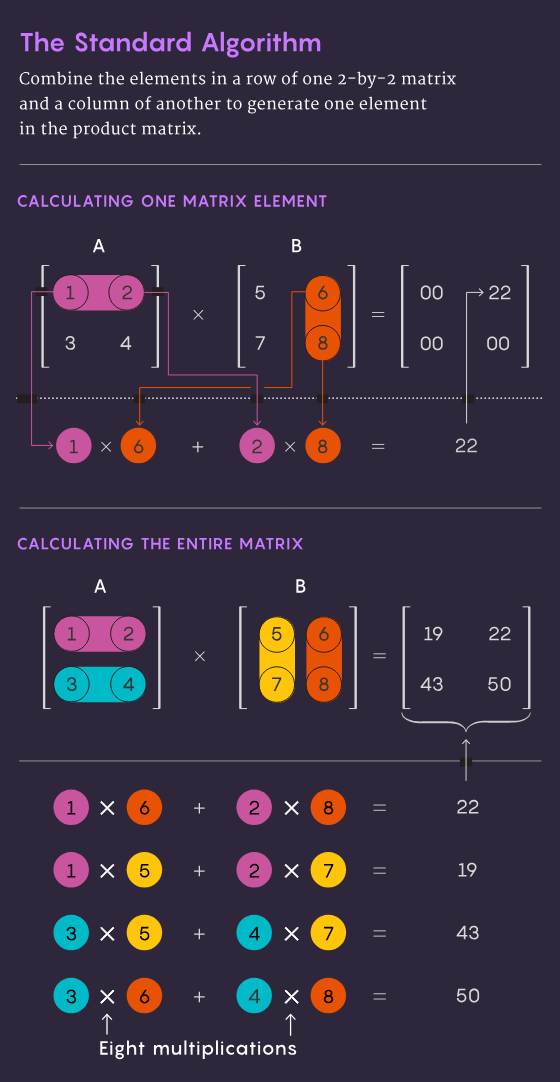
Pada tahun 1969, ahli matematik Volker Strassen menemui kaedah yang lebih elegan yang boleh melengkapkan pendaraban 2×2 matriks hanya dalam 7 langkah pendaraban dan 18 langkah penambahan. Dua tahun kemudian, saintis komputer Shmuel Winograd menunjukkan bahawa pendaraban 7 langkah sememangnya minimum mutlak untuk matriks 2 × 2.

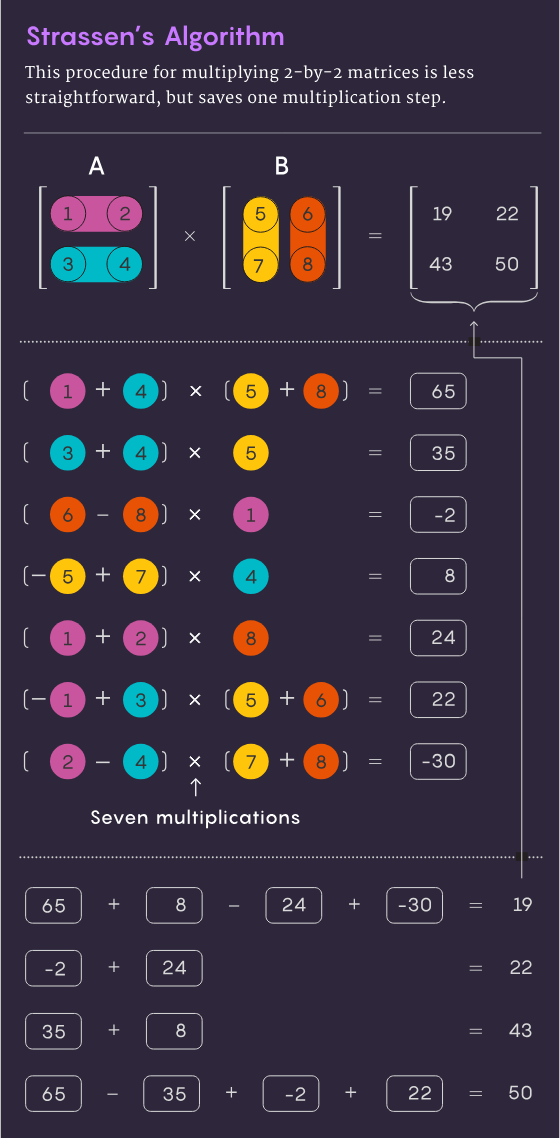
Strassen menggunakan idea yang sama untuk menunjukkan bahawa semua matriks n×n yang lebih besar juga boleh didarab dalam kurang daripada n3 langkah. Elemen utama dalam strategi ini melibatkan prosedur yang dipanggil penguraian: menguraikan matriks besar kepada submatriks yang lebih kecil, yang mungkin menjadi sekecil 2×2 atau 1×1 (hanya satu nombor).

Alasan untuk memecahkan tatasusunan gergasi kepada kepingan kecil adalah agak mudah, seorang saintis komputer di MIT, Virginia Vassilevska Williams, berkata: "Untuk matriks yang besar (seperti matriks 100×100), sukar untuk manusia memikirkannya. algoritma terbaik ” Malah matriks 3 dengan 3 belum diselesaikan sepenuhnya. "Walau bagaimanapun, seseorang boleh menggunakan algoritma pantas yang telah dibangunkan untuk matriks kecil untuk mendapatkan algoritma pantas untuk matriks yang lebih besar

Para penyelidik menentukan bahawa kunci kepada kelajuan adalah untuk mengurangkan bilangan langkah pendaraban, memindahkan eksponen dari n3 sebanyak." mungkin (kaedah tradisional) kurangkan. Nilai n² yang mungkin paling rendah pada asasnya ialah masa yang diperlukan untuk menulis jawapan. Para saintis komputer memanggil eksponen ini Ω, atau ω. nω ialah bilangan langkah minimum yang diperlukan untuk berjaya mendarab dua n×n matriks apabila n semakin besar. Zhou Renfei, yang juga pengarang bersama kertas kerja Januari 2024, berkata: "Tumpuan kerja ini adalah untuk melihat sejauh mana anda boleh mencapai 2 dan sama ada ia boleh dicapai secara teori

Kaedah laser

Pada tahun 1986, Strassen memperoleh Dalam satu lagi kejayaan besar, beliau memperkenalkan kaedah laser pendaraban matriks. Strassen menggunakan ini untuk menentukan nilai sempadan atas untuk ω sebanyak 2.48. Walaupun kaedah itu hanya satu langkah dalam pendaraban matriks besar, ia adalah salah satu yang paling penting kerana penyelidik sentiasa memperbaikinya.

Setahun kemudian, Winograd dan Don Coppersmith memperkenalkan algoritma baharu yang melengkapkan kaedah laser dengan sempurna. Gabungan alat ini digunakan dalam hampir semua penyelidikan seterusnya mengenai mempercepatkan pendaraban matriks.

Berikut ialah cara ringkas untuk melihat cara elemen berbeza ini sesuai bersama. Mari kita mulakan dengan dua matriks besar A dan B dan darabkannya. Mula-mula, anda memecahkannya kepada banyak submatriks yang lebih kecil, kadangkala dipanggil blok. Seterusnya, anda boleh menggunakan algoritma Coppersmith dan Winograd sebagai panduan untuk memproses dan akhirnya memasang blok ini. "Ia memberitahu saya apa yang perlu didarabkan, apa yang perlu ditambah, dan elemen mana yang berada dalam matriks produk C," kata Vassilevska Williams "Ia hanya 'resipi' untuk membina C daripada A dan B."

Walau bagaimanapun, terdapat masalah: kadangkala anda mendapat blok dengan unsur biasa. Mengekalkan elemen biasa ini adalah sama dengan mengira elemen ini dua kali, jadi pada satu ketika, pertindihan ini perlu dihapuskan. Para penyelidik menyelesaikan masalah ini dengan "membunuh" blok yang mereka ada - menetapkan komponen mereka kepada sifar untuk mengeluarkannya daripada pengiraan.

                                                                                                                       ^{pasukan ahli yang menambah baik kaedah pendaraban matriks baharu, dan dia menghasilkan kaedah terpantas pada masa ini.}

Di sinilah kaedah laser Strassen akhirnya dimainkan. "Kaedah laser biasanya sangat berkesan dan sering mencari cara yang baik untuk menghapuskan sub-blok yang bertindih, " kata Le Gall. Selepas laser telah menghapuskan semua pertindihan, anda boleh membina matriks produk akhir C.

Menggabungkan pelbagai teknik ini menghasilkan algoritma yang mendarab dua matriks dengan jumlah pendaraban sesedikit mungkin, sekurang-kurangnya secara teori. Kaedah laser tidak bertujuan untuk aplikasi praktikal; ia hanyalah cara pemikiran yang ideal tentang pendaraban matriks. Zhou Renfei berkata, "Kami tidak pernah menjalankan kaedah ini pada komputer, kami menganalisisnya." Analisis inilah yang telah membawa kepada peningkatan terbesar ω dalam lebih sepuluh tahun.

"Kehilangan tersembunyi" ditemui

Dalam kertas pertama "Pendaraban Matriks Lebih Cepat melalui Pencapaian Asymmetric" oleh Duan Ran, Zhou Renfei dan Hongxun Wu, mereka menunjukkan bahawa proses algoritma Strassen boleh dipercepatkan dengan sangat baik. Ini semua berkat konsep yang mereka panggil "kerugian tersembunyi." Zhou Renfei berkata bahawa konsep itu sangat tersembunyi dalam analisis sebelum ini dan merupakan hasil daripada menghapuskan terlalu banyak blok secara tidak sengaja.

Kaedah laser berfungsi dengan menandakan blok bertindih sebagai sampah dan menjadualkannya untuk diproses, manakala blok lain dianggap berharga dan akan disimpan. Walau bagaimanapun, proses pemilihan agak rawak. Malah, blok yang ditandakan sebagai sampah mungkin berguna.

Ini tidak mengejutkan sepenuhnya, tetapi dengan memeriksa banyak pilihan rawak, pasukan Duan Ran menentukan bahawa kaedah laser secara sistematik meremehkan nilai blok, jadi lebih banyak blok harus disimpan dan kurang dibuang. Dan, seperti yang sering berlaku, kurang sisa diterjemahkan kepada kecekapan yang lebih besar.

Mengenai pendekatan pasukan Duan Ran, Le Gall percaya bahawa "lebih banyak blok boleh dikekalkan tanpa bertindih pendekatan ini mencapai algoritma pendaraban matriks yang lebih pantas

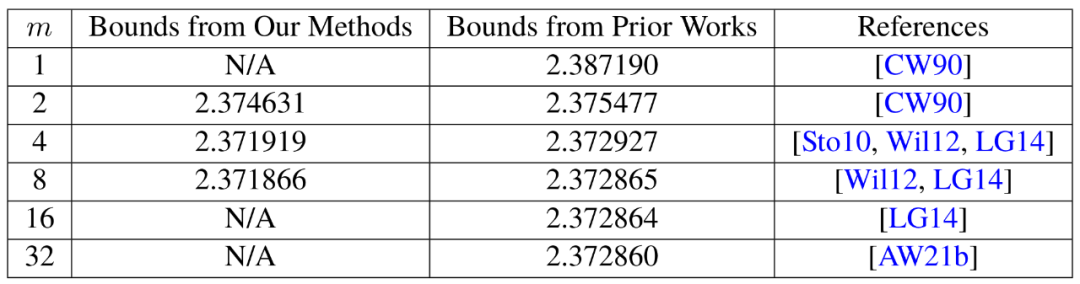
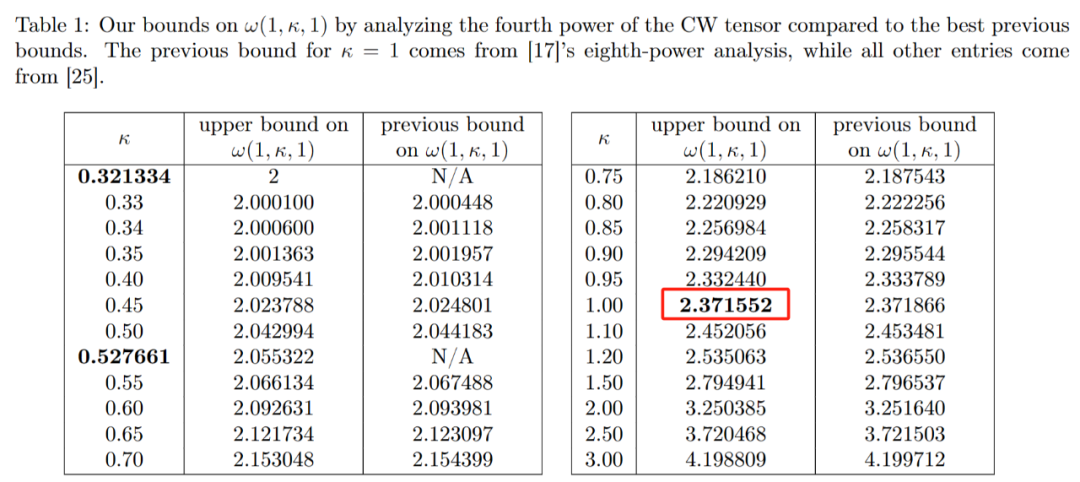
Selepas membuktikan kewujudan kehilangan ini, Duan Ran The pasukan mengubah suai cara laser. kaedah menandakan blok, dengan ketara mengurangkan sisa. Mereka menetapkan had baharu pada ω sekitar 2.371866, iaitu peningkatan berbanding had 2.3728596 yang ditetapkan oleh Josh Alman dan Vassilevska Williams pada tahun 2020.

Ini mungkin kelihatan seperti perubahan kecil,

menurunkan had atas sebanyak kira-kira 0.001, tetapi ia merupakan peningkatan terbesar yang pernah dilihat saintis sejak 2010

. Sebagai perbandingan, keputusan Vassilevska Williams dan Alman 2020 meningkat hanya 0.00001 daripada keputusan sebelumnya.

Sudah tentu, perkara yang paling menggembirakan para penyelidik bukan hanya rekod baharu itu sendiri, yang tidak bertahan lama. Malah, kertas kerja ini mendedahkan jalan baharu untuk penambahbaikan yang sebelum ini tidak disedari sama sekali.

Menurut Le Gall, semua orang telah bergantung pada kaedah laser yang sama selama hampir empat dekad. Dengan kemunculan kertas kerja oleh tiga penyelidik termasuk Duan Ran, kami boleh melakukan yang lebih baik.

Oleh itu, kertas kerja Januari 2024 yang dikarang bersama oleh Zhou Renfei telah menambah baik kaedah baharu ini dan seterusnya mengurangkan kerugian tersembunyi. Mereka meningkatkan lagi had atas ω, menurunkannya kepada 2.371552

.

Penyelidik juga menggunakan kaedah yang sama untuk menambah baik proses pendaraban matriks segi empat tepat (n×m), yang digunakan secara meluas dalam teori graf, pembelajaran mesin dan bidang lain.

Beberapa kemajuan lanjut di sepanjang garis ini hampir pasti, tetapi ada hadnya. Pada tahun 2015, Le Gall dan dua pengarang bersama menunjukkan bahawa kaedah semasa, iaitu kaedah laser, ditambah dengan kaedah Coppersmith dan Winograd, tidak dapat memperoleh ω di bawah 2.3078.

Le Gall berkata: "Jika anda ingin menambah baik lagi, anda perlu menambah baik kaedah asal Coppersmith dan Winograd, yang tidak benar-benar berubah sejak 1987 tetapi setakat ini, tiada siapa yang mencadangkannya. Mungkin tidak sama sekali.

Zhou Renfei berkata: "Memperbaiki ω sebenarnya adalah sebahagian daripada memahami masalah ini. Jika kita dapat memahami masalah ini dengan baik, kita boleh mereka bentuk algoritma yang lebih baik. Walau bagaimanapun, pemahaman orang ramai tentang masalah purba ini masih berada pada Tahap yang sangat asas. 》

Pautan asal:

https://www.quantamagazine.org/new-breakthrough-brings-matrix-multiplication-closer-to-ideal-20240307/

Atas ialah kandungan terperinci Siswazah kelas Tsinghua Yao menerbitkan dua karya berturut-turut, peningkatan terbesar dalam sepuluh tahun: pendaraban matriks hampir dengan teori optimum. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!