Pendaraban matriks universal CUDA: dari kemasukan kepada kemahiran!

Pendaraban Matriks Umum (GEMM) ialah bahagian penting dalam banyak aplikasi dan algoritma, dan juga merupakan salah satu petunjuk penting untuk menilai prestasi perkakasan komputer. Penyelidikan mendalam dan pengoptimuman pelaksanaan GEMM boleh membantu kami lebih memahami pengkomputeran berprestasi tinggi dan hubungan antara perisian dan sistem perkakasan. Dalam sains komputer, pengoptimuman GEMM yang berkesan boleh meningkatkan kelajuan pengkomputeran dan menjimatkan sumber, yang penting untuk meningkatkan prestasi keseluruhan sistem komputer. Pemahaman yang mendalam tentang prinsip kerja dan kaedah pengoptimuman GEMM akan membantu kami menggunakan potensi perkakasan pengkomputeran moden dengan lebih baik dan menyediakan penyelesaian yang lebih cekap untuk pelbagai tugas pengkomputeran yang kompleks. Dengan mengoptimumkan dan meningkatkan prestasi GEMM, kita boleh menambah

1. Ciri-ciri asas GEMM

1.1 Proses pengiraan GEMM dan kerumitan

GEMM ditakrifkan sebagai

. untuk ketepatan

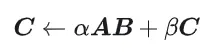
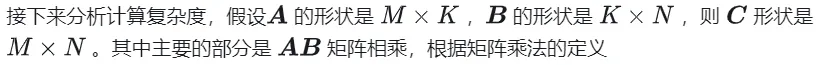
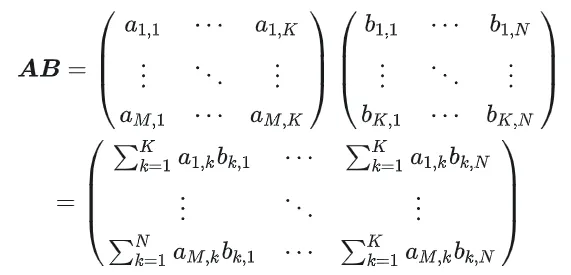
#define OFFSET(row, col, ld) ((row) * (ld) + (col))void cpuSgemm(float *a, float *b, float *c, const int M, const int N, const int K) {for (int m = 0; m <p style="text-align: center;">Yang berikut menggunakan CUDA untuk melaksanakan Kernal, pendaraban matriks paling mudah Sebanyak M * N benang digunakan untuk melengkapkan keseluruhan pendaraban matriks. Setiap benang bertanggungjawab untuk pengiraan unsur dalam matriks C dan perlu melengkapkan K kali pendaraban dan pengumpulan. Matriks A, B dan C semuanya disimpan dalam memori global (ditentukan oleh pengubah suai </p> <h4>
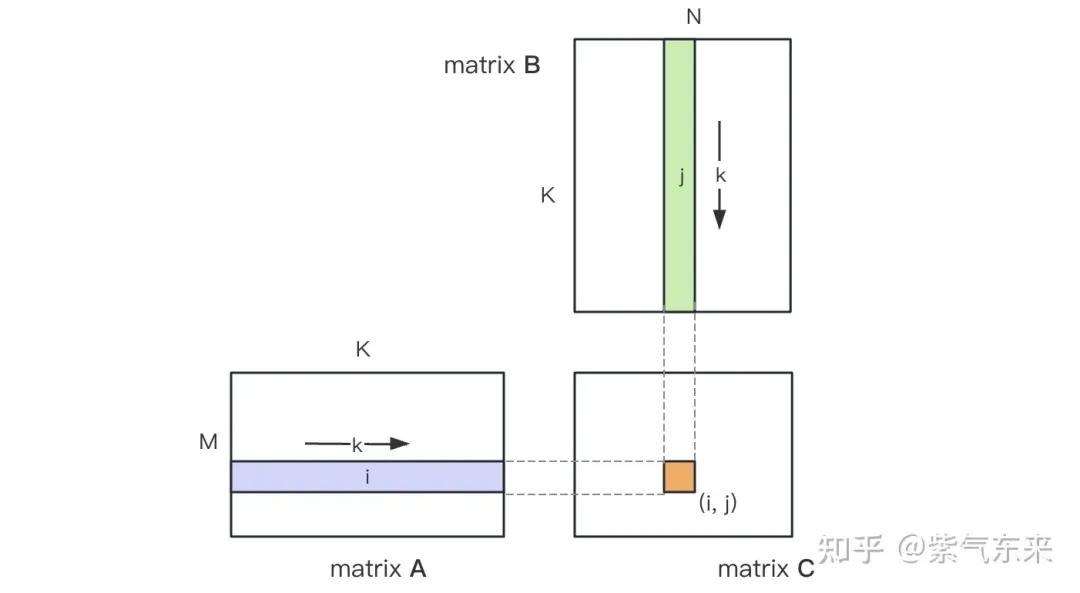
<span></span> </h4> Untuk kod lengkap, lihat sgemm_naive.cu . <p><img src="https://img.php.cn/upload/article/000/465/014/171134103163048.jpg" alt="Pendaraban matriks universal CUDA: dari kemasukan kepada kemahiran!"></p><pre class="brush:php;toolbar:false">__global__ void naiveSgemm(float * __restrict__ a, float * __restrict__ b, float * __restrict__ c,const int M, const int N, const int K) {int n = blockIdx.x * blockDim.x + threadIdx.x;int m = blockIdx.y * blockDim.y + threadIdx.y;if (m <p>Kompilasi selesai, dan hasil pelaksanaan pada Tesla V100-PCIE-32GB adalah seperti berikut Menurut kertas putih V100, kuasa pengkomputeran puncak FP32 ialah 15.7 TFLOPS, jadi penggunaan kuasa pengkomputeran ini. kaedah hanya 11.5%. </p><div><pre class="brush:php;toolbar:false">M N K =128128 1024, Time = 0.00010083 0.00010260 0.00010874 s, AVG Performance = 304.5951 GflopsM N K =192192 1024, Time = 0.00010173 0.00010198 0.00010253 s, AVG Performance = 689.4680 GflopsM N K =256256 1024, Time = 0.00010266 0.00010318 0.00010384 s, AVG Performance =1211.4281 GflopsM N K =384384 1024, Time = 0.00019475 0.00019535 0.00019594 s, AVG Performance =1439.7206 GflopsM N K =512512 1024, Time = 0.00037693 0.00037794 0.00037850 s, AVG Performance =1322.9753 GflopsM N K =768768 1024, Time = 0.00075238 0.00075558 0.00075776 s, AVG Performance =1488.9271 GflopsM N K = 1024 1024 1024, Time = 0.00121562 0.00121669 0.00121789 s, AVG Performance =1643.8068 GflopsM N K = 1536 1536 1024, Time = 0.00273072 0.00275611 0.00280208 s, AVG Performance =1632.7386 GflopsM N K = 2048 2048 1024, Time = 0.00487622 0.00488028 0.00488614 s, AVG Performance =1639.2518 GflopsM N K = 3072 3072 1024, Time = 0.01001603 0.01071136 0.01099990 s, AVG Performance =1680.4589 GflopsM N K = 4096 4096 1024, Time = 0.01771046 0.01792170 0.01803462 s, AVG Performance =1785.5450 GflopsM N K = 6144 6144 1024, Time = 0.03988969 0.03993405 0.04000595 s, AVG Performance =1802.9724 GflopsM N K = 8192 8192 1024, Time = 0.07119219 0.07139694 0.07160816 s, AVG Performance =1792.7940 GflopsM N K =1228812288 1024, Time = 0.15978026 0.15993242 0.16043369 s, AVG Performance =1800.7606 GflopsM N K =1638416384 1024, Time = 0.28559187 0.28567238 0.28573316 s, AVG Performance =1792.2629 Gflops

Yang berikut mengambil M=512, K=512, N=512 sebagai contoh untuk menganalisis aliran kerja proses pengiraan di atas secara terperinci:

1. Dalam Memori Global, peruntukkan ruang storan untuk matriks A, B dan C masing-masing.
2. Oleh kerana matriks Pengiraan setiap elemen dalam C adalah bebas antara satu sama lain, jadi dalam pemetaan selari, setiap utas sepadan dengan pengiraan 1 elemen dalam matriks C.
3. Kedua-dua gridSize dan blockSize dalam konfigurasi pelaksanaan mempunyai x (arah lajur) , y (arah baris) dua dimensi, antaranya

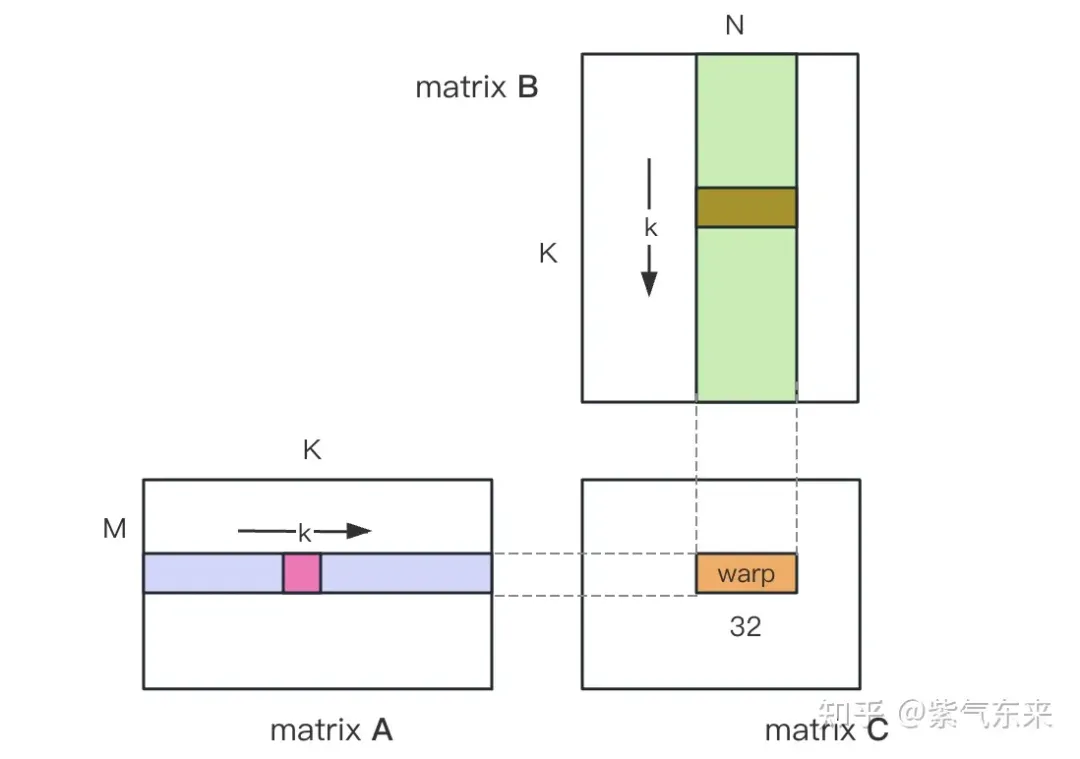
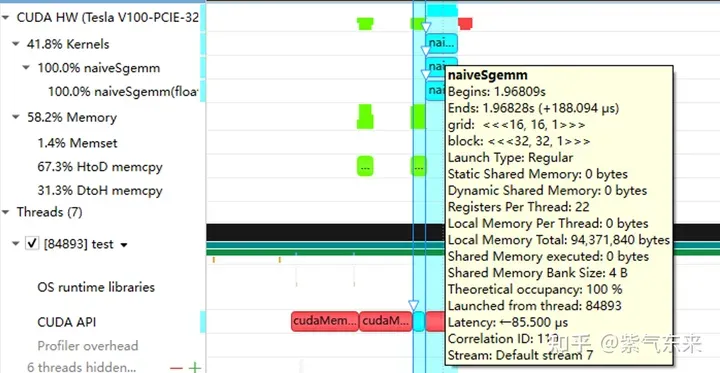
nsys merekodkan versi naif pemprofilan

pemprofilan GE

Yang sebelumnya artikel hanya GEMM berfungsi telah dilaksanakan, tetapi prestasinya jauh dari jangkaan Bahagian ini terutamanya akan mengkaji pengoptimuman prestasi GEMM.

2.1 Pembahagian matriks menggunakan Memori Dikongsi

Pengiraan di atas memerlukan dua beban Memori Global untuk menyelesaikan operasi pendaraban dan pengumpulan Nisbah capaian memori pengiraan adalah sangat rendah, dan tiada penggunaan semula data yang berkesan. Oleh itu, Memori Dikongsi boleh digunakan untuk mengurangkan bacaan memori berulang.

Mula-mula bahagikan matriks C kepada blok yang sama dengan saiz BMxBN Setiap blok dikira oleh Blok, di mana setiap Benang bertanggungjawab untuk mengira elemen TMxTN dalam matriks C. Selepas itu, semua data yang diperlukan untuk pengiraan dibaca daripada smem, yang menghapuskan sebahagian daripada bacaan memori berulang bagi matriks A dan B. Memandangkan Memori Dikongsi mempunyai kapasiti terhad, blok bersaiz BK boleh dibaca dalam dimensi K setiap kali Gelung sedemikian memerlukan jumlah K / BK kali untuk menyelesaikan keseluruhan operasi pendaraban matriks, dan hasil Blok boleh diperolehi. Prosesnya ditunjukkan dalam rajah di bawah:

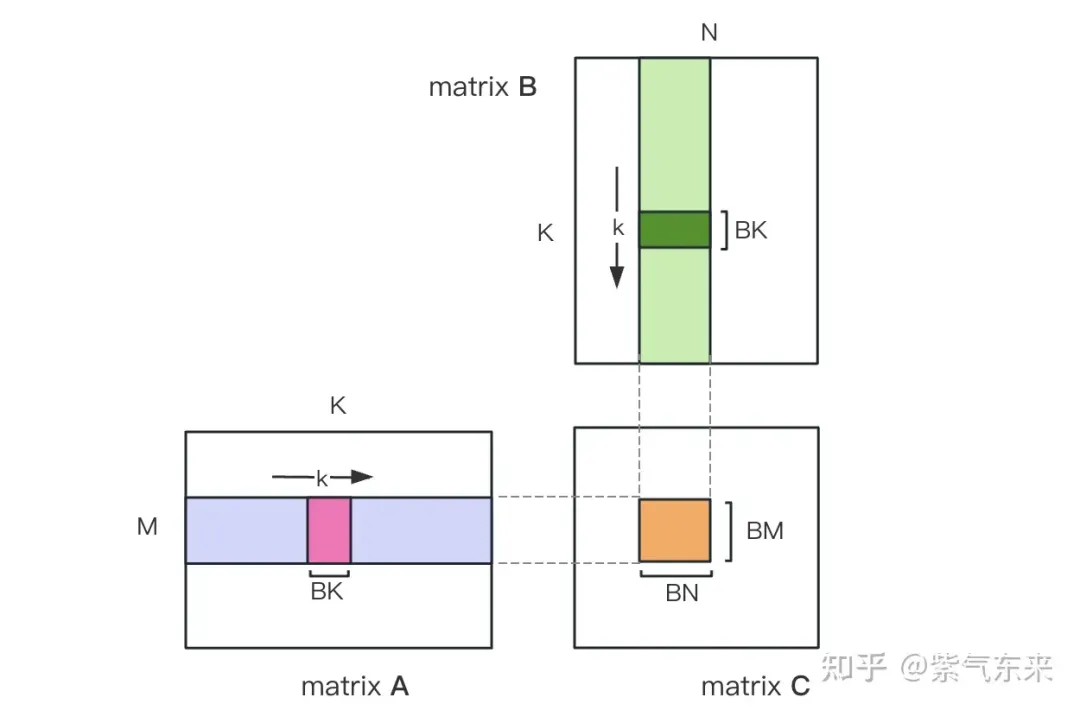
Selepas pengoptimuman menggunakan Shared Memory, bagi setiap blok, kita boleh mendapat:

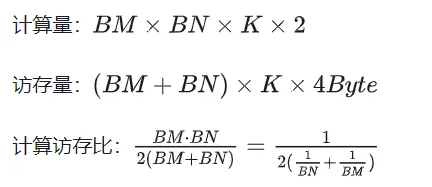
Dapat dilihat daripada formula di atas bahawa semakin besar BM dan BN, semakin besar lebih tinggi nisbah capaian ingatan pengiraan, dan prestasi akan menjadi lebih baik. Walau bagaimanapun, disebabkan oleh had kapasiti Memori Dikongsi (V100 1 SM hanya 96KB), Blok perlu menduduki BK * (BM + BN) * saiz 4 Bait.

Nilai TM dan TN juga dihadkan oleh dua aspek Di satu pihak, terdapat sekatan pada bilangan utas BM / TM * BN / TN dalam satu Blok melebihi 1024, dan tidak boleh terlalu tinggi untuk menghalangnya daripada menjejaskan Keselarian antara blok sebaliknya, terdapat had pada bilangan daftar A memerlukan sekurang-kurangnya daftar TM * TN untuk menyimpan jumlah separa matriks C, ditambah beberapa daftar lain Bilangan semua daftar tidak boleh melebihi 256, dan tidak boleh Terlalu tinggi untuk mengelakkan menjejaskan bilangan utas serentak dalam SM.

Akhir sekali pilih BM = BN = 128, BK = 8, TM = TN = 8, maka nisbah capaian memori yang dikira ialah 32. Mengikut kuasa pengkomputeran teori V100 15.7TFLOPS, kita boleh mendapat 15.7TFLOPS/32 = 490GB/s Mengikut lebar jalur HBM yang diukur ialah 763GB/s, dapat dilihat bahawa lebar jalur tidak lagi akan mengehadkan prestasi pengkomputeran pada masa ini. masa.

Berdasarkan analisis di atas, proses pelaksanaan fungsi kernel adalah seperti berikut Untuk kod lengkap, lihat sgemm_v1.cu Langkah-langkah utama termasuk:

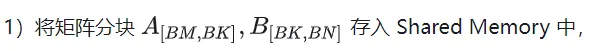
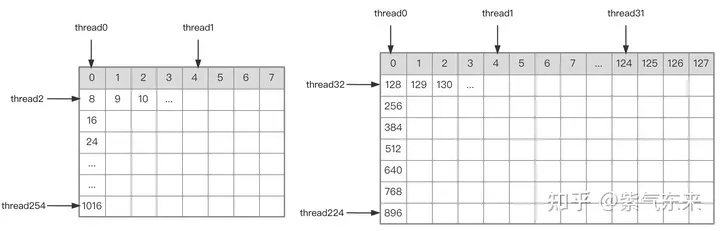
A B Hubungan indeks pembahagian matriks.

确定好单个block的执行过程，接下来需要确定多block处理的不同分块在Global Memory中的对应关系，仍然以A为例进行说明。由于分块沿着行的方向移动，那么首先需要确定行号，根据 Grid 的二维全局线性索引关系，by * BM 表示该分块的起始行号，同时我们已知load_a_smem_m 为分块内部的行号，因此全局的行号为load_a_gmem_m = by * BM + load_a_smem_m 。由于分块沿着行的方向移动，因此列是变化的，需要在循环内部计算，同样也是先计算起始列号bk * BK 加速分块内部列号load_a_smem_k 得到 load_a_gmem_k = bk * BK + load_a_smem_k ，由此我们便可以确定了分块在原始数据中的位置OFFSET(load_a_gmem_m, load_a_gmem_k, K) 。同理可分析矩阵分块 的情况，不再赘述。

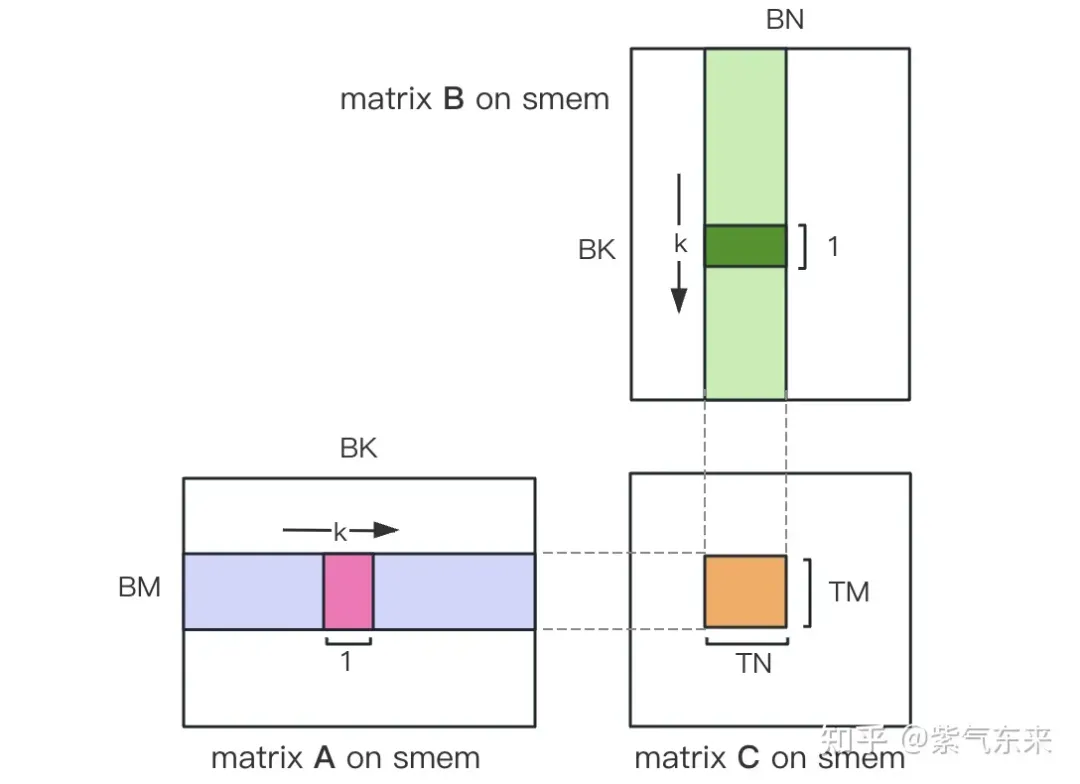
计算完后，还需要将其存入 Global Memory 中，这就需要计算其在 Global Memory 中的对应关系。由于存在更小的分块，则行和列均由3部分构成：全局行号store_c_gmem_m 等于大分块的起始行号by * BM+小分块的起始行号ty * TM+小分块内部的相对行号 i 。列同理。

__global__ void sgemm_V1(float * __restrict__ a, float * __restrict__ b, float * __restrict__ c,const int M, const int N, const int K) {const int BM = 128;const int BN = 128;const int BK = 8;const int TM = 8;const int TN = 8;const int bx = blockIdx.x;const int by = blockIdx.y;const int tx = threadIdx.x;const int ty = threadIdx.y;const int tid = ty * blockDim.x + tx;__shared__ float s_a[BM][BK];__shared__ float s_b[BK][BN];float r_c[TM][TN] = {0.0};int load_a_smem_m = tid >> 1;// tid/2, row of s_aint load_a_smem_k = (tid & 1) > 5; // tid/32, row of s_bint load_b_smem_n = (tid & 31) 

计算结果如下，性能达到了理论峰值性能的51.7%：

M N K =128128 1024, Time = 0.00031578 0.00031727 0.00032288 s, AVG Performance =98.4974 GflopsM N K =192192 1024, Time = 0.00031638 0.00031720 0.00031754 s, AVG Performance = 221.6661 GflopsM N K =256256 1024, Time = 0.00031488 0.00031532 0.00031606 s, AVG Performance = 396.4287 GflopsM N K =384384 1024, Time = 0.00031686 0.00031814 0.00032080 s, AVG Performance = 884.0425 GflopsM N K =512512 1024, Time = 0.00031814 0.00032007 0.00032493 s, AVG Performance =1562.1563 GflopsM N K =768768 1024, Time = 0.00032397 0.00034419 0.00034848 s, AVG Performance =3268.5245 GflopsM N K = 1024 1024 1024, Time = 0.00034570 0.00034792 0.00035331 s, AVG Performance =5748.3952 GflopsM N K = 1536 1536 1024, Time = 0.00068797 0.00068983 0.00069094 s, AVG Performance =6523.3424 GflopsM N K = 2048 2048 1024, Time = 0.00136173 0.00136552 0.00136899 s, AVG Performance =5858.5604 GflopsM N K = 3072 3072 1024, Time = 0.00271910 0.00273115 0.00274006 s, AVG Performance =6590.6331 GflopsM N K = 4096 4096 1024, Time = 0.00443805 0.00445964 0.00446883 s, AVG Performance =7175.4698 GflopsM N K = 6144 6144 1024, Time = 0.00917891 0.00950608 0.00996963 s, AVG Performance =7574.0999 GflopsM N K = 8192 8192 1024, Time = 0.01628838 0.01645271 0.01660790 s, AVG Performance =7779.8733 GflopsM N K =1228812288 1024, Time = 0.03592557 0.03597434 0.03614323 s, AVG Performance =8005.7066 GflopsM N K =1638416384 1024, Time = 0.06304122 0.06306373 0.06309302 s, AVG Performance =8118.7715 Gflops

下面仍以M=512,K=512,N=512为例，分析一下结果。首先通过 profiling 可以看到 Shared Memory 占用为 8192 bytes，这与理论上(128+128)X8X4完全一致。

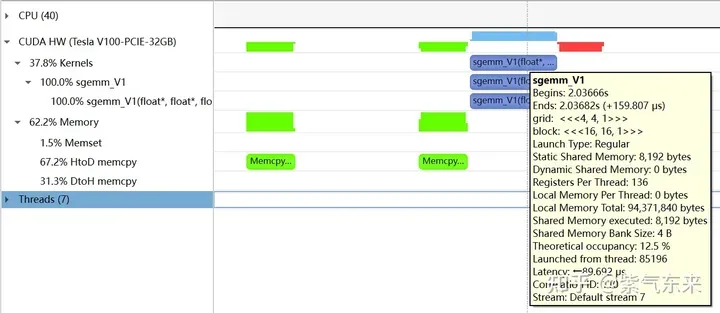nsys 记录 的 V1 版本的 profiling

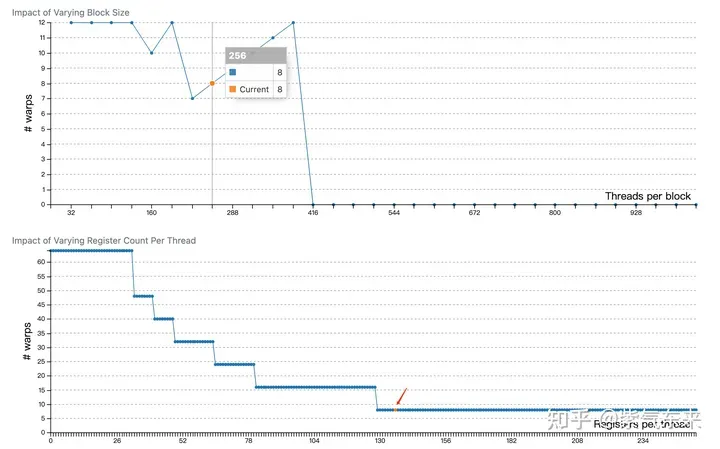
profiling 显示 Occupancy 为 12.5%，可以通过 cuda-calculator 加以印证，该例中 threads per block = 256, Registers per thread = 136, 由此可以计算得到每个SM中活跃的 warp 为8，而对于V100，每个SM中的 warp 总数为64，因此 Occupancy 为 8/64 = 12.5%。

2.2 解决 Bank Conflict 问题

上节通过利用 Shared Memory 大幅提高了访存效率，进而提高了性能，本节将进一步优化 Shared Memory 的使用。

Shared Memory一共划分为32个Bank，每个Bank的宽度为4 Bytes，如果需要访问同一个Bank的多个数据，就会发生Bank Conflict。例如一个Warp的32个线程，如果访问的地址分别为0、4、8、...、124，就不会发生Bank Conflict，只占用Shared Memory一拍的时间；如果访问的地址为0、8、16、...、248，这样一来地址0和地址128对应的数据位于同一Bank、地址4和地址132对应的数据位于同一Bank，以此类推，那么就需要占用Shared Memory两拍的时间才能读出。

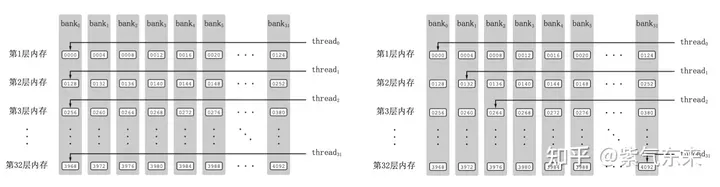
有 Bank Conflict VS 无 Bank Conflict

再看 V1 版本计算部分的三层循环，每次从Shared memory中取矩阵A的长度为TM的向量和矩阵B的长度为TN的向量，这两个向量做外积并累加到部分和中，一次外积共TM * TN次乘累加，一共需要循环BK次取数和外积。

接下来分析从Shared Memory load的过程中存在的Bank Conflict：

i) 取矩阵A需要取一个列向量，而矩阵A在Shared Memory中是按行存储的；

ii) 在TM = TN = 8的情况下，无论矩阵A还是矩阵B，从Shared Memory中取数时需要取连续的8个数，即便用LDS.128指令一条指令取四个数，也需要两条指令，由于一个线程的两条load指令的地址是连续的，那么同一个Warp不同线程的同一条load指令的访存地址就是被间隔开的，便存在着 Bank Conflict。

为了解决上述的两点Shared Memory的Bank Conflict，采用了一下两点优化：

i) 为矩阵A分配Shared Memory时形状分配为[BK][BM]，即让矩阵A在Shared Memory中按列存储

ii) 将原本每个线程负责计算的TM * TN的矩阵C，划分为下图中这样的两块TM/2 * TN的矩阵C，由于TM/2=4，一条指令即可完成A的一块的load操作，两个load可同时进行。

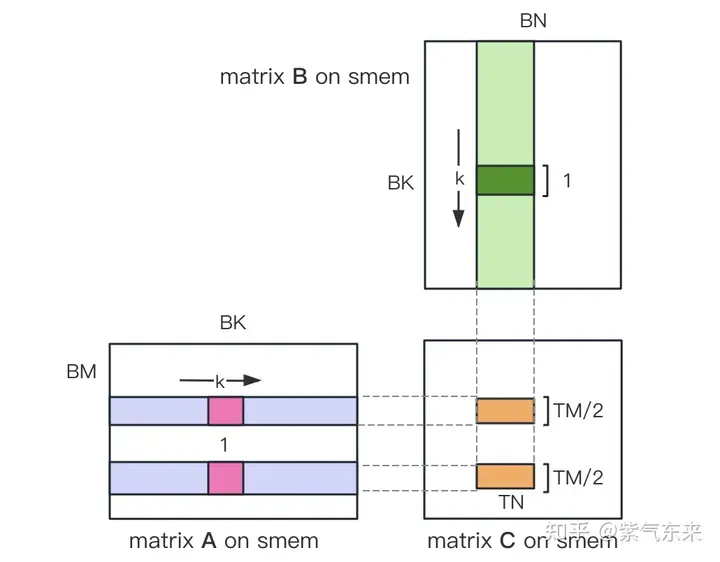
kernel 函数的核心部分实现如下，完整代码见 sgemm_v2.cu 。

__shared__ float s_a[BK][BM];__shared__ float s_b[BK][BN];float r_load_a[4];float r_load_b[4];float r_comp_a[TM];float r_comp_b[TN];float r_c[TM][TN] = {0.0};int load_a_smem_m = tid >> 1;int load_a_smem_k = (tid & 1) > 5;int load_b_smem_n = (tid & 31) 

结果如下，相对未解决 Bank Conflict 版(V1) 性能提高了 14.4%，达到了理论峰值的74.3%。

M N K =128128 1024, Time = 0.00029699 0.00029918 0.00030989 s, AVG Performance = 104.4530 GflopsM N K =192192 1024, Time = 0.00029776 0.00029828 0.00029882 s, AVG Performance = 235.7252 GflopsM N K =256256 1024, Time = 0.00029485 0.00029530 0.00029619 s, AVG Performance = 423.2949 GflopsM N K =384384 1024, Time = 0.00029734 0.00029848 0.00030090 s, AVG Performance = 942.2843 GflopsM N K =512512 1024, Time = 0.00029853 0.00029945 0.00030070 s, AVG Performance =1669.7479 GflopsM N K =768768 1024, Time = 0.00030458 0.00032467 0.00032790 s, AVG Performance =3465.1038 GflopsM N K = 1024 1024 1024, Time = 0.00032406 0.00032494 0.00032621 s, AVG Performance =6155.0281 GflopsM N K = 1536 1536 1024, Time = 0.00047990 0.00048224 0.00048461 s, AVG Performance =9331.3912 GflopsM N K = 2048 2048 1024, Time = 0.00094426 0.00094636 0.00094992 s, AVG Performance =8453.4569 GflopsM N K = 3072 3072 1024, Time = 0.00187866 0.00188096 0.00188538 s, AVG Performance =9569.5816 GflopsM N K = 4096 4096 1024, Time = 0.00312589 0.00319050 0.00328147 s, AVG Performance = 10029.7885 GflopsM N K = 6144 6144 1024, Time = 0.00641280 0.00658940 0.00703498 s, AVG Performance = 10926.6372 GflopsM N K = 8192 8192 1024, Time = 0.01101130 0.01116194 0.01122950 s, AVG Performance = 11467.5446 GflopsM N K =1228812288 1024, Time = 0.02464854 0.02466705 0.02469344 s, AVG Performance = 11675.4946 GflopsM N K =1638416384 1024, Time = 0.04385955 0.04387468 0.04388355 s, AVG Performance = 11669.5995 Gflops

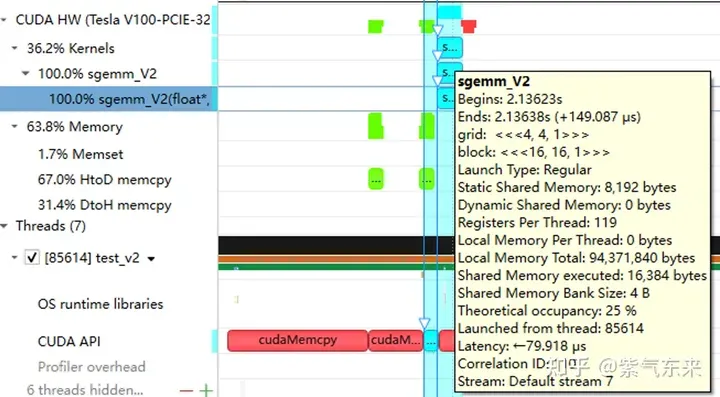
分析一下 profiling 可以看到 Static Shared Memory 仍然是使用了8192 Bytes，奇怪的的是，Shared Memory executed 却翻倍变成了 16384 Bytes（知友如果知道原因可以告诉我一下）。

2.3 流水并行化：Double Buffering

Double Buffering，即双缓冲，即通过增加buffer的方式，使得 访存-计算 的串行模式流水线化，以减少等待时间，提高计算效率，其原理如下图所示:

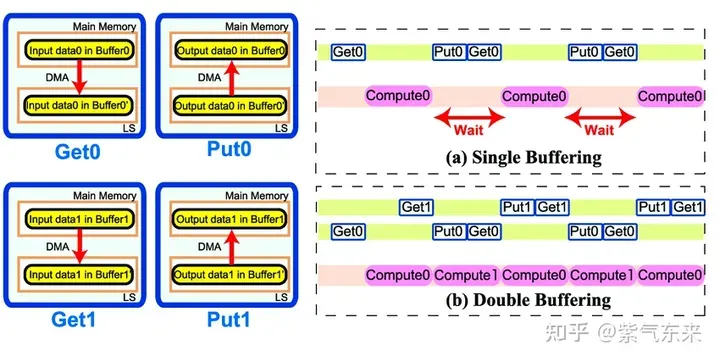
Single Buffering VS Double Buffering

具体到 GEMM 任务中来，就是需要两倍的Shared Memory，之前只需要BK * (BM + BN) * 4 Bytes的Shared Memory，采用Double Buffering之后需要2BK * (BM + BN) * 4 Bytes的Shared Memory，然后使其 pipeline 流动起来。

代码核心部分如下所示，完整代码参见 sgemm_v3.cu 。有以下几点需要注意：

1）主循环从bk = 1 开始，第一次数据加载在主循环之前，最后一次计算在主循环之后，这是pipeline 的特点决定的；

2）由于计算和下一次访存使用的Shared Memory不同，因此主循环中每次循环只需要一次__syncthreads()即可

3）由于GPU不能向CPU那样支持乱序执行，主循环中需要先将下一次循环计算需要的Gloabal Memory中的数据load 到寄存器，然后进行本次计算，之后再将load到寄存器中的数据写到Shared Memory，这样在LDG指令向Global Memory做load时，不会影响后续FFMA及其它运算指令的 launch 执行，也就达到了Double Buffering的目的。

__shared__ float s_a[2][BK][BM];__shared__ float s_b[2][BK][BN];float r_load_a[4];float r_load_b[4];float r_comp_a[TM];float r_comp_b[TN];float r_c[TM][TN] = {0.0};int load_a_smem_m = tid >> 1;int load_a_smem_k = (tid & 1) > 5;int load_b_smem_n = (tid & 31) 

性能如下所示，达到了理论峰值的 80.6%。

M N K =128128 1024, Time = 0.00024000 0.00024240 0.00025792 s, AVG Performance = 128.9191 GflopsM N K =192192 1024, Time = 0.00024000 0.00024048 0.00024125 s, AVG Performance = 292.3840 GflopsM N K =256256 1024, Time = 0.00024029 0.00024114 0.00024272 s, AVG Performance = 518.3728 GflopsM N K =384384 1024, Time = 0.00024070 0.00024145 0.00024198 s, AVG Performance =1164.8394 GflopsM N K =512512 1024, Time = 0.00024173 0.00024237 0.00024477 s, AVG Performance =2062.9786 GflopsM N K =768768 1024, Time = 0.00024291 0.00024540 0.00026010 s, AVG Performance =4584.3820 GflopsM N K = 1024 1024 1024, Time = 0.00024534 0.00024631 0.00024941 s, AVG Performance =8119.7302 GflopsM N K = 1536 1536 1024, Time = 0.00045712 0.00045780 0.00045872 s, AVG Performance =9829.5167 GflopsM N K = 2048 2048 1024, Time = 0.00089632 0.00089970 0.00090656 s, AVG Performance =8891.8924 GflopsM N K = 3072 3072 1024, Time = 0.00177891 0.00178289 0.00178592 s, AVG Performance = 10095.9883 GflopsM N K = 4096 4096 1024, Time = 0.00309763 0.00310057 0.00310451 s, AVG Performance = 10320.6843 GflopsM N K = 6144 6144 1024, Time = 0.00604826 0.00619887 0.00663078 s, AVG Performance = 11615.0253 GflopsM N K = 8192 8192 1024, Time = 0.01031738 0.01045051 0.01048861 s, AVG Performance = 12248.2036 GflopsM N K =1228812288 1024, Time = 0.02283978 0.02285837 0.02298272 s, AVG Performance = 12599.3212 GflopsM N K =1638416384 1024, Time = 0.04043287 0.04044823 0.04046151 s, AVG Performance = 12658.1556 Gflops

从 profiling 可以看到双倍的 Shared Memory 的占用

三、cuBLAS 实现方式探究

本节我们将认识CUDA的标准库——cuBLAS， 即NVIDIA版本的基本线性代数子程序 (Basic Linear Algebra Subprograms, BLAS) 规范实现代码。它支持 Level 1 (向量与向量运算) ，Level 2 (向量与矩阵运算) ，Level 3 (矩阵与矩阵运算) 级别的标准矩阵运算。

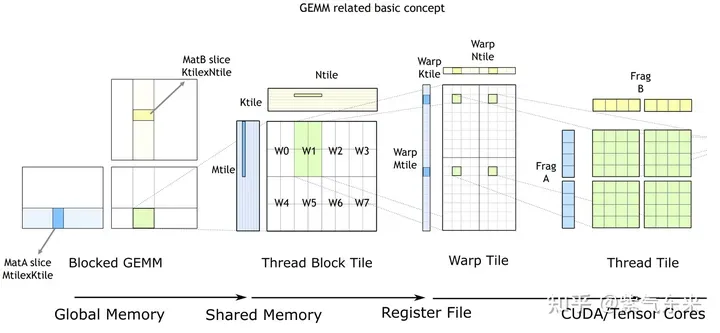
cuBLAS/CUTLASS GEMM的基本过程

如上图所示，计算过程分解成线程块片（thread block tile）、线程束片（warp tile）和线程片（thread tile）的层次结构并将AMP的策略应用于此层次结构来高效率的完成基于GPU的拆分成tile的GEMM。这个层次结构紧密地反映了NVIDIA CUDA编程模型。可以看到从global memory到shared memory的数据移动（矩阵到thread block tile）；从shared memory到寄存器的数据移动（thread block tile到warp tile）；从寄存器到CUDA core的计算（warp tile到thread tile）。

cuBLAS 实现了单精度矩阵乘的函数cublasSgemm，其主要参数如下：

cublasStatus_t cublasSgemm( cublasHandle_t handle, // 调用 cuBLAS 库时的句柄 cublasOperation_t transa, // A 矩阵是否需要转置 cublasOperation_t transb, // B 矩阵是否需要转置 int m, // A 的行数 int n, // B 的列数 int k, // A 的列数 const float *alpha, // 系数 α, host or device pointer const float *A, // 矩阵 A 的指针，device pointer int lda, // 矩阵 A 的主维，if A 转置， lda = max(1, k), else max(1, m) const float *B, // 矩阵 B 的指针, device pointer int ldb, // 矩阵 B 的主维，if B 转置， ldb = max(1, n), else max(1, k) const float *beta, // 系数 β, host or device pointer float *C, // 矩阵 C 的指针，device pointer int ldc // 矩阵 C 的主维，ldc >= max(1, m) );

调用方式如下：

cublasHandle_t cublas_handle;cublasCreate(&cublas_handle);float cublas_alpha = 1.0;float cublas_beta = 0;cublasSgemm(cublas_handle, CUBLAS_OP_N, CUBLAS_OP_N, N, M, K, &cublas_alpha, d_b, N, d_a, K, &cublas_beta, d_c, N);

性能如下所示，达到了理论峰值的 82.4%。

M N K =128128 1024, Time = 0.00002704 0.00003634 0.00010822 s, AVG Performance = 860.0286 GflopsM N K =192192 1024, Time = 0.00003155 0.00003773 0.00007267 s, AVG Performance =1863.6689 GflopsM N K =256256 1024, Time = 0.00003917 0.00004524 0.00007747 s, AVG Performance =2762.9438 GflopsM N K =384384 1024, Time = 0.00005318 0.00005978 0.00009120 s, AVG Performance =4705.0655 GflopsM N K =512512 1024, Time = 0.00008326 0.00010280 0.00013840 s, AVG Performance =4863.9646 GflopsM N K =768768 1024, Time = 0.00014278 0.00014867 0.00018816 s, AVG Performance =7567.1560 GflopsM N K = 1024 1024 1024, Time = 0.00023485 0.00024460 0.00028150 s, AVG Performance =8176.5614 GflopsM N K = 1536 1536 1024, Time = 0.00046474 0.00047607 0.00051181 s, AVG Performance =9452.3201 GflopsM N K = 2048 2048 1024, Time = 0.00077930 0.00087862 0.00092307 s, AVG Performance =9105.2126 GflopsM N K = 3072 3072 1024, Time = 0.00167904 0.00168434 0.00171114 s, AVG Performance = 10686.6837 GflopsM N K = 4096 4096 1024, Time = 0.00289619 0.00291068 0.00295904 s, AVG Performance = 10994.0128 GflopsM N K = 6144 6144 1024, Time = 0.00591766 0.00594586 0.00596915 s, AVG Performance = 12109.2611 GflopsM N K = 8192 8192 1024, Time = 0.01002384 0.01017465 0.01028435 s, AVG Performance = 12580.2896 GflopsM N K =1228812288 1024, Time = 0.02231159 0.02233805 0.02245619 s, AVG Performance = 12892.7969 GflopsM N K =1638416384 1024, Time = 0.03954650 0.03959291 0.03967242 s, AVG Performance = 12931.6086 Gflops

由此可以对比以上各种方法的性能情况，可见手动实现的性能已接近于官方的性能，如下：

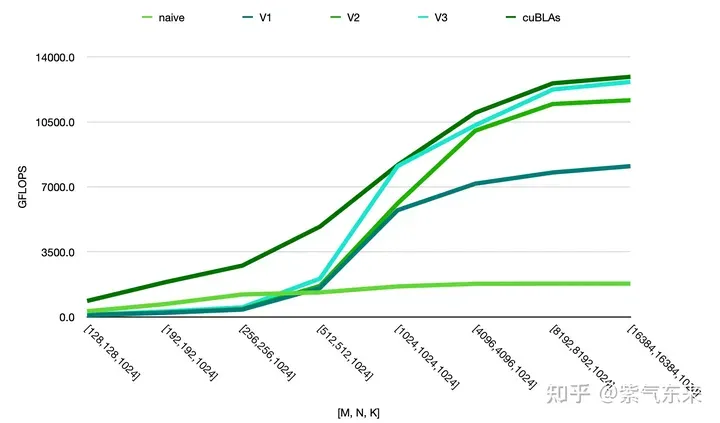
Atas ialah kandungan terperinci Pendaraban matriks universal CUDA: dari kemasukan kepada kemahiran!. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!