 Peranti teknologi
Peranti teknologi
 AI
AI
 Pendaftaran awan titik tidak dapat dielakkan untuk penglihatan 3D! Fahami semua penyelesaian dan cabaran arus perdana dalam satu artikel
Pendaftaran awan titik tidak dapat dielakkan untuk penglihatan 3D! Fahami semua penyelesaian dan cabaran arus perdana dalam satu artikel
Pendaftaran awan titik tidak dapat dielakkan untuk penglihatan 3D! Fahami semua penyelesaian dan cabaran arus perdana dalam satu artikel
Awan titik sebagai koleksi mata dijangka membawa perubahan dalam mendapatkan dan menjana maklumat permukaan tiga dimensi (3D) objek melalui pembinaan semula 3D, pemeriksaan industri dan operasi robot. Proses yang paling mencabar tetapi penting ialah pendaftaran awan titik, iaitu mendapatkan transformasi spatial yang menjajarkan dan memadankan dua awan titik yang diperoleh dalam dua koordinat berbeza. Kajian ini memperkenalkan gambaran keseluruhan dan prinsip asas pendaftaran awan titik, mengklasifikasikan dan membandingkan pelbagai kaedah secara sistematik, dan menyelesaikan masalah teknikal yang wujud dalam pendaftaran awan titik, cuba menyediakan penyelidik akademik di luar lapangan dan Jurutera memberikan bimbingan dan memudahkan perbincangan mengenai visi bersatu untuk pendaftaran awan titik.
Kaedah umum pemerolehan awan titik
dibahagikan kepada kaedah aktif dan pasif Awan titik yang diperoleh secara aktif oleh penderia ialah kaedah aktif, dan kaedah melalui pembinaan semula pada peringkat seterusnya ialah kaedah pasif.
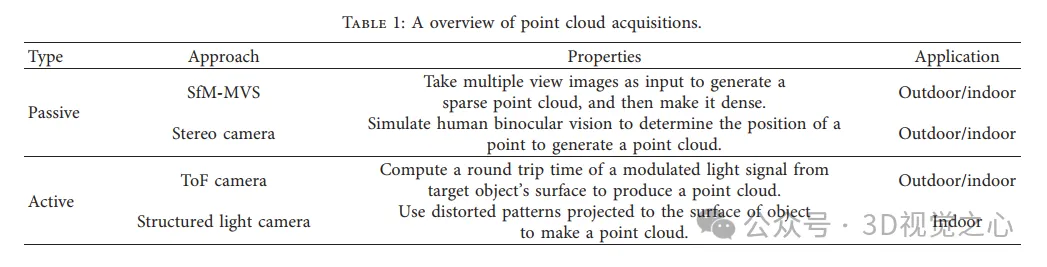
Pembinaan semula padat daripada SFM kepada MVS. (a) SFM. (b) Contoh awan titik yang dihasilkan oleh SfM. (c) Carta aliran algoritma PMVS, algoritma stereo berbilang paparan berasaskan tampalan. (d) Contoh awan titik tumpat yang dihasilkan oleh PMVS.
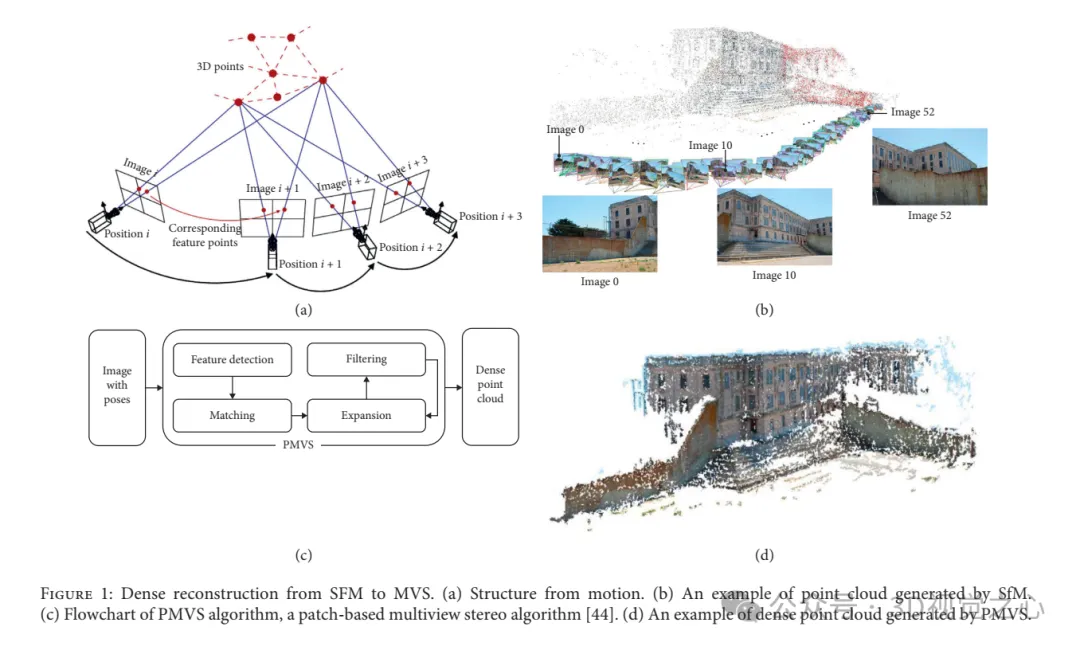
Kaedah Pembinaan Lampu Berstruktur: Pendaftaran dan pendaftaran yang tidak tegar dalam persekitaran, transformasi boleh diuraikan ke dalam putaran dan terjemahan. awan titik lain sambil mengekalkan bentuk dan saiz yang sama.
Dalam pendaftaran tidak tegar, transformasi tidak tegar diwujudkan untuk membungkus data yang diimbas ke awan titik sasaran. Transformasi tidak tegar termasuk pantulan, putaran, penskalaan dan terjemahan, berbanding hanya terjemahan dan putaran dalam pendaftaran tegar. Pendaftaran tidak tegar digunakan untuk dua sebab utama: (1) ralat tak linear dan penentukuran dalam pemerolehan data boleh menyebabkan herotan frekuensi rendah imbasan objek tegar (2) pendaftaran dilakukan pada pemandangan atau objek yang berubah bentuk dan bergerak mengikut masa . 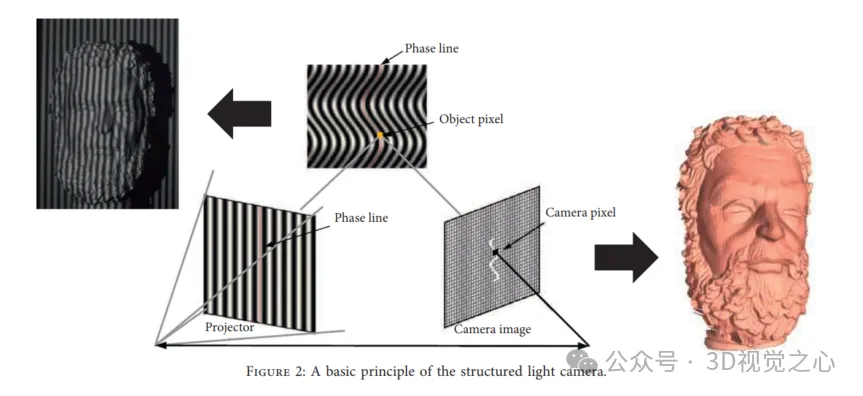
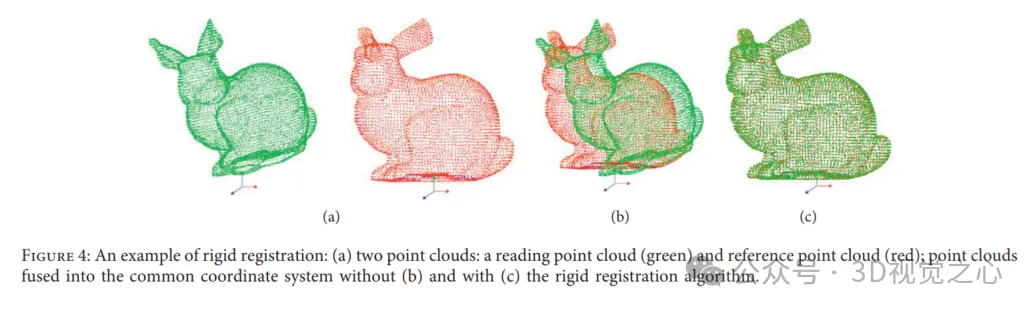
Contoh pendaftaran tegar: (a) awan dua titik: awan titik baca (hijau) dan awan titik rujukan (merah); ke dalam sistem koordinat biasa.
Walau bagaimanapun, prestasi pendaftaran awan titik dihadkan oleh Varian Overlap, hingar dan outlier, kos pengiraan yang tinggi dan pelbagai petunjuk kejayaan pendaftaran. 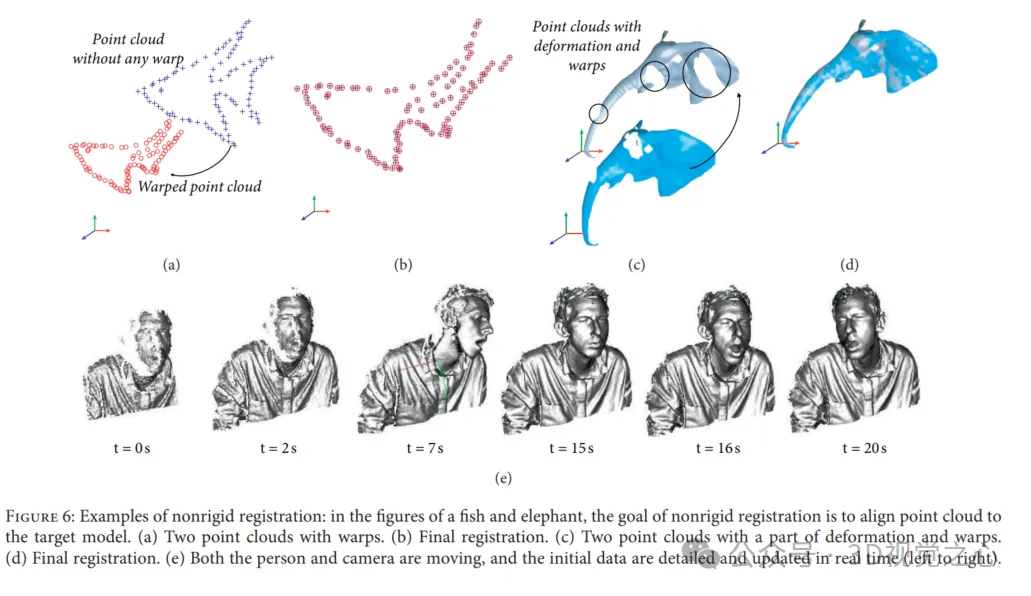
Apakah kaedah pendaftaran?
 Dalam beberapa dekad yang lalu, semakin banyak kaedah pendaftaran awan titik telah dicadangkan, daripada algoritma ICP klasik kepada penyelesaian yang digabungkan dengan teknologi pembelajaran mendalam.
Dalam beberapa dekad yang lalu, semakin banyak kaedah pendaftaran awan titik telah dicadangkan, daripada algoritma ICP klasik kepada penyelesaian yang digabungkan dengan teknologi pembelajaran mendalam. 
1) Skim ICP
Algoritma ICP ialah algoritma berulang yang boleh memastikan ketepatan, kelajuan penumpuan dan kestabilan pendaftaran di bawah keadaan yang ideal. Dari satu segi, ICP boleh dilihat sebagai masalah pemaksimuman jangkaan (EM), jadi ia mengira dan mengemas kini transformasi baharu berdasarkan surat-menyurat, yang kemudiannya digunakan pada data baca sehingga metrik ralat menumpu. Walau bagaimanapun, ini tidak menjamin bahawa ICP mencapai optimum global Algoritma ICP boleh dibahagikan secara kasar kepada empat langkah: pemilihan titik, pemadanan titik, penolakan titik dan pengecilan metrik ralat seperti yang ditunjukkan dalam rajah di bawah.
2) Kaedah berasaskan ciri
Seperti yang kita lihat dalam algoritma berasaskan ICP, adalah penting untuk mewujudkan surat-menyurat sebelum mengubah anggaran. Keputusan akhir dijamin jika kami memperoleh surat-menyurat yang sesuai yang menerangkan hubungan yang betul antara dua awan titik. Oleh itu, kita boleh menampal tanda tempat pada sasaran yang diimbas, atau memilih pasangan mata setara secara manual dalam pemprosesan pasca untuk mengira transformasi tempat menarik (mata terpilih), yang akhirnya boleh digunakan untuk membaca awan titik. Seperti yang ditunjukkan dalam Rajah 12(c), awan titik dimuatkan dalam sistem koordinat yang sama dan dilukis dalam warna yang berbeza. Rajah 12(a) dan 12(b) menunjukkan dua awan titik ditangkap pada sudut pandangan yang berbeza, dengan pasangan titik dipilih daripada data rujukan dan membaca data masing-masing, dan keputusan pendaftaran ditunjukkan dalam Rajah 12(d). Walau bagaimanapun, kaedah ini tidak mesra objek pengukuran yang tidak boleh dilampirkan tanda tempat, dan tidak boleh digunakan pada aplikasi yang memerlukan pendaftaran automatik. Pada masa yang sama, untuk meminimumkan ruang carian surat-menyurat dan mengelakkan andaian transformasi awal dalam algoritma berasaskan ICP, pendaftaran berasaskan ciri diperkenalkan, di mana perkara utama yang direka oleh penyelidik diekstrak. Biasanya, pengesanan titik utama dan penubuhan surat-menyurat adalah langkah utama kaedah ini.

Kaedah biasa untuk pengekstrakan titik utama termasuk PFH, SHOT, dll. Ia juga penting untuk mereka bentuk algoritma untuk membuang outlier dan menganggarkan transformasi berdasarkan inlier dengan berkesan.
3) Pendekatan berasaskan pembelajaran
Dalam aplikasi yang menggunakan awan titik sebagai input, strategi tradisional untuk menganggar deskriptor ciri sangat bergantung pada sifat geometri unik objek dalam awan titik. Walau bagaimanapun, data dunia sebenar selalunya khusus sasaran dan mungkin mengandungi satah, outlier dan hingar. Tambahan pula, ketidakpadanan yang dialih keluar selalunya mengandungi maklumat berguna yang boleh digunakan untuk pembelajaran. Teknik berasaskan pembelajaran boleh disesuaikan untuk mengekod maklumat semantik dan boleh digeneralisasikan merentas tugasan tertentu. Kebanyakan strategi pendaftaran yang disepadukan dengan teknik pembelajaran mesin adalah lebih pantas dan lebih mantap daripada kaedah klasik, dan secara fleksibel diperluaskan kepada tugas lain seperti anggaran pose objek dan klasifikasi objek. Begitu juga, cabaran utama dalam pendaftaran awan titik berasaskan pembelajaran ialah cara mengekstrak ciri yang tidak berubah-ubah kepada variasi spatial awan titik dan lebih mantap kepada hingar dan outlier.
Wakil kaedah berasaskan pembelajaran ialah: PointNet, PointNet++, PCRNet, Deep Global Registration, Deep Closest Point, Partial Registration Network, Robust Point Matching, PointNetLK, 3DRegNet.
4) Kaedah dengan fungsi ketumpatan kebarangkalian
Pendaftaran awan titik berdasarkan fungsi ketumpatan kebarangkalian (PDF) menjadikan pendaftaran menggunakan model statistik masalah yang dikaji dengan baik Idea utama kaedah ini adalah menggunakan fungsi ketumpatan kebarangkalian khusus mewakili data, seperti Model Campuran Gaussian (GMM) dan Taburan Normal (ND). Tugas pendaftaran dirumuskan semula sebagai masalah menjajarkan dua pengagihan yang sepadan, diikuti dengan fungsi objektif yang mengukur dan meminimumkan perbezaan statistik antara mereka. Pada masa yang sama, disebabkan oleh perwakilan PDF, awan titik boleh dilihat sebagai pengedaran dan bukannya banyak titik individu, jadi ia mengelakkan anggaran surat-menyurat dan mempunyai prestasi anti-bunyi yang baik, tetapi secara amnya lebih perlahan daripada berasaskan ICP kaedah.
5) Kaedah lain
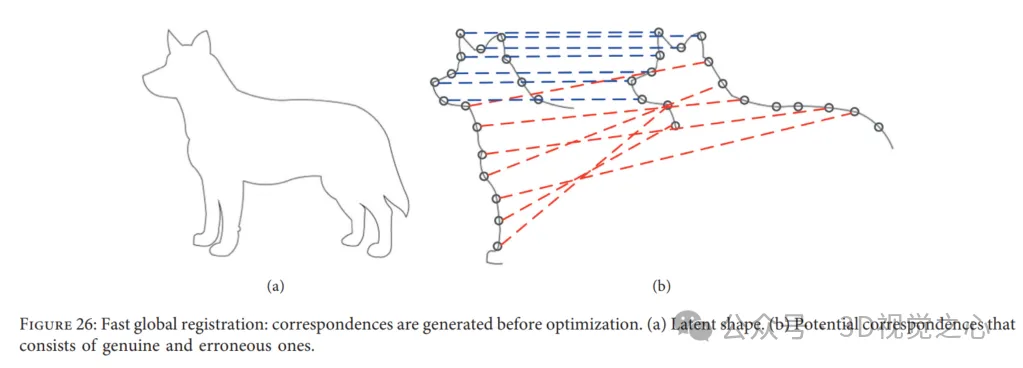
Pendaftaran Global Pantas. Pendaftaran Global Pantas (FGR) menyediakan strategi pantas untuk pendaftaran awan titik tanpa permulaan. Khususnya, FGR beroperasi pada padanan calon permukaan berbumbung dan tidak melakukan pengemaskinian surat-menyurat atau pertanyaan titik terdekat Apa yang istimewa tentang pendekatan ini ialah ia boleh dihasilkan secara langsung oleh pengoptimuman tunggal bagi satu objektif teguh yang ditakrifkan pada permukaan pendaftaran. Walau bagaimanapun, kaedah sedia ada untuk menyelesaikan pendaftaran awan titik biasanya menjana calon atau berbilang surat-menyurat antara dua awan titik dan kemudian mengira dan mengemas kini keputusan global. Tambahan pula, dalam pendaftaran global yang pantas, surat-menyurat diwujudkan serta-merta dalam pengoptimuman dan tidak dianggarkan lagi dalam langkah-langkah berikut. Oleh itu, carian jiran terdekat yang mahal dielakkan untuk memastikan kos pengiraan rendah. Hasilnya, pemprosesan linear untuk setiap surat-menyurat dalam langkah lelaran dan sistem linear untuk anggaran pose adalah cekap. FGR dinilai pada berbilang set data, seperti penanda aras UWA dan Stanford Bunny, berbanding dengan ICP point-to-point dan point-top, dan varian ICP seperti Go ICP. Eksperimen menunjukkan bahawa FGR berfungsi dengan baik dalam kehadiran bunyi!
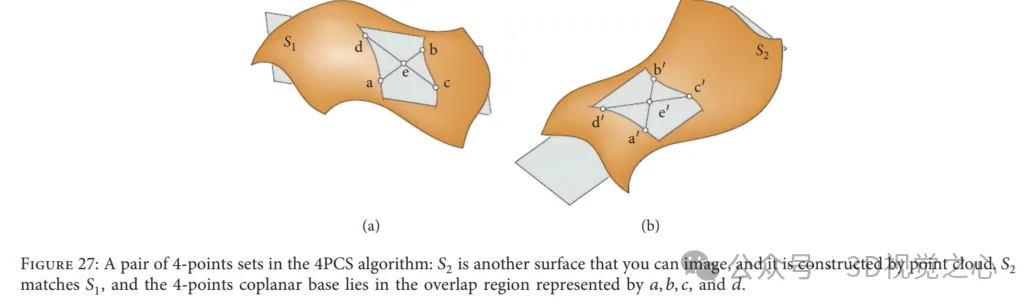
Algoritma set kongruen empat mata: Set kongruen 4 mata (4PCS) menyediakan transformasi awal untuk membaca data tanpa memerlukan andaian kedudukan permulaan. Lazimnya, transformasi pendaftaran tegar antara dua awan titik boleh ditakrifkan secara unik oleh sepasang tiga kali ganda, satu daripada data rujukan dan satu lagi daripada data yang dibaca. Walau bagaimanapun, dalam kaedah ini, ia mencari pangkalan 4 mata khas dengan mencari dalam set potensi kecil, iaitu, 4 titik kongruen koplanar dalam setiap awan titik, seperti yang ditunjukkan dalam Rajah 27. Menyelesaikan transformasi tegar optimum dalam set masalah titik sepunya (LCP) terbesar. Algoritma ini mencapai prestasi rapat apabila pertindihan awan titik berpasangan adalah rendah dan outlier hadir. Untuk menyesuaikan diri dengan aplikasi yang berbeza, ramai penyelidik telah memperkenalkan kerja yang lebih penting berkaitan dengan penyelesaian 4PCS klasik.
Atas ialah kandungan terperinci Pendaftaran awan titik tidak dapat dielakkan untuk penglihatan 3D! Fahami semua penyelesaian dan cabaran arus perdana dalam satu artikel. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!

Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

AI Hentai Generator
Menjana ai hentai secara percuma.

Artikel Panas

Alat panas

Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma

SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan

Hantar Studio 13.0.1
Persekitaran pembangunan bersepadu PHP yang berkuasa

Dreamweaver CS6
Alat pembangunan web visual

SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)

Topik panas
 1378
1378
 52
52
 Mengapakah Gaussian Splatting begitu popular dalam pemanduan autonomi sehingga NeRF mula ditinggalkan?
Jan 17, 2024 pm 02:57 PM
Mengapakah Gaussian Splatting begitu popular dalam pemanduan autonomi sehingga NeRF mula ditinggalkan?
Jan 17, 2024 pm 02:57 PM
Ditulis di atas & pemahaman peribadi pengarang Gaussiansplatting tiga dimensi (3DGS) ialah teknologi transformatif yang telah muncul dalam bidang medan sinaran eksplisit dan grafik komputer dalam beberapa tahun kebelakangan ini. Kaedah inovatif ini dicirikan oleh penggunaan berjuta-juta Gaussians 3D, yang sangat berbeza daripada kaedah medan sinaran saraf (NeRF), yang terutamanya menggunakan model berasaskan koordinat tersirat untuk memetakan koordinat spatial kepada nilai piksel. Dengan perwakilan adegan yang eksplisit dan algoritma pemaparan yang boleh dibezakan, 3DGS bukan sahaja menjamin keupayaan pemaparan masa nyata, tetapi juga memperkenalkan tahap kawalan dan pengeditan adegan yang tidak pernah berlaku sebelum ini. Ini meletakkan 3DGS sebagai penukar permainan yang berpotensi untuk pembinaan semula dan perwakilan 3D generasi akan datang. Untuk tujuan ini, kami menyediakan gambaran keseluruhan sistematik tentang perkembangan dan kebimbangan terkini dalam bidang 3DGS buat kali pertama.
 Ketahui tentang emoji Fasih 3D dalam Microsoft Teams
Apr 24, 2023 pm 10:28 PM
Ketahui tentang emoji Fasih 3D dalam Microsoft Teams
Apr 24, 2023 pm 10:28 PM
Anda mesti ingat, terutamanya jika anda adalah pengguna Teams, bahawa Microsoft telah menambah kumpulan baharu emoji 3DFluent pada apl persidangan video tertumpu kerjanya. Selepas Microsoft mengumumkan emoji 3D untuk Pasukan dan Windows tahun lepas, proses itu sebenarnya telah melihat lebih daripada 1,800 emoji sedia ada dikemas kini untuk platform. Idea besar ini dan pelancaran kemas kini emoji 3DFluent untuk Pasukan pertama kali dipromosikan melalui catatan blog rasmi. Kemas kini Pasukan Terkini membawa FluentEmojis ke aplikasi Microsoft mengatakan 1,800 emoji yang dikemas kini akan tersedia kepada kami setiap hari
 Pilih kamera atau lidar? Kajian terbaru tentang mencapai pengesanan objek 3D yang mantap
Jan 26, 2024 am 11:18 AM
Pilih kamera atau lidar? Kajian terbaru tentang mencapai pengesanan objek 3D yang mantap
Jan 26, 2024 am 11:18 AM
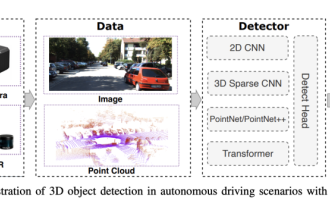
0. Ditulis di hadapan&& Pemahaman peribadi bahawa sistem pemanduan autonomi bergantung pada persepsi lanjutan, membuat keputusan dan teknologi kawalan, dengan menggunakan pelbagai penderia (seperti kamera, lidar, radar, dll.) untuk melihat persekitaran sekeliling dan menggunakan algoritma dan model untuk analisis masa nyata dan membuat keputusan. Ini membolehkan kenderaan mengenali papan tanda jalan, mengesan dan menjejaki kenderaan lain, meramalkan tingkah laku pejalan kaki, dsb., dengan itu selamat beroperasi dan menyesuaikan diri dengan persekitaran trafik yang kompleks. Teknologi ini kini menarik perhatian meluas dan dianggap sebagai kawasan pembangunan penting dalam pengangkutan masa depan satu. Tetapi apa yang menyukarkan pemanduan autonomi ialah memikirkan cara membuat kereta itu memahami perkara yang berlaku di sekelilingnya. Ini memerlukan algoritma pengesanan objek tiga dimensi dalam sistem pemanduan autonomi boleh melihat dan menerangkan dengan tepat objek dalam persekitaran sekeliling, termasuk lokasinya,
 Di luar ORB-SLAM3! SL-SLAM: Adegan bertekstur lemah ringan, kegelisahan teruk dan lemah semuanya dikendalikan
May 30, 2024 am 09:35 AM
Di luar ORB-SLAM3! SL-SLAM: Adegan bertekstur lemah ringan, kegelisahan teruk dan lemah semuanya dikendalikan
May 30, 2024 am 09:35 AM
Ditulis sebelum ini, hari ini kita membincangkan bagaimana teknologi pembelajaran mendalam boleh meningkatkan prestasi SLAM berasaskan penglihatan (penyetempatan dan pemetaan serentak) dalam persekitaran yang kompleks. Dengan menggabungkan kaedah pengekstrakan ciri dalam dan pemadanan kedalaman, di sini kami memperkenalkan sistem SLAM visual hibrid serba boleh yang direka untuk meningkatkan penyesuaian dalam senario yang mencabar seperti keadaan cahaya malap, pencahayaan dinamik, kawasan bertekstur lemah dan seks yang teruk. Sistem kami menyokong berbilang mod, termasuk konfigurasi monokular, stereo, monokular-inersia dan stereo-inersia lanjutan. Selain itu, ia juga menganalisis cara menggabungkan SLAM visual dengan kaedah pembelajaran mendalam untuk memberi inspirasi kepada penyelidikan lain. Melalui percubaan yang meluas pada set data awam dan data sampel sendiri, kami menunjukkan keunggulan SL-SLAM dari segi ketepatan kedudukan dan keteguhan penjejakan.
 CLIP-BEVFormer: Selia secara eksplisit struktur BEVFormer untuk meningkatkan prestasi pengesanan ekor panjang
Mar 26, 2024 pm 12:41 PM
CLIP-BEVFormer: Selia secara eksplisit struktur BEVFormer untuk meningkatkan prestasi pengesanan ekor panjang
Mar 26, 2024 pm 12:41 PM
Ditulis di atas & pemahaman peribadi penulis: Pada masa ini, dalam keseluruhan sistem pemanduan autonomi, modul persepsi memainkan peranan penting Hanya selepas kenderaan pemanduan autonomi yang memandu di jalan raya memperoleh keputusan persepsi yang tepat melalui modul persepsi boleh Peraturan hiliran dan. modul kawalan dalam sistem pemanduan autonomi membuat pertimbangan dan keputusan tingkah laku yang tepat pada masanya dan betul. Pada masa ini, kereta dengan fungsi pemanduan autonomi biasanya dilengkapi dengan pelbagai penderia maklumat data termasuk penderia kamera pandangan sekeliling, penderia lidar dan penderia radar gelombang milimeter untuk mengumpul maklumat dalam modaliti yang berbeza untuk mencapai tugas persepsi yang tepat. Algoritma persepsi BEV berdasarkan penglihatan tulen digemari oleh industri kerana kos perkakasannya yang rendah dan penggunaan mudah, dan hasil keluarannya boleh digunakan dengan mudah untuk pelbagai tugas hiliran.
 Cat 3D dalam Windows 11: Muat Turun, Pemasangan dan Panduan Penggunaan
Apr 26, 2023 am 11:28 AM
Cat 3D dalam Windows 11: Muat Turun, Pemasangan dan Panduan Penggunaan
Apr 26, 2023 am 11:28 AM
Apabila gosip mula tersebar bahawa Windows 11 baharu sedang dibangunkan, setiap pengguna Microsoft ingin tahu bagaimana rupa sistem pengendalian baharu itu dan apa yang akan dibawanya. Selepas spekulasi, Windows 11 ada di sini. Sistem pengendalian datang dengan reka bentuk baharu dan perubahan fungsi. Selain beberapa tambahan, ia disertakan dengan penamatan dan pengalihan keluar ciri. Salah satu ciri yang tidak wujud dalam Windows 11 ialah Paint3D. Walaupun ia masih menawarkan Paint klasik, yang bagus untuk laci, doodle dan doodle, ia meninggalkan Paint3D, yang menawarkan ciri tambahan yang sesuai untuk pencipta 3D. Jika anda mencari beberapa ciri tambahan, kami mengesyorkan Autodesk Maya sebagai perisian reka bentuk 3D terbaik. suka
 Dapatkan isteri 3D maya dalam masa 30 saat dengan satu kad! Teks kepada 3D menjana manusia digital berketepatan tinggi dengan butiran liang yang jelas, menyambung dengan lancar dengan Maya, Unity dan alat pengeluaran lain
May 23, 2023 pm 02:34 PM
Dapatkan isteri 3D maya dalam masa 30 saat dengan satu kad! Teks kepada 3D menjana manusia digital berketepatan tinggi dengan butiran liang yang jelas, menyambung dengan lancar dengan Maya, Unity dan alat pengeluaran lain
May 23, 2023 pm 02:34 PM
ChatGPT telah menyuntik satu dos darah ayam ke dalam industri AI, dan segala-galanya yang dahulunya tidak dapat dibayangkan telah menjadi amalan asas hari ini. Text-to-3D, yang terus maju, dianggap sebagai tempat liputan seterusnya dalam medan AIGC selepas Difusi (imej) dan GPT (teks), dan telah mendapat perhatian yang tidak pernah berlaku sebelum ini. Tidak, produk yang dipanggil ChatAvatar telah dimasukkan ke dalam beta awam sederhana, dengan cepat memperoleh lebih 700,000 tontonan dan perhatian, dan telah dipaparkan di Spacesoftheweek. △ChatAvatar juga akan menyokong teknologi Imageto3D yang menjana aksara bergaya 3D daripada lukisan asal perspektif tunggal/berbilang perspektif Model 3D yang dihasilkan oleh versi beta semasa telah mendapat perhatian meluas.
 Yang terbaru dari Universiti Oxford! Mickey: Padanan imej 2D dalam SOTA 3D! (CVPR\'24)
Apr 23, 2024 pm 01:20 PM
Yang terbaru dari Universiti Oxford! Mickey: Padanan imej 2D dalam SOTA 3D! (CVPR\'24)
Apr 23, 2024 pm 01:20 PM
Pautan projek ditulis di hadapan: https://nianticlabs.github.io/mickey/ Memandangkan dua gambar, pose kamera di antara mereka boleh dianggarkan dengan mewujudkan kesesuaian antara gambar. Biasanya, surat-menyurat ini adalah 2D hingga 2D, dan anggaran pose kami adalah skala-tak tentu. Sesetengah aplikasi, seperti realiti tambahan segera pada bila-bila masa, di mana-mana sahaja, memerlukan anggaran pose metrik skala, jadi mereka bergantung pada penganggar kedalaman luaran untuk memulihkan skala. Makalah ini mencadangkan MicKey, proses pemadanan titik utama yang mampu meramalkan korespondensi metrik dalam ruang kamera 3D. Dengan mempelajari padanan koordinat 3D merentas imej, kami dapat membuat kesimpulan relatif metrik



