Adakah masalah persamaan N-S diselesaikan? Disandingkan dengan Hipotesis Riemann, Teka-teki Matematik Milenium sedang menanti kemenangan

Ini adalah salah satu masalah yang tidak dapat diselesaikan paling terkenal dalam matematik. Kerja baharu telah disemak bersama dan teks penuh tersedia.

Ia sedang berkembang pesat. Adakah mekanik bendalir memulakan momen superkonduktornya sendiri?

Dalam beberapa hari kebelakangan ini, orang dalam kalangan matematik sedang giat membincangkan bahawa formula Hamiltonian biasa bagi masalah Navier-Stokes akhirnya muncul - masalah yang tidak dapat diselesaikan dalam sejarah matematik ini mungkin ada jawapannya. Pada masa lalu, ini secara amnya dianggap mustahil.

Seberapa penting ini? Persamaan Navier-Stokes, seperti Hipotesis Riemann, telah disenaraikan sebagai salah satu daripada "Masalah Matematik Tujuh Milenium" pada tahun 2000.

Tujuh masalah bertaraf dunia ini ialah: Masalah NP-lengkap, tekaan Hodge, tekaan Poincaré, hipotesis Riemann, kewujudan Yang-Mills dan jurang jisim, persamaan Navier-Stokes , tekaan BSD. Setiap satu daripada tujuh masalah mempunyai ganjaran sebanyak satu juta dolar AS Dalam lebih daripada 20 tahun, hanya "Poincaré Conjecture" telah diselesaikan oleh ahli matematik Rusia yang berbakat, Perelman.

Kebanyakan mereka sudah biasa, tetapi "persamaan Navier-Stokes" (persamaan N-S) nampaknya kurang disebut di kalangan mereka. Sebabnya mungkin masalah ini terlalu sukar untuk difahami (pelajar yang telah mengikuti kursus "Mekanik Bendalir" di kolej pasti ada idea). Malah ada yang percaya bahawa ia adalah formula paling kompleks dalam sejarah matematik.

Ringkasnya, ahli matematik abad kelapan belas Euler telah memperoleh satu set persamaan dalam "Prinsip Umum Pergerakan Bendalir" berdasarkan perubahan daya dan momentum yang dialami oleh bendalir apabila bendalir inviscid bergerak.

Penerangan persamaan Euler menetapkan pergerakan bendalir dalam dunia yang ideal, tetapi terdapat geseran di dalam bendalir sebenar. Bendalir dalam alam semula jadi adalah likat dan secara kolektif dipanggil cecair likat atau cecair sebenar. Sebagai contoh, apabila kita mengacau madu, kita akan merasakan kesan kelikatan, dan rintangan pesawat terbang juga sebahagian besarnya berasal daripada kelikatan udara.

Disebabkan oleh kelikatan cecair sebenar, kajian kita tentang pergerakan bendalir menjadi sangat rumit.

Pada abad ke-19, jurutera dan ahli fizik Perancis Claude-Louis Navit dan ahli fizik dan matematik Ireland George Stokes mewujudkan keseimbangan dan gerakan bendalir dengan mempertimbangkan daya antara molekul Persamaan asas bagi , dan menerangkan bentuk komponen gerakan dalam Cartesian .

Inilah yang dipanggil oleh generasi kemudian sebagai persamaan Navier-Stokes. Salah satu persamaan pembezaan separa yang paling menakutkan sepanjang masa.

^{Persamaan Navier-Stokes digunakan untuk menerangkan bahan bendalir seperti cecair dan udara. Persamaan ini mengaitkan kadar perubahan momentum zarah bendalir (daya) kepada perubahan tekanan dan daya likat dissipative (bersamaan dengan geseran) dan graviti yang bertindak ke atas bahagian dalam bendalir. Daya likat ini timbul daripada interaksi molekul dan memberitahu kita betapa likat cecair. Dengan cara ini, persamaan Navier-Stokes menerangkan keseimbangan dinamik daya yang bertindak pada mana-mana kawasan cecair.}

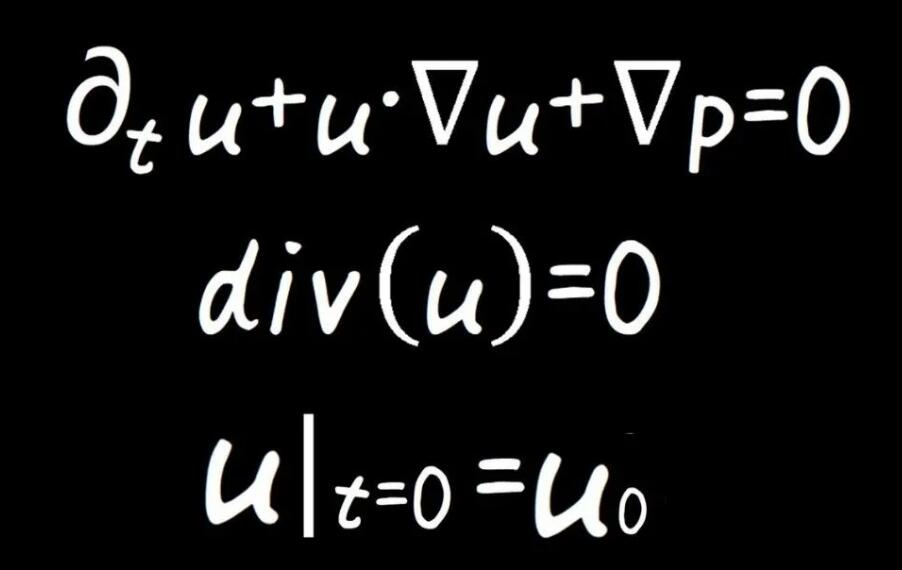
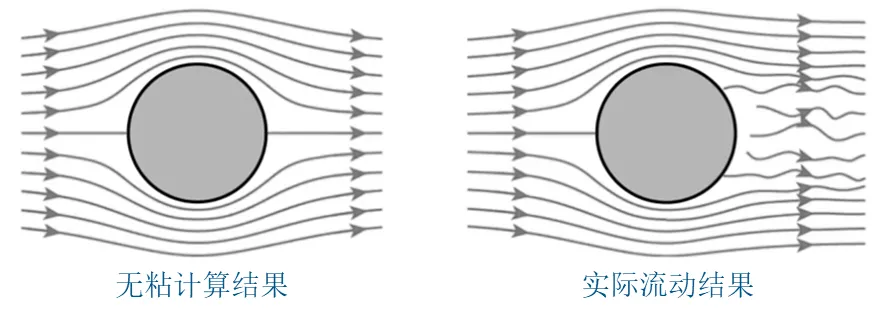
Ini penting untuk banyak masalah kejuruteraan.

Jika ada penyelesaian global untuk masalah Navier-Stokes, akan ada kejayaan dalam banyak teknologi yang berkaitan dengan mekanik bendalir, termasuk tetapi tidak terhad kepada aeroangkasa, enjin roket, ramalan cuaca, pengangkutan saluran paip dan aliran darah perubatan pembinaan modul dan sebagainya.

Perkara yang sukar tentang set persamaan ini ialah: bagaimana kita menerangkannya menggunakan teori matematik. Malah teori matematik yang menerangkan persamaan medan Einstein yang menggambarkan lubang hitam eksotik adalah lebih mudah daripada merumuskan persamaan Navier-Stokes.

Penemuan penting yang disebutkan orang-orang yang disebutkan berasal dari makalah "Formulasi Hamiltonian kanonik masalah Navier–Stokes", yang diterbitkan dalam jurnal teratas "Journal of Fluid Mechanics" dalam bidang mekanik bendalir pada 1 April:

^{Pautan kertas: https://www.cambridge.org/core/journals/journal-of-fluid-mechanics/article/canonical-hamiltonian-formulation-of-the-navierstokes-problem/B6EB960A889EB760A889EB96AEA}

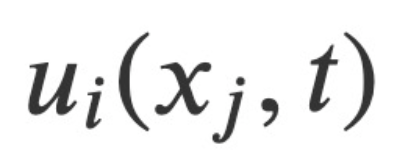Kertas kerja ini mencadangkan formula Hamiltonian baharu untuk masalah Navier-Stokes isotropik berdasarkan prinsip tindakan terkecil yang diperoleh daripada prinsip kuasa dua terkecil. Formula menggunakan halaju dan tekanan 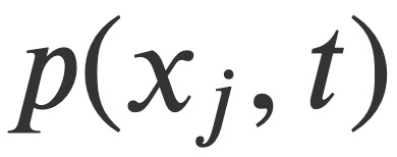sebagai kuantiti medan berubah-ubah, serta momentum konjugat kanonik yang diperoleh daripada analisis. Berdasarkan ini, kajian ini membina fungsi Hamiltonian terpelihara H* yang memenuhi persamaan kanonik Hamiltonian, dan merumuskan persamaan Hamiltonian-Jacobian yang berkaitan untuk aliran boleh mampat dan tidak boleh mampat. Persamaan Hamiltonian-Jacobian ini mengurangkan masalah mencari empat kuantiti medan bebas 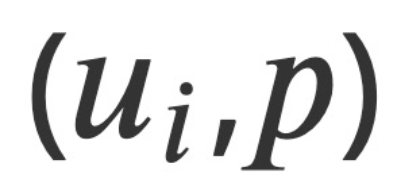kepada mencari fungsi skalar tunggal antara medan ini - fungsi utama Hamilton 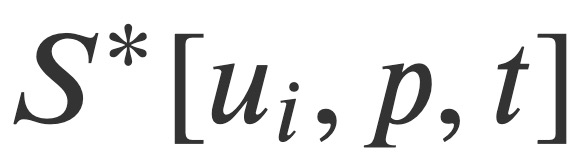Selain itu, transformasi Hamiltonian dan Jacobian Teori ini menyediakan kaedah yang ditetapkan untuk menyelesaikan masalah Navier-Stokes : cari S*.

Jika ungkapan analisis S * boleh diperolehi, maka ia akan memperoleh satu set medan baharu melalui transformasi kanonik, memberikan ungkapan analitik medan halaju dan tekanan asalnya nilai. Jika gagal, seseorang hanya boleh membuktikan bahawa penyelesaian lengkap kepada persamaan Hamilton-Jacobian wujud atau tidak wujud, yang juga akan menyelesaikan masalah kewujudan penyelesaian itu.

Adakah terdapat hadiah sejuta dolar untuk penyelidikan baharu ini? Untuk menang, penyelidik mesti menunjukkan bahawa terdapat penyelesaian kepada persamaan Navier-Stokes tidak boleh mampat tiga dimensi dan, jika terdapat penyelesaian, penyelesaian tersebut adalah lancar.

Ahli matematik Terence Tao pernah berfikir bahawa ini adalah sukar.

Berdasarkan kemajuan semasa, penyelidikan baharu telah memudahkan untuk menyelesaikan masalah terbuka, dan kami telah mengambil langkah besar ke hadapan - kami telah merealisasikan formula Hamiltonian biasa bagi persamaan Navier-Stokes, Ini mungkin bermakna kami boleh mengatasi batasan Lagrangian standard dan mengurangkan masalah untuk mencari fungsi skalar tunggal.

Mungkin kita tidak jauh untuk menyelesaikan persoalan kedua Teka-teki Milenium. Kandungan

^Reference:

^{https: //www1.grc.nasa.gov/beginners-guide-to-aeronautics/navier-strokes-equation/}

^{https: //zhuanlan.zhihu.com/p/263628141}

^{https://terrytao.wordpress.com/2007/03/18/why-global-regularity-for-navier-stokes-is-hard/}

Atas ialah kandungan terperinci Adakah masalah persamaan N-S diselesaikan? Disandingkan dengan Hipotesis Riemann, Teka-teki Matematik Milenium sedang menanti kemenangan. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!