Cara melukis angka geometri mengikut keadaan yang diketahui dalam pad lakar geometri

Sebagai contoh, diketahui bahawa dalam trapezoid ABCD, AD∥BC, AB=AD+BC, dan E ialah titik tengah CD. Buktikan: AE dan BE dibahagi dua ∠BAD dan ∠ABC masing-masing.

Kita boleh bermula dari keadaan yang diketahui dan ikuti langkah berikut untuk melukis rajah yang menepati maksud soalan pada pad lakar geometri.

Buka pad lakar geometri, gunakan [Point Tool] untuk melukis dua titik A dan B dalam ruang kosong pad lakar, pilih [Ray Tool] untuk melukis sinar mendatar melalui titik A dan B masing-masing, dan pilih titik A dan B untuk membina segmen garisan.

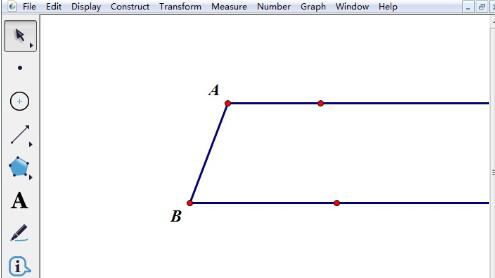
Gunakan [Point Tool] untuk memilih titik F pada segmen garis AB, ambil titik A dan B sebagai titik tengah, dan gunakan panjang AF dan BF sebagai jejari untuk melukis bulatan dua tapak bersilang pada titik D dan C. Jelas sekali, AD+BC=AB.

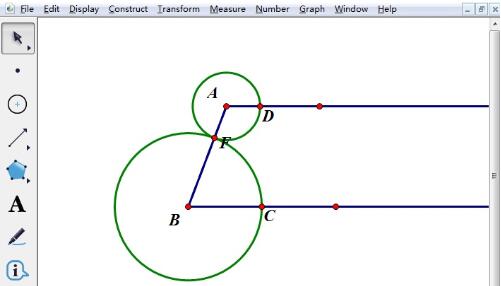
Ambil titik tengah E CD segmen garis dan sambungkan AE dan BE. Pilih titik C dan D, laksanakan arahan [Construct]-[Midpoint] untuk melukis titik tengah E, pilih titik A, E, B, dan E dalam urutan, laksanakan arahan [Construct]-[Line Segment] untuk mendapatkan garisan segmen AE, BE.

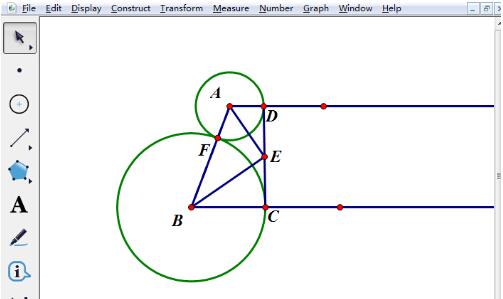
Sembunyikan grafik tambahan semasa proses lukisan untuk mendapatkan grafik yang memenuhi kehendak soalan. Pilih sinar dan bulatan yang tidak perlu dan tekan kekunci pintasan [Ctrl+H] untuk menyembunyikan objek yang tidak diperlukan dan dapatkan grafik yang menggabungkan maksud soalan seperti yang ditunjukkan dalam rajah.

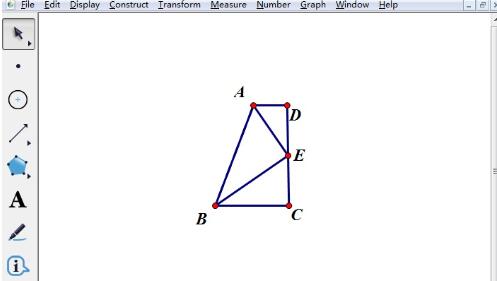
Atas ialah kandungan terperinci Cara melukis angka geometri mengikut keadaan yang diketahui dalam pad lakar geometri. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!