Pada 10 Mac 2024, pengasas bersama Ethereum Vitalik Buterin menerbitkan artikel terbaru "Bagaimana untuk bersusah payah untuk menyelamatkan kebanyakan dana pengguna" di Forum Penyelidikan Ethereum (ethresear.ch) dalam kecemasan kuantum" [1], artikel itu menyatakan: Ancaman serangan pengkomputeran kuantum yang dihadapi oleh ekosistem Ethereum boleh digunakan untuk melindungi keselamatan dana pengguna melalui strategi garpu pemulihan dan teknologi kriptografi anti-kuantum.
Apakah sebenarnya ancaman keselamatan kuantum terhadap rantaian blok?
Pengkomputeran kuantum [2] ialah model pengkomputeran baharu yang menggunakan mekanik kuantum untuk mengawal unit maklumat kuantum untuk pengiraan Ia telah dicadangkan pada tahun 1980-an selepas konsep itu dicadangkan, komputer kuantum hanya kekal dalam peringkat teori abstrak. Sehingga pertengahan 1990-an, terdapat dua algoritma kuantum: Algoritma Shor [3] (yang menyelesaikan masalah sukar penguraian nombor besar dan logaritma diskret dalam masa polinomial) dan algoritma Grover [4] (yang menyediakan carian menyeluruh untuk data tidak berstruktur). cadangan pecutan kuadratik telah membolehkan pengkomputeran kuantum melompat keluar daripada peringkat teori abstrak dan memasuki peringkat baharu penyelidikan dan pembangunan pembawa fizikal, yang kini dipanggil komputer kuantum. Rajah di bawah menunjukkan peta hala tuju pembangunan qubit fizikal komputer kuantum dari 1998 hingga 2026:
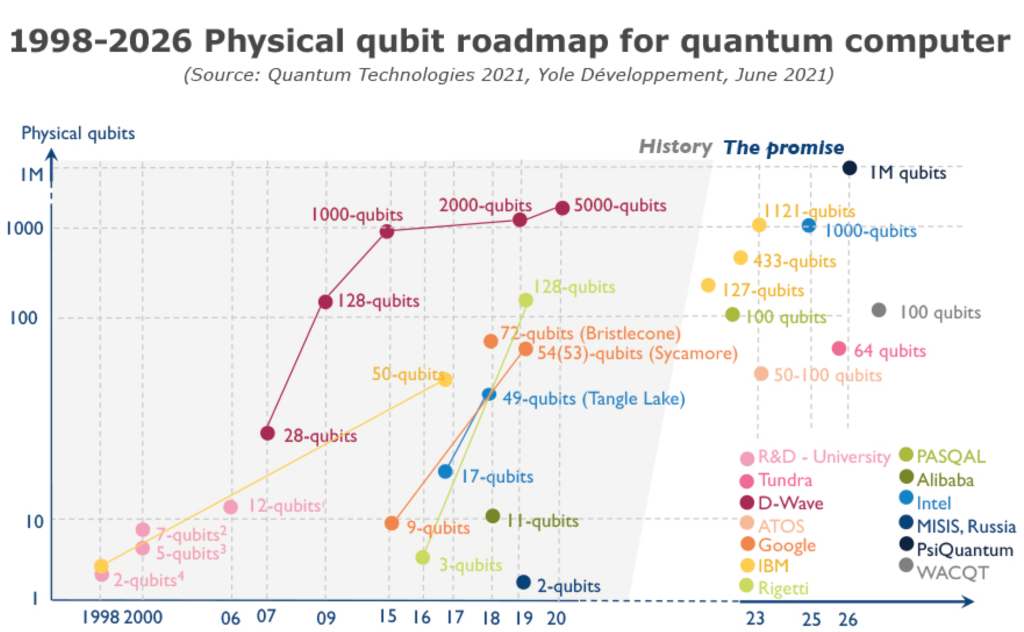
Pengkomputeran kuantum bukan ubat penawar, dan ia tidak menyelesaikan semua masalah pengkomputeran. Pada masa ini, ia boleh digunakan dalam simulasi (mensimulasikan proses yang berlaku di alam semula jadi, sesuai untuk kejuruteraan kimia dan biologi), mentafsir (memecahkan kebanyakan sistem kriptografi tradisional, sesuai untuk keselamatan rangkaian), pengoptimuman (mencari penyelesaian optimum antara pilihan yang boleh dilaksanakan, sesuai untuk kewangan, rantaian bekalan) dan masalah domain khusus lain.
Aplikasi meluas semasa blockchain datang daripada fakta bahawa ia membawa asas kepercayaan baharu kepada kerjasama antara pihak yang meminta yang berbeza, dan asas kepercayaan ini adalah berdasarkan jaminan keselamatan yang disediakan oleh kriptografi asas:
Can Trusted identity dan pengesahan pihak berkuasa urus niaga: Wujudkan identiti dipercayai pengguna berdasarkan pasangan kunci awam dan persendirian yang tidak simetri, dan urus maklumat identiti secara bersatu. Pemilikan aset digital disahkan melalui tandatangan digital, dan pemegang kunci persendirian dengan tandatangan yang sah sebenarnya memiliki aset tersebut.
Konsensus teras dan keselamatan operasi: Bina mekanisme konsensus berdasarkan teknologi kriptografi moden seperti fungsi cincang, tandatangan ambang dan fungsi rawak yang boleh disahkan untuk memastikan keselamatan mekanisme konsensus.
Perlindungan privasi dan perkongsian selamat: Bina penyelesaian perlindungan privasi berdasarkan teknologi kriptografi yang kaya dengan fungsi seperti bukti sifar pengetahuan, pengiraan berbilang pihak yang selamat dan homomorfik sepenuhnya untuk mencapai perkongsian data yang selamat pada rantaian blok.
Aplikasi penyeliaan dan pematuhan yang boleh dikawal: Mengintegrasikan dan menggunakan teknologi kriptografi seperti tandatangan cincin, skim kriptografi homomorfik, alamat tersembunyi dan perkongsian rahsia untuk memastikan penyeliaan yang selamat bagi transaksi rantaian blok.
Penggunaan kriptografi kunci awam boleh dibahagikan secara kasar kepada: mekanisme tandatangan digital yang digunakan untuk mengelakkan gangguan transaksi pada rantai, dan protokol penghantaran selamat yang digunakan untuk komunikasi antara nod. Dijejaskan oleh algoritma Shor, keselamatan kriptografi kunci awam di atas tidak dapat dijamin dengan berkesan. Semasa mempertimbangkan masa yang diperlukan untuk komputer kuantum pemecah kod khusus untuk dilaksanakan secara besar-besaran, adalah penting juga untuk mempertimbangkan berapa lama data yang disimpan pada blockchain perlu disimpan dan berapa lama masa yang diperlukan untuk sistem blockchain sedia ada untuk ditingkatkan kepada tahap keselamatan kuantum. Jika jumlah dua kali yang terakhir adalah lebih besar daripada yang pertama, maka data pada blockchain akan tertakluk kepada ancaman keselamatan yang serius yang dibawa oleh pengkomputeran kuantum.
Mengambil kira situasi semasa peningkatan kuasa pengkomputeran yang disebabkan oleh perkembangan pesat pengkomputeran kuantum, pada masa ini terdapat dua pendekatan teknikal utama yang boleh menangani risiko keselamatan dengan berkesan:
Kriptografi pasca-kuantum berdasarkan masalah matematik baharu tanpa menggunakan peralatan fizikal [ 5] Laluan teknikal;
Kriptografi kuantum berdasarkan prinsip fizikal dengan bantuan peralatan fizikal khas [6] Laluan teknikal.
Mengambil kira pelbagai faktor seperti pengesahan pelaksanaan dan faktor lain, untuk memastikan keselamatan blockchain di bawah evolusi jangka panjang, atas premis serasi dengan keselamatan kata laluan sedia ada, kami boleh mempertimbangkan untuk menggunakan blockchain terlebih dahulu melalui penghijrahan kriptografi pasca-kuantum Naik taraf kepada tahap keselamatan kuantum. Sebaik-baiknya, menaik taraf algoritma kriptografi kunci awam yang digunakan oleh blockchain sedia ada kepada algoritma kriptografi pasca-kuantum selamat kuantum harus memenuhi ciri-ciri berikut sebanyak mungkin:
Kuncinya kecil dan tandatangannya pendek: setiap pengguna di blockchain Setiap transaksi akan mengandungi maklumat tandatangan, dan kunci awam untuk mengesahkan sebarang transaksi juga disimpan pada rantaian. Jika saiz kunci dan tandatangan terlalu besar, ia akan meningkatkan kos penyimpanan dan overhed komunikasi blokchain
Kecekapan pengiraan yang tinggi: Bilangan transaksi yang boleh diproses dalam setiap tempoh masa apabila rantaian blok itu; larian sebahagian besarnya berkaitan dengan Ia berkaitan dengan masa berjalan algoritma, terutamanya algoritma pengesahan tandatangan. Kecekapan pengkomputeran algoritma yang lebih pantas boleh menyokong aplikasi blockchain berprestasi tinggi dengan lebih baik. . sistem kriptografi utama;
Bergantung kepada masalah matematik baharu;
Pada masa ini terdapat lima laluan teknologi pembinaan arus perdana, seperti ditunjukkan dalam rajah di bawah dari kiri ke kanan ia adalah kekisi, pengekodan, berbilang pembolehubah, pencincangan dan homologi:
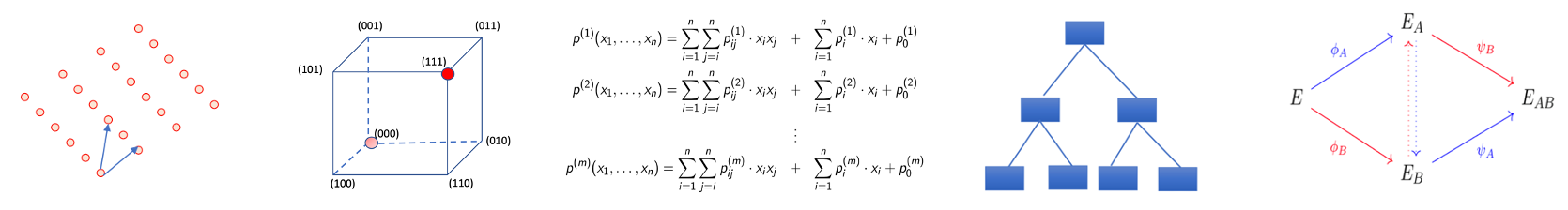
Kekisi: berdasarkan kekisi Sukar. soalan.
Pengekodan: Berdasarkan kesukaran menyahkod.
Multivariable: Berdasarkan kebolehlaksanaan kumpulan polinomial kuadratik multivariate ke atas medan terhingga.
Hash: Rintangan perlanggaran berdasarkan fungsi cincang.
Asal yang sama: berjalan pseudo rawak berdasarkan lengkung eliptik super tunggal.
Generasi baharu algoritma kriptografi secara semula jadi akan melibatkan penubuhan sistem kriptografi standard. Perkara yang paling penting tentang piawaian kriptografi pasca kuantum ialah: projek penyeragaman kriptografi pasca kuantum Institut Piawaian dan Teknologi Kebangsaan (NTST) [7], yang dilancarkan pada 2016 dan kini pada dasarnya telah memasuki penghujung perumusan penyeragaman kriptografi pasca-kuantum. Mengimbas kembali garis masa penyeragaman hampir sepuluh tahun ini, NIST secara rasmi mengumumkan empat algoritma calon standard kriptografi pasca kuantum [8] pada:
Pada 5 Julai 2022:
Penyulitan kunci awam/pengkapsulan kunci: CRYSTALS -KY;
Tandatangan digital: CRYSTALS-Dilithium, FALCON;
Antaranya, CRYSTALS-KYBER, CRYSTALS-Dilithium, dan FALCON semuanya adalah algoritma kriptografi kekisi, tetapi ketiga-tiganya adalah algoritma kriptografi yang berbeza adalah berdasarkan masalah MLWE yang sukar bagi kekisi modular, Dilithium adalah berdasarkan kepada masalah MLWE dan MSIS yang sukar bagi kekisi modular, dan FALCON berdasarkan masalah SIS yang sukar bagi kekisi NTRU sebagai tambahan, SPHINCS+ ialah tandatangan cincang tanpa kewarganegaraan algoritma.
Pada 24 Ogos 2023, CRYSTALS-KYBER, CRYSTALS-Dilithium, dan SPHINCS+ telah dibentuk menjadi draf standard FIPS203, FIPS 204 dan FIPS205 [9] juga akan diumumkan pada tahun 2024.
Tidak sukar untuk melihat bahawa kebanyakan algoritma standard yang dipilih oleh NIST pada masa ini adalah berdasarkan laluan teknikal kriptografi kekisi. Tetapi NIST tidak meletakkan telur dalam bakul yang sama Mereka juga sedang giat mencari pelbagai pilihan selain daripada pembinaan kekisi: semasa mengumumkan empat algoritma standard pada tahun 2022, mereka juga mengumumkan pelancaran pusingan keempat algoritma standard kriptografi pasca-kuantum. kerja, pusingan ini memfokuskan pada penyulitan kunci awam/algoritma pengkapsulan kunci, dan algoritma yang dipilih tidak berdasarkan struktur kekisi. Di samping itu, pusingan baharu untuk algoritma tandatangan digital juga telah dilancarkan secara bebas daripada pusingan keempat penilaian Ia bertujuan untuk memperkayakan portfolio algoritma tandatangan pasca-kuantum, jadi ia lebih memfokuskan pada struktur algoritma berasaskan kekisi yang berbeza dalam struktur algoritma Satu cadangan baharu dengan saiz tandatangan algoritma yang kecil dan kelajuan pengesahan yang pantas.
Sebagai tambahan kepada standard NIST, International Internet Standardization Organization IETF menyeragamkan algoritma tandatangan hash stateful XMSS sebagai RFC 8391[10] dan LMS sebagai RFC 8554[11] masing-masing pada 2018 dan 2019, dan ia telah diterima oleh NIST.
Pada 10 April 2024, artikel cikgu Chen Yilei "Algoritma Kuantum untuk Masalah Kekisi" [12] mengenai eprint menimbulkan sensasi dalam dunia akademik. Kertas ini memberikan algoritma kuantum masa polinomial untuk menyelesaikan masalah sukar pada kekisi Algoritma ini mempunyai kesan yang besar pada banyak skema kriptografi berdasarkan masalah sukar pada kekisi, dan boleh menyebabkan banyak algoritma tidak lagi mempunyai keupayaan untuk menahan serangan komputer kuantum. Sebagai contoh, Algoritma penyulitan homomorfik yang digunakan secara meluas pada masa ini berdasarkan andaian LWE. Ketepatan algoritma dalam kertas itu belum diketahui.
Kesukaran masalah LWE telah diberikan demonstrasi yang ketat oleh Oded Regev dalam kertas "Pada kekisi, pembelajaran dengan ralat, kod linear rawak, dan kriptografi" [13]. Kesukaran dikurangkan kepada masalah pensampelan Gaussian diskret pada kekisi, dan masalah pensampelan Gaussian diskret boleh dengan mudah dikurangkan kepada masalah klasik seperti GapSVP, SIVP (sudah tentu, setiap masalah khusus mempunyai parameter tertentu, yang diabaikan di sini). Tunjukkan bahawa masalah LWE lebih sukar daripada masalah kekisi klasik ini. Selepas kesukaran masalah LWE telah dikurangkan dengan ketat, kerana strukturnya yang mudah, sejumlah besar skim kriptografi berdasarkan LWE telah diikuti, meliputi primitif kriptografi asas seperti penyulitan (homomorfik), tandatangan, dan pertukaran kunci serta primitif kriptografi lanjutan seperti penyulitan berasaskan identiti dan penyulitan atribut. Antaranya, yang digunakan secara meluas dalam industri terutamanya penyulitan homomorfik sepenuhnya dan algoritma standard pasca-kuantum (KYBER, Dilithium, dll.) yang diumumkan oleh NIST yang disebutkan di atas.


Selepas kertas itu didedahkan kepada umum, ia menimbulkan kegemparan hebat dalam komuniti akademik dan mencetuskan perbincangan di kalangan ramai profesional. Walau bagaimanapun, disebabkan kesukaran yang melampau untuk memahami kertas itu, mungkin terdapat kurang daripada 5 sarjana di dunia yang dapat memahami sepenuhnya kandungan kertas itu, dan mungkin mengambil masa 1-2 tahun untuk mengesahkan sepenuhnya ketepatan kertas itu. Pada masa ini, ramai orang telah menyatakan beberapa pendapat yang berkaitan pada beberapa forum, akaun awam, Zhihu dan platform lain Semua orang sedang menganalisis kesan jika algoritma dalam kertas itu betul belum lagi Seseorang boleh membuat kesimpulan. Antaranya, pakar kriptografi terkenal N. P. Smart menerbitkan artikel blog "Implikasi Cadangan Serangan Kuantum terhadap LWE" [14], yang memperincikan kesan serangan ini dan beberapa pendapat ia diringkaskan seperti berikut:
Kertas ini mempunyai. belum diluluskan. Semakan rakan sebaya, walaupun ia terbukti betul, bergantung pada komputer kuantum, jadi selagi komputer kuantum belum tersedia, ia tidak akan memberi kesan kepada skim kriptografi yang sedang digunakan.
Menurut keputusan yang diberikan dalam kertas: masih mustahil untuk memecahkan algoritma piawai Kyber dan Dilithium yang sebelum ini diberikan oleh NIST, tetapi NIST mungkin menilai semula parameter algoritma ini.
Untuk algoritma penyulitan homomorfik RLWE yang biasa digunakan, seperti BFV/CKKS/BGV, algoritma ini berada dalam keupayaan serangan kertas ini. Walau bagaimanapun, sama ada dari perspektif akademik atau industri, "homomorfisme" teknologi penyulitan homomorfik adalah lebih menarik daripada "rintangan kuantum", dan hanya sedikit orang yang akan menggunakan RLWE untuk mengejar "rintangan kuantum". algoritma penyulitan, seperti skema kriptografi berdasarkan lengkung eliptik, bergantung pada masalah keras logaritma diskret, dan algoritma kuantum untuk menyelesaikan masalah ini telah dicadangkan sangat awal, tetapi ahli akademik dan industri masih mengkaji dan menggunakan skema ini.
Berita terkini: Terdapat masalah dengan pengiraan tesis Teacher Chen, dan penggera kata laluan grid telah ditarik balik buat sementara waktu.

[1] https://ethresear.ch/t/how-to-hard-fork-to-save-most-users-funds-in-a-quantum-emergency/18901/ 9
[2] Benioff P. Komputer sebagai sistem fizikal: Model komputer Hamiltonian mekanik kuantum mikroskopik seperti yang diwakili oleh mesin Turing[J]. 3] Shor P W. Algoritma untuk pengiraan kuantum: logaritma diskret dan pemfaktoran[C]//Prosiding Simposium tahunan ke-35 mengenai asas sains komputer Ieee, 1994: 124-134.
[4] Grover L K. A fast quantum. algoritma mekanikal untuk carian pangkalan data[C]//Prosiding simposium ACM tahunan kedua puluh lapan 1996: 212-219.
[5] Bernstein, D.J (2009). : Bernstein, D.J., Buchmann, J., Dahmen, E. (eds) Post-Quantum Cryptography, Berlin, Heidelberg.
[6] Gisin N, Ribordy G, Tittel W, et al. . Ulasan fizik moden, 2002, 74(1): 145.
[7]
https://csrc.nist.gov/Projects/post-quantum-cryptography/post-quantum-cryptography-standardization[ 8]
https://csrc.nist.gov/News/2022/pqc-candidates-to-be-standardized-and-round-4[9]
https://csrc.nist.gov/News /2023/three-draft-fips-for-post-quantum-cryptography[10] Huelsing, A., Butin, D., Gazdag, S., Rijneveld, J., dan A. Mohaisen, "XMSS: Skim Tandatangan Merkle eXtended", RFC 8391, DOI 10.17487/RFC8391, Mei 2018, https://www.rfc-editor.org/info/rfc8391
>.[11] McGrew, McGrew, D. , M., dan S. Fluhrer, "Tandatangan Berasaskan Hash Leighton-Micali", RFC 8554, DOI 10.17487/RFC8554, April 2019, https://www.rfc-editor.org/info/rfc8554
> ;.[12] Chen Y. Algoritma Kuantum untuk Masalah Kekisi[J]. Arkib ePrint Kriptologi, 2024.
[13] Regev O. Pada kekisi, pembelajaran dengan ralat, kod linear rawak dan kriptografi[J]. Journal of the ACM (JACM), 2009, 56(6): 1-40.
[14]
https://nigelsmart.github.io/LWE.htmlArtikel ini ditulis oleh ZAN Team ( Akaun X @ Ditulis bersama oleh Dongni dan Jiaxing dari zan_team).
Atas ialah kandungan terperinci Kuantum Kesenangan untuk Kriptozoologi Lattice? Satu artikel akan membantu anda menganalisis kontroversi akademik kriptografi kekisi. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!




