Perbincangan ringkas mengenai pelaksanaan lapan pengisihan utama dalam kemahiran javascript

Sebulan memasuki tahun persekolahan, saya telah mengimpikan soalan algoritma struktur data muncul dalam peperiksaan bertulis berkali-kali Saya lebih takut kepada struktur data daripada mana-mana "hantu". Haha, nampaknya sangat perlu untuk mengkaji semula struktur data yang biasa digunakan untuk mengelakkan "mimpi ngeri" daripada menjadi kenyataan.

Tidak perlu diperkatakan kepentingan asas pengaturcaraan seperti struktur data, mari kita terus ke intinya.

Algoritma pengisihan dibahagikan kepada pengisihan dalaman dan pengisihan luaran. Pengisihan dalaman menggunakan memori, dan hanya pengisihan dalaman dibincangkan di sini.

1. Isih sisipan: isihan sisipan langsung dan isihan Bukit

2. Isih pilihan: isihan pilihan mudah dan isihan timbunan

3. Isih pertukaran: isihan gelembung dan isihan pantas

4, cantumkan isihan

5, jenis radix

Isihan sisipan langsung

Idea asas: Dalam set nombor yang hendak diisih, dengan mengandaikan bahawa nombor sebelumnya (n-1) [n>=2] sudah tersusun, mula-mula masukkan nombor ke-n ke dalam nombor tertib sebelumnya, Jadi bahawa n nombor ini juga disusun. Ulangi kitaran ini sehingga semuanya teratur.

Isih bukit

Idea asas: Algoritma membahagikan set nombor terlebih dahulu untuk diisih kepada beberapa kumpulan mengikut kenaikan tertentu d (n/2, n ialah nombor yang hendak diisih), dan subskrip yang direkodkan dalam setiap kumpulan berbeza dengan d . Lakukan isihan sisipan terus pada semua elemen dalam setiap kumpulan, kemudian kumpulkan mereka dengan kenaikan yang lebih kecil (d/2), dan lakukan isihan sisipan terus pada setiap kumpulan. Apabila kenaikan dikurangkan kepada 1, pengisihan selesai selepas pengisihan sisipan terus.

Isih pilihan mudah

Idea asas: Daripada set nombor yang hendak diisih, pilih nombor terkecil dan tukarkannya dengan nombor di kedudukan pertama, kemudian cari nombor terkecil di antara nombor yang tinggal dan tukarkannya dengan nombor di kedudukan kedua , jadi Cari haha hingga nombor kedua hingga nombor terakhir dan nombor terakhir.

Isih timbunan

Idea asas: Isihan timbunan ialah jenis pemilihan pokok, yang merupakan penambahbaikan yang berkesan pada isihan pemilihan langsung.

Jujukan (h1, h2,...,hn) dengan n elemen, jika dan hanya jika (hi>=h2i,hi>=2i 1) atau (hi<=h2i,hi<=2i 1 ) ( i=1,2,...,n/2) dipanggil timbunan. Hanya timbunan yang memenuhi syarat dahulu dibincangkan di sini. Ia boleh dilihat daripada definisi timbunan bahawa elemen atas timbunan (iaitu, elemen pertama) mestilah item terbesar (timbunan atas besar). Pokok binari yang lengkap boleh mewakili struktur timbunan dengan sangat intuitif. Bahagian atas timbunan ialah akar, dan yang lain adalah subpokok kiri dan subpokok kanan. Pada mulanya, urutan nombor yang hendak diisih dianggap sebagai pokok binari yang disimpan secara berurutan, dan susunan penyimpanannya dilaraskan supaya ia menjadi timbunan Pada masa ini, bilangan nod akar timbunan adalah yang terbesar. Kemudian tukar nod akar dengan nod terakhir timbunan. Kemudian laraskan semula nombor sebelumnya (n-1) untuk membentuk timbunan. Dan seterusnya, sehingga terdapat timbunan dengan hanya dua nod, dan mereka ditukar, dan akhirnya urutan tertib n nod diperoleh. Daripada huraian algoritma, pengisihan timbunan memerlukan dua proses, satu adalah untuk menubuhkan timbunan, dan satu lagi adalah untuk menukar kedudukan antara bahagian atas timbunan dan elemen terakhir timbunan. Jadi jenis timbunan terdiri daripada dua fungsi. Satu ialah fungsi penembusan untuk membina timbunan, dan satu lagi ialah fungsi untuk memanggil berulang kali fungsi penembusan untuk melaksanakan pengisihan.

Isih gelembung

Idea asas: Dalam satu set nombor yang hendak diisih, bandingkan dan laraskan dua nombor bersebelahan dalam urutan dari atas ke bawah untuk semua nombor dalam julat yang belum diisih, supaya lebih besar Sedikit tenggelam, dan yang lebih kecil naik. Iaitu: apabila dua nombor bersebelahan dibandingkan dan didapati pesanan mereka bertentangan dengan keperluan pesanan, ia ditukar.

Isih Pantas

Idea asas: Pilih elemen penanda aras, biasanya elemen pertama atau elemen terakhir, dan bahagikan urutan untuk diisih kepada dua bahagian melalui satu imbasan, satu bahagian lebih kecil daripada elemen penanda aras dan bahagian lain lebih besar daripada atau sama dengan elemen penanda aras Pada masa ini, penanda aras Elemen berada dalam kedudukan diisih yang betul, dan kemudian kedua-dua bahagian yang dibahagikan diisih secara rekursif dengan cara yang sama.

Gabung isihan

Pengisihan asas: Kaedah pengisihan gabungan adalah untuk menggabungkan dua (atau lebih) senarai tertib ke dalam senarai tertib baharu, iaitu urutan yang hendak diisih dibahagikan kepada beberapa urutan, setiap urutan mempunyai urutan. Kemudian gabungkan urutan tertib ke dalam urutan tertib keseluruhan.

Isih radix

Idea asas: Satukan semua nilai untuk dibandingkan (integer positif) dengan panjang digit yang sama dan tambah sifar di hadapan nombor dengan digit yang lebih pendek. Kemudian, bermula dari bit terendah, susun satu persatu. Dengan cara ini, selepas mengisih daripada bit terendah ke bit tertinggi, jujukan menjadi jujukan tertib.

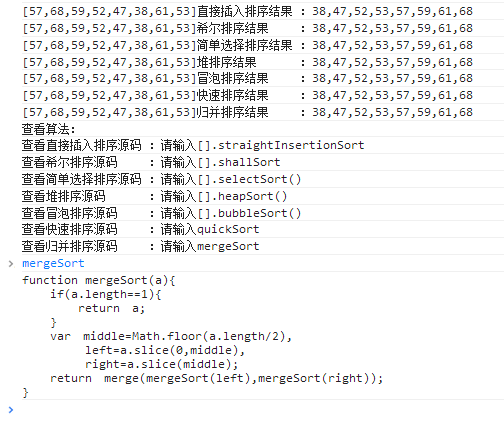
Alamat tunjuk cara kod: http://lovermap.sinaapp.com/test/sort.html

Kini kami menganalisis kestabilan 8 algoritma pengisihan.

(Netizen diminta memahami kestabilan pengisihan dengan menggabungkan idea asas pengisihan sebelum ini (idea asas 8 jenis pengisihan telah disebut sebelum ini dan tidak akan diulang di sini) jika tidak mungkin agak kabur)

(1) Isih sisipan langsung : Secara umum isihan sisipan, perbandingan bermula dari elemen terakhir urutan tertib Jika ia lebih besar daripadanya, ia dimasukkan terus di belakangnya, jika tidak, ia akan kekal membandingkan ke hadapan. Jika elemen yang sama dengan elemen yang dimasukkan ditemui, ia dimasukkan selepas elemen yang sama. Isihan sisipan adalah stabil.

(2) Isih bukit : Isih bukit ialah isihan sisipan unsur mengikut panjang penyegerakan yang berbeza Isihan sisipan adalah stabil dan tidak akan mengubah susunan relatif unsur yang sama, tetapi dalam Semasa yang berbeza proses isihan sisipan, unsur yang sama mungkin bergerak dalam jenis sisipan masing-masing, dan kestabilan akan musnah, jadi isihan Bukit tidak stabil.

(3) Pengisihan pemilihan mudah : Dalam satu pilihan, jika elemen semasa lebih kecil daripada elemen, dan elemen kecil muncul di belakang elemen yang sama dengan elemen semasa, maka ia akan stabil selepas pertukaran Seks musnah. Ia mungkin agak kabur hanya untuk mengatakannya, mari lihat contoh kecil: 858410, dalam imbasan pertama, elemen pertama 8 akan ditukar dengan 4, maka susunan relatif kedua-dua 8 dalam urutan asal adalah tidak konsisten dengan jujukan asal, jadi pengisihan pemilihan tidak mungkin Stablize.

(4) Isihan timbunan : Proses pengisihan timbunan adalah untuk memilih yang terbesar (timbunan atas besar) atau yang terkecil (timbunan atas kecil) bermula dari n/2 dan nod anaknya dengan jumlah 3 nilai Ini Pilihan antara 3 elemen pastinya tidak memusnahkan kestabilan. Tetapi apabila memilih elemen untuk nod induk n/2-1, n/2-2, ..., ada kemungkinan nod induk n/2 menukar elemen seterusnya, dan n/2-1 Nod induk tidak tukar elemen yang sama pada penghujungnya, jadi pengisihan timbunan tidak stabil.

(5) Isih gelembung : Seperti yang dapat dilihat daripada kandungan sebelumnya, isihan gelembung ialah perbandingan dua elemen bersebelahan, dan pertukaran juga berlaku antara kedua-dua elemen ini jika kedua-dua elemen adalah sama , tak perlu tukar. Jadi jenis gelembung adalah stabil.

(6) Isih pantas : Apabila elemen pusat ditukar dengan elemen dalam jujukan, ia berkemungkinan besar akan mengganggu kestabilan elemen sebelumnya. Mari lihat contoh kecil: 6 4 4 5 4 7 8 9. Dalam pas pengisihan pertama, pertukaran elemen pusat 6 dan 4 ketiga akan memusnahkan jujukan asal unsur 4, jadi isihan pantas tidak stabil.

(7) Isih Gabung : Dalam sub-lajur yang terurai, apabila terdapat 1 atau 2 elemen, 1 elemen tidak akan ditukar, dan 2 elemen tidak akan ditukar jika saiznya sama. . Semasa proses penggabungan jujukan, jika kedua-dua elemen semasa adalah sama, kami menyimpan unsur-unsur jujukan sebelumnya di hadapan jujukan hasil, jadi isihan gabungan juga stabil.

(8) Isih Radix : Isih mengikut tertib rendah dahulu, dan kemudian kumpulkan mengikut urutan tinggi, dan kemudian kumpulkan, sehingga tertib tertinggi. Kadangkala beberapa atribut mempunyai susunan keutamaan Ia diisih mengikut keutamaan rendah dahulu, dan kemudian mengikut keutamaan tinggi Urutan terakhir ialah mereka yang mempunyai keutamaan tinggi didahulukan, dan yang mempunyai keutamaan tinggi dan keutamaan yang sama didahulukan. Isihan Radix adalah berdasarkan isihan berasingan dan koleksi berasingan, jadi ia stabil.

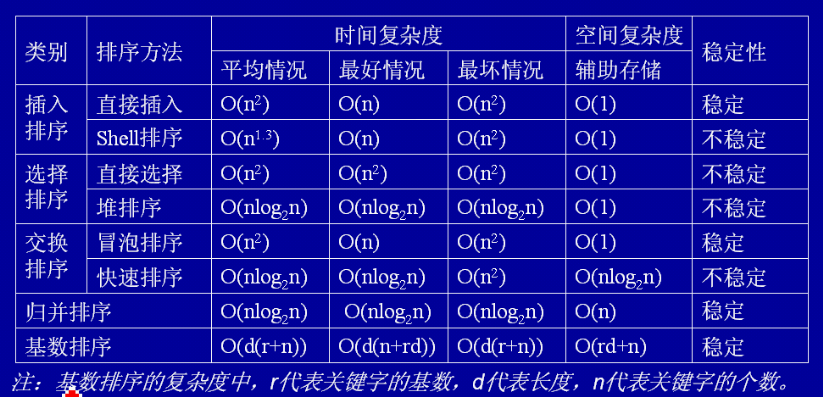
Ringkasan klasifikasi, kestabilan, kerumitan masa dan kerumitan ruang 8 jenis pengisihan: