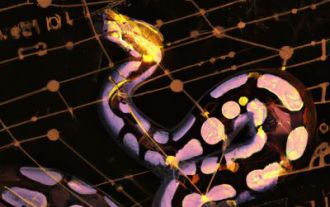
如何用简单的算法生成一个类似『光盘』的彩色圆形图片？
大概就像下图所示的样子
回复内容：
补充一下MATLAB的代码：<span class="n">t</span> <span class="p">=</span> <span class="p">(</span><span class="mi">0</span><span class="p">:.</span><span class="mi">02</span><span class="p">:</span><span class="mi">2</span><span class="p">)</span><span class="o">*</span><span class="nb">pi</span><span class="p">;</span> <span class="n">r</span> <span class="p">=</span> <span class="mi">0</span><span class="p">:.</span><span class="mi">02</span><span class="p">:</span><span class="mi">1</span><span class="p">;</span> <span class="n">pcolor</span><span class="p">(</span><span class="nb">cos</span><span class="p">(</span><span class="n">t</span><span class="p">)</span><span class="o">'*</span><span class="n">r</span><span class="p">,</span><span class="nb">sin</span><span class="p">(</span><span class="n">t</span><span class="p">)</span><span class="o">'*</span><span class="n">r</span><span class="p">,</span><span class="n">t</span><span class="o">'*</span><span class="p">(</span><span class="n">r</span><span class="o">==</span><span class="n">r</span><span class="p">))</span> <span class="n">colormap</span><span class="p">(</span><span class="n">hsv</span><span class="p">(</span><span class="mi">256</span><span class="p">)),</span> <span class="n">shading</span> <span class="n">interp</span><span class="p">,</span> <span class="n">axis</span> <span class="n">image</span> <span class="n">off</span>
基本上就是在这个圆上颜色的色相(Hue)，只与该点与圆心连线的夹角有关。知道这一点你就做一幅图像，然后遍历每一个点，把该点的坐标值
转换为极坐标，色相值就是极坐标角度。用 matplotlib 实现的话有个小技巧，把imshow的cmap改为hsv就可以直接按照色相来画。
<span class="c"># -*- coding:utf-8 -*-</span>
<span class="kn">from</span> <span class="nn">pylab</span> <span class="kn">import</span> <span class="o">*</span>
<span class="n">center</span> <span class="o">=</span> <span class="p">(</span><span class="mi">250</span><span class="p">,</span> <span class="mi">250</span><span class="p">)</span>
<span class="n">radius</span> <span class="o">=</span> <span class="mi">250</span>
<span class="n">img</span> <span class="o">=</span> <span class="n">zeros</span><span class="p">((</span><span class="mi">500</span><span class="p">,</span><span class="mi">500</span><span class="p">))</span>
<span class="k">for</span> <span class="n">i</span> <span class="ow">in</span> <span class="nb">range</span><span class="p">(</span><span class="mi">500</span><span class="p">):</span>
<span class="k">for</span> <span class="n">j</span> <span class="ow">in</span> <span class="nb">range</span><span class="p">(</span><span class="mi">500</span><span class="p">):</span>
<span class="n">x</span> <span class="o">=</span> <span class="n">i</span> <span class="o">-</span> <span class="n">center</span><span class="p">[</span><span class="mi">0</span><span class="p">]</span> <span class="o">*</span> <span class="mf">1.0</span>
<span class="n">y</span> <span class="o">=</span> <span class="n">j</span> <span class="o">-</span> <span class="n">center</span><span class="p">[</span><span class="mi">1</span><span class="p">]</span> <span class="o">*</span> <span class="mf">1.0</span>
<span class="k">if</span> <span class="n">x</span><span class="o">**</span><span class="mi">2</span><span class="o">+</span><span class="n">y</span><span class="o">**</span><span class="mi">2</span> <span class="o"><</span> <span class="n">radius</span><span class="o">**</span><span class="mi">2</span><span class="p">:</span>
<span class="k">if</span> <span class="n">x</span> <span class="o">></span> <span class="mi">0</span><span class="p">:</span>
<span class="n">img</span><span class="p">[</span><span class="n">i</span><span class="p">,</span><span class="n">j</span><span class="p">]</span> <span class="o">=</span> <span class="n">arctan</span><span class="p">(</span><span class="n">y</span><span class="o">/</span><span class="n">x</span><span class="p">)</span>
<span class="k">elif</span> <span class="n">x</span><span class="o"><</span><span class="mi">0</span> <span class="ow">and</span> <span class="n">y</span><span class="o">>=</span><span class="mi">0</span><span class="p">:</span>
<span class="n">img</span><span class="p">[</span><span class="n">i</span><span class="p">,</span><span class="n">j</span><span class="p">]</span> <span class="o">=</span> <span class="n">arctan</span><span class="p">(</span><span class="n">y</span><span class="o">/</span><span class="n">x</span><span class="p">)</span> <span class="o">+</span> <span class="n">pi</span>
<span class="k">elif</span> <span class="n">x</span><span class="o"><</span><span class="mi">0</span> <span class="ow">and</span> <span class="n">y</span><span class="o"><</span><span class="mi">0</span><span class="p">:</span>
<span class="n">img</span><span class="p">[</span><span class="n">i</span><span class="p">,</span><span class="n">j</span><span class="p">]</span> <span class="o">=</span> <span class="n">arctan</span><span class="p">(</span><span class="n">y</span><span class="o">/</span><span class="n">x</span><span class="p">)</span> <span class="o">-</span> <span class="n">pi</span>
<span class="k">elif</span> <span class="n">x</span><span class="o">==</span><span class="mi">0</span> <span class="ow">and</span> <span class="n">y</span><span class="o">></span><span class="mi">0</span><span class="p">:</span>
<span class="n">img</span><span class="p">[</span><span class="n">i</span><span class="p">,</span><span class="n">j</span><span class="p">]</span> <span class="o">=</span> <span class="n">pi</span> <span class="o">/</span> <span class="mi">2</span>
<span class="k">elif</span> <span class="n">x</span><span class="o">==</span><span class="mi">0</span> <span class="ow">and</span> <span class="n">y</span><span class="o"><</span><span class="mi">0</span><span class="p">:</span>
<span class="n">img</span><span class="p">[</span><span class="n">i</span><span class="p">,</span><span class="n">j</span><span class="p">]</span> <span class="o">=</span> <span class="n">pi</span> <span class="o">/</span> <span class="o">-</span><span class="mi">2</span>
<span class="k">elif</span> <span class="n">x</span><span class="o">==</span><span class="mi">0</span> <span class="ow">and</span> <span class="n">y</span><span class="o">==</span><span class="mi">0</span><span class="p">:</span>
<span class="n">img</span><span class="p">[</span><span class="n">i</span><span class="p">,</span><span class="n">j</span><span class="p">]</span> <span class="o">=</span> <span class="mf">0.0</span>
<span class="k">print</span> <span class="n">img</span>
<span class="n">imshow</span><span class="p">(</span><span class="n">img</span><span class="p">,</span> <span class="n">cmap</span><span class="o">=</span><span class="n">cm</span><span class="o">.</span><span class="n">hsv</span><span class="p">)</span>
<span class="n">show</span><span class="p">()</span>
<span class="kn">from</span> <span class="nn">pylab</span> <span class="kn">import</span> <span class="o">*</span> <span class="n">n</span><span class="o">=</span><span class="mi">300</span> <span class="n">img</span><span class="o">=</span><span class="p">[[</span><span class="n">arctan2</span><span class="p">(</span><span class="n">x</span><span class="p">,</span><span class="n">y</span><span class="p">)</span> <span class="k">if</span> <span class="n">x</span><span class="o">*</span><span class="n">x</span><span class="o">+</span><span class="n">y</span><span class="o">*</span><span class="n">y</span><span class="o"><</span><span class="n">n</span><span class="o">*</span><span class="n">n</span> <span class="k">else</span> <span class="mi">0</span> <span class="k">for</span> <span class="n">y</span> <span class="ow">in</span> <span class="nb">range</span><span class="p">(</span><span class="o">-</span><span class="n">n</span><span class="p">,</span><span class="n">n</span><span class="p">)]</span> <span class="k">for</span> <span class="n">x</span> <span class="ow">in</span> <span class="nb">range</span><span class="p">(</span><span class="o">-</span><span class="n">n</span><span class="p">,</span><span class="n">n</span><span class="p">)]</span> <span class="n">imshow</span><span class="p">(</span><span class="n">img</span><span class="p">,</span> <span class="n">cmap</span><span class="o">=</span><span class="n">cm</span><span class="o">.</span><span class="n">hsv</span><span class="p">)</span> <span class="n">show</span><span class="p">()</span>
关于色相是什么（反正这里说的不是可以用来牺牲的那个色相了），可以参看Wiki：HSL和HSV色彩空间，那个H就是色相Hue。
有点像下面这幅图的横截面（摘自Wiki）
只不过明度Chroma没有变化。这样的话，蛮简单的啊。对每个像素算出它所在半径的角度 0~2π 然后映射到Hue的值域上就是了。
具体实现的话，话说可以用OpenCV吗？反正一些图像库里面是有HSR到RGB的转换函数的。
（我一直都不明白所谓邀请是怎么回事，以及为什么大家都爱说谢邀） 补充一下Mathematica代码
n=300;
c=Hue[i/n];
Graphics@Table[{c,EdgeForm@c,Disk[{0,0},1,2Pi/n{i-1,i}]},{i,n}]
Alat AI Hot
Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik
AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.
Undress AI Tool
Gambar buka pakaian secara percuma
Clothoff.io
Penyingkiran pakaian AI
AI Hentai Generator
Menjana ai hentai secara percuma.
Artikel Panas
Alat panas
Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma
SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan
Hantar Studio 13.0.1
Persekitaran pembangunan bersepadu PHP yang berkuasa
Dreamweaver CS6
Alat pembangunan web visual
SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)
Topik panas
Cara Menggunakan Python untuk Mencari Pengagihan Zipf Fail Teks
Mar 05, 2025 am 09:58 AM
Tutorial ini menunjukkan cara menggunakan Python untuk memproses konsep statistik undang -undang ZIPF dan menunjukkan kecekapan membaca dan menyusun fail teks besar Python semasa memproses undang -undang. Anda mungkin tertanya -tanya apa maksud pengedaran ZIPF istilah. Untuk memahami istilah ini, kita perlu menentukan undang -undang Zipf. Jangan risau, saya akan cuba memudahkan arahan. Undang -undang Zipf Undang -undang Zipf hanya bermaksud: Dalam korpus bahasa semulajadi yang besar, kata -kata yang paling kerap berlaku muncul kira -kira dua kali lebih kerap sebagai kata -kata kerap kedua, tiga kali sebagai kata -kata kerap ketiga, empat kali sebagai kata -kata kerap keempat, dan sebagainya. Mari kita lihat contoh. Jika anda melihat corpus coklat dalam bahasa Inggeris Amerika, anda akan melihat bahawa perkataan yang paling kerap adalah "th
Cara memuat turun fail di python
Mar 01, 2025 am 10:03 AM
Python menyediakan pelbagai cara untuk memuat turun fail dari Internet, yang boleh dimuat turun melalui HTTP menggunakan pakej Urllib atau Perpustakaan Permintaan. Tutorial ini akan menerangkan cara menggunakan perpustakaan ini untuk memuat turun fail dari URL dari Python. Permintaan Perpustakaan Permintaan adalah salah satu perpustakaan yang paling popular di Python. Ia membolehkan menghantar permintaan HTTP/1.1 tanpa menambahkan rentetan pertanyaan secara manual ke URL atau pengekodan data pos. Perpustakaan Permintaan boleh melaksanakan banyak fungsi, termasuk: Tambah data borang Tambah fail berbilang bahagian Akses data tindak balas python Buat permintaan kepala
Bagaimana saya menggunakan sup yang indah untuk menghuraikan html?
Mar 10, 2025 pm 06:54 PM
Artikel ini menerangkan cara menggunakan sup yang indah, perpustakaan python, untuk menghuraikan html. Ia memperincikan kaedah biasa seperti mencari (), find_all (), pilih (), dan get_text () untuk pengekstrakan data, pengendalian struktur dan kesilapan HTML yang pelbagai, dan alternatif (sel
Penapisan gambar di python
Mar 03, 2025 am 09:44 AM
Berurusan dengan imej yang bising adalah masalah biasa, terutamanya dengan telefon bimbit atau foto kamera resolusi rendah. Tutorial ini meneroka teknik penapisan imej di Python menggunakan OpenCV untuk menangani isu ini. Penapisan Imej: Alat yang berkuasa Penapis Imej
Cara Bekerja Dengan Dokumen PDF Menggunakan Python
Mar 02, 2025 am 09:54 AM
Fail PDF adalah popular untuk keserasian silang platform mereka, dengan kandungan dan susun atur yang konsisten merentasi sistem operasi, peranti membaca dan perisian. Walau bagaimanapun, tidak seperti Python memproses fail teks biasa, fail PDF adalah fail binari dengan struktur yang lebih kompleks dan mengandungi unsur -unsur seperti fon, warna, dan imej. Mujurlah, tidak sukar untuk memproses fail PDF dengan modul luaran Python. Artikel ini akan menggunakan modul PYPDF2 untuk menunjukkan cara membuka fail PDF, mencetak halaman, dan mengekstrak teks. Untuk penciptaan dan penyuntingan fail PDF, sila rujuk tutorial lain dari saya. Penyediaan Inti terletak pada menggunakan modul luaran PYPDF2. Pertama, pasangkannya menggunakan PIP: Pip adalah p
Cara Cache Menggunakan Redis dalam Aplikasi Django
Mar 02, 2025 am 10:10 AM
Tutorial ini menunjukkan cara memanfaatkan caching redis untuk meningkatkan prestasi aplikasi python, khususnya dalam rangka kerja Django. Kami akan merangkumi pemasangan Redis, konfigurasi Django, dan perbandingan prestasi untuk menyerlahkan bene
Memperkenalkan Toolkit Bahasa Alam (NLTK)
Mar 01, 2025 am 10:05 AM
Pemprosesan bahasa semulajadi (NLP) adalah pemprosesan bahasa manusia secara automatik atau separa automatik. NLP berkait rapat dengan linguistik dan mempunyai hubungan dengan penyelidikan dalam sains kognitif, psikologi, fisiologi, dan matematik. Dalam sains komputer
Bagaimana untuk melakukan pembelajaran mendalam dengan Tensorflow atau Pytorch?
Mar 10, 2025 pm 06:52 PM
Artikel ini membandingkan tensorflow dan pytorch untuk pembelajaran mendalam. Ia memperincikan langkah -langkah yang terlibat: penyediaan data, bangunan model, latihan, penilaian, dan penempatan. Perbezaan utama antara rangka kerja, terutamanya mengenai grap pengiraan
