 hujung hadapan web
hujung hadapan web
 tutorial js
tutorial js
 Penjelasan terperinci tentang pokok binari struktur data JavaScript dan algoritma_Pengetahuan asas
Penjelasan terperinci tentang pokok binari struktur data JavaScript dan algoritma_Pengetahuan asas
Penjelasan terperinci tentang pokok binari struktur data JavaScript dan algoritma_Pengetahuan asas
Konsep pokok binari
Pokok Binari ialah set terhingga bagi n (n>=0) nod Set itu sama ada set kosong (pokok binari kosong), atau ia terdiri daripada nod akar dan dua pokok yang saling bercabang terdiri daripada subpokok kiri dan subpokok kanan nod akar.

Ciri-ciri pokok binari
Setiap nod mempunyai paling banyak dua subpohon, jadi tiada nod dengan darjah lebih besar daripada 2 dalam pepohon binari. Setiap nod dalam pepohon binari ialah objek, dan setiap nod data mempunyai tiga penunjuk, iaitu penunjuk kepada induk, anak kiri dan anak kanan. Setiap nod disambungkan antara satu sama lain melalui penunjuk. Hubungan antara penunjuk yang disambungkan ialah hubungan ibu bapa-anak.
Takrifan nod pokok binari
Nod pokok binari ditakrifkan seperti berikut:
struct BinaryTreeNode
{
int m_nValue;
BinaryTreeNode* m_pLeft;
BinaryTreeNode* m_pRight;
};
Lima bentuk asas pokok binari
Pokok binari kosong
Hanya ada satu nod akar
Nod akar hanya mempunyai subpokok kiri
Nod akar hanya mempunyai subpokok kanan
Nod akar mempunyai kedua-dua subpokok kiri dan kanan

Hanya terdapat dua situasi untuk pokok biasa dengan tiga nod: dua lapisan atau tiga lapisan. Tetapi kerana pokok binari perlu membezakan kiri dan kanan, ia akan berkembang menjadi lima bentuk berikut:

Pokok Binari Khas
Pokok Condong
Seperti yang ditunjukkan dalam gambar ke-2 dan ke-3 dalam gambar terakhir di atas.
Pokok Binari Penuh
Dalam pokok binari, jika semua nod cawangan meninggalkan subpokok dan subpokok kanan, dan semua daun berada pada tahap yang sama, pokok binari sedemikian dipanggil pokok binari penuh. Seperti yang ditunjukkan di bawah:
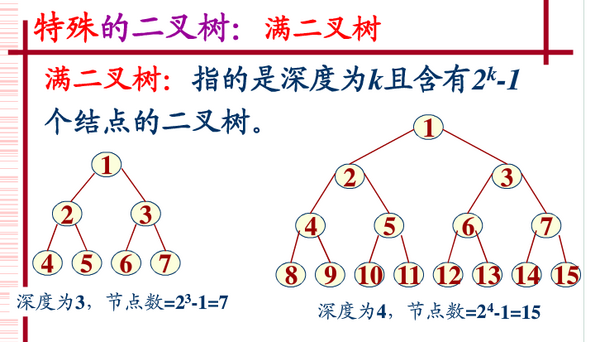
Pokok Binari Lengkap
Pokok binari yang lengkap bermakna bahagian kiri tahap terakhir penuh, bahagian kanan mungkin penuh atau tidak, dan kemudian tahap selebihnya penuh. Pokok binari dengan kedalaman k dan bilangan nod 2^k - 1 ialah pokok binari penuh (pokok binari lengkap). Ia adalah pokok dengan kedalaman k dan tiada celah.
Ciri-ciri pokok binari yang lengkap ialah:
Nod daun hanya boleh muncul pada dua peringkat bawah.
Daun yang paling rendah mesti tertumpu pada kedudukan berterusan kiri.
Pada lapisan kedua terakhir, jika terdapat nod daun, ia mesti berada dalam kedudukan berterusan di sebelah kanan.
Jika darjah nod ialah 1, maka nod itu hanya meninggalkan anak.
Pokok binari dengan pokok nod yang sama, pokok binari lengkap mempunyai kedalaman terkecil.
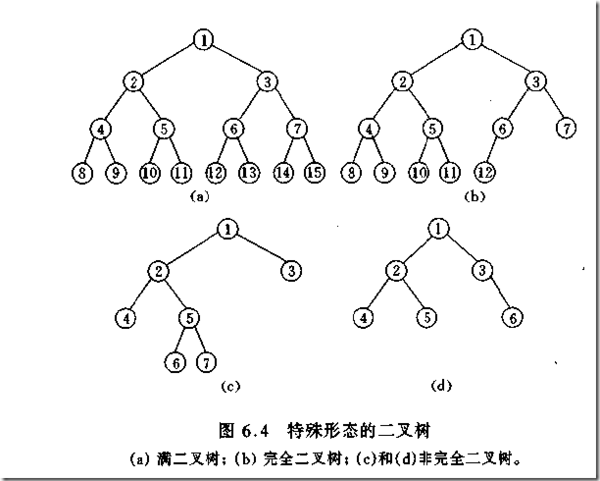
Nota: Pokok binari penuh mestilah pokok binari lengkap, tetapi pokok binari lengkap tidak semestinya pokok binari penuh.
Algoritma adalah seperti berikut:
bool is_complete(pokok *akar)
{
beratur q;
pokok *ptr;
// Lakukan lintasan pertama keluasan (laluan tahap) dan letakkan nod NULL ke dalam baris gilir
q.push(root); Manakala ((ptr = q.pop()) != NULL)
{
q.tolak(ptr->kiri);
q.push(ptr->kanan);
}
// Tentukan sama ada terdapat sebarang nod yang belum dilawati
Manakala (!q.is_empty())
{
ptr = q.pop();
// Jika terdapat nod bukan NULL yang tidak dilawati, pokok itu mempunyai lubang dan merupakan pokok binari yang tidak lengkap
pulangan palsu;
}
kembali benar;
}
Sifat pokok binari
Sifat 1 pokok binari: Terdapat paling banyak 2^(i-1) nod (i>=1) pada aras ke-i pokok binari
Sifat 2 pokok binari: Pokok binari dengan kedalaman k mempunyai paling banyak 2^k-1 nod (k>=1)
Struktur penyimpanan berjujukan pokok binari
Struktur storan berurutan bagi pokok binari menggunakan tatasusunan satu dimensi untuk menyimpan setiap nod dalam pokok binari, dan lokasi penyimpanan nod boleh mencerminkan hubungan logik antara nod.

Senarai terpaut binari
Memandangkan kebolehgunaan storan berjujukan tidak kukuh, kita mesti mempertimbangkan struktur storan rantai. Mengikut amalan antarabangsa, penyimpanan pokok binari secara amnya menggunakan struktur simpanan rantai.
Setiap nod pokok binari mempunyai paling banyak dua anak, jadi adalah idea semula jadi untuk mereka bentuk medan data dan dua medan penunjuk untuknya. Kami memanggil senarai terpaut tersebut sebagai senarai terpaut binari.

Pelintasan pokok binari
Melintasi pokok binari bermakna bermula dari nod akar dan melawat semua nod dalam pokok binari dalam susunan tertentu supaya setiap nod dilawati sekali dan hanya sekali.
Terdapat tiga cara untuk melintasi pokok binari, seperti berikut:
(1) Prapesan traversal (DLR), mula-mula lawati nod akar, kemudian lintasi subpokok kiri, dan akhirnya melintasi subpokok kanan. Singkatan akar-kiri-kanan.
(2) In-order traversal (LDR), mula-mula melintasi subpokok kiri, kemudian melawati nod akar, dan akhirnya melintasi subtree kanan. Disingkatkan sebagai kiri-akar-kanan.
(3) Postorder traversal (LRD), mula-mula melintasi sub pokok kiri, kemudian melintasi subtree kanan, dan akhirnya melawat nod akar. Disingkatkan sebagai akar kiri-kanan.
Preorder traversal:
Jika pokok binari kosong, tiada operasi kembali, jika tidak, nod akar dilawati dahulu, kemudian subpokok kiri dilalui dalam prapesanan, dan kemudian subpokok kanan dilalui dalam prapesanan.
Turutan rentas ialah: A B D H I E J C F K G
//Pre-order traversal
fungsi prapesanan(nod){
Jika(!nod == null){
putstr(node.show() " ");
prapesan(nod.kiri);
prapesan(node.kanan);
}
}
Perjalanan mengikut urutan:
Jika pepohon kosong, tiada operasi kembali, jika tidak bermula dari nod akar (perhatikan bahawa nod akar tidak dilawati dahulu), lalui subpokok kiri nod akar mengikut tertib, kemudian lawati nod akar, dan akhirnya Traverse subtree kanan mengikut tertib.

Turutan rentas ialah: H D I B E J A F K C G
//Gunakan rekursi untuk melaksanakan traversal tertib
fungsi inOrder(nod){
Jika(!(nod == null)){
inOrder(node.left);//Lawati subpokok kiri dahulu
putstr(node.show() " ");//Lawati nod akar sekali lagi
inOrder(node.right);//Akses terakhir ke subpokok kanan
}
}
Perjalanan pasca pesanan:
Jika pokok itu kosong, operasi tanpa operasi kembali jika tidak, subpokok kiri dan kanan dilalui dari kiri ke kanan, mula-mula daun dan kemudian nod, dan akhirnya nod akar dilawati.

Turutan rentas ialah: H I D J E B K F G C A
//Perjalanan pasca pesanan
fungsi postOrder(nod){
Jika(!nod == null){
PostOrder(node.left);
postOrder(node.right);
putStr(node.show() " ");
}
}
Laksanakan pepohon carian binari
Pokok carian binari (BST) terdiri daripada nod, jadi kami mentakrifkan objek nod Nod seperti berikut:
fungsi Nod(data,kiri,kanan){
This.data = data;
This.left = left;//Simpan pautan nod kiri
This.right = right;
This.show = tunjukkan;
}
function show(){
Kembalikan this.data;//Paparkan data yang disimpan dalam nod
}
Cari nilai maksimum dan minimum
Mencari nilai minimum dan maksimum pada BST adalah sangat mudah, kerana nilai yang lebih kecil sentiasa pada nod anak kiri, untuk mencari nilai minimum pada BST, hanya melintasi subpokok kiri sehingga nod terakhir ditemui
Cari nilai minimum
fungsi getMin(){
var current = this.root;
While(!(current.left == null)){
Semasa = semasa.kiri;
}
Kembalikan data semasa;
}
Kaedah ini merentasi subpokok kiri BST satu demi satu sehingga ia melintasi ke nod paling kiri BST, yang ditakrifkan sebagai:
current.left = null;
Pada masa ini, nilai yang disimpan pada nod semasa ialah nilai minimum
Cari nilai maksimum
Mencari nilai maksimum pada BST hanya memerlukan merentasi subpokok kanan sehingga nod terakhir ditemui, dan nilai yang disimpan pada nod ini ialah nilai maksimum.
fungsi getMax(){
var current = this.root;
Manakala(!(semasa.kanan == null)){
semasa = semasa.kanan;
}
Kembalikan data semasa;
}

Alat AI Hot

Undresser.AI Undress
Apl berkuasa AI untuk mencipta foto bogel yang realistik

AI Clothes Remover
Alat AI dalam talian untuk mengeluarkan pakaian daripada foto.

Undress AI Tool
Gambar buka pakaian secara percuma

Clothoff.io
Penyingkiran pakaian AI

AI Hentai Generator
Menjana ai hentai secara percuma.

Artikel Panas

Alat panas

Notepad++7.3.1
Editor kod yang mudah digunakan dan percuma

SublimeText3 versi Cina
Versi Cina, sangat mudah digunakan

Hantar Studio 13.0.1
Persekitaran pembangunan bersepadu PHP yang berkuasa

Dreamweaver CS6
Alat pembangunan web visual

SublimeText3 versi Mac
Perisian penyuntingan kod peringkat Tuhan (SublimeText3)

Topik panas
 1377
1377
 52
52
 Melaksanakan Algoritma Pembelajaran Mesin dalam C++: Cabaran dan Penyelesaian Biasa
Jun 03, 2024 pm 01:25 PM
Melaksanakan Algoritma Pembelajaran Mesin dalam C++: Cabaran dan Penyelesaian Biasa
Jun 03, 2024 pm 01:25 PM
Cabaran biasa yang dihadapi oleh algoritma pembelajaran mesin dalam C++ termasuk pengurusan memori, multi-threading, pengoptimuman prestasi dan kebolehselenggaraan. Penyelesaian termasuk menggunakan penunjuk pintar, perpustakaan benang moden, arahan SIMD dan perpustakaan pihak ketiga, serta mengikuti garis panduan gaya pengekodan dan menggunakan alat automasi. Kes praktikal menunjukkan cara menggunakan perpustakaan Eigen untuk melaksanakan algoritma regresi linear, mengurus memori dengan berkesan dan menggunakan operasi matriks berprestasi tinggi.
 Terokai prinsip asas dan pemilihan algoritma bagi fungsi isihan C++
Apr 02, 2024 pm 05:36 PM
Terokai prinsip asas dan pemilihan algoritma bagi fungsi isihan C++
Apr 02, 2024 pm 05:36 PM
Lapisan bawah fungsi C++ sort menggunakan isihan gabungan, kerumitannya ialah O(nlogn), dan menyediakan pilihan algoritma pengisihan yang berbeza, termasuk isihan pantas, isihan timbunan dan isihan stabil.
 Bandingkan struktur data kompleks menggunakan perbandingan fungsi Java
Apr 19, 2024 pm 10:24 PM
Bandingkan struktur data kompleks menggunakan perbandingan fungsi Java
Apr 19, 2024 pm 10:24 PM
Apabila menggunakan struktur data kompleks dalam Java, Comparator digunakan untuk menyediakan mekanisme perbandingan yang fleksibel. Langkah-langkah khusus termasuk: mentakrifkan kelas pembanding, menulis semula kaedah bandingkan untuk menentukan logik perbandingan. Buat contoh pembanding. Gunakan kaedah Collections.sort, menghantar contoh koleksi dan pembanding.
 Algoritma pengesanan yang dipertingkatkan: untuk pengesanan sasaran dalam imej penderiaan jauh optik resolusi tinggi
Jun 06, 2024 pm 12:33 PM
Algoritma pengesanan yang dipertingkatkan: untuk pengesanan sasaran dalam imej penderiaan jauh optik resolusi tinggi
Jun 06, 2024 pm 12:33 PM
01Garis prospek Pada masa ini, sukar untuk mencapai keseimbangan yang sesuai antara kecekapan pengesanan dan hasil pengesanan. Kami telah membangunkan algoritma YOLOv5 yang dipertingkatkan untuk pengesanan sasaran dalam imej penderiaan jauh optik resolusi tinggi, menggunakan piramid ciri berbilang lapisan, strategi kepala pengesanan berbilang dan modul perhatian hibrid untuk meningkatkan kesan rangkaian pengesanan sasaran dalam imej penderiaan jauh optik. Menurut set data SIMD, peta algoritma baharu adalah 2.2% lebih baik daripada YOLOv5 dan 8.48% lebih baik daripada YOLOX, mencapai keseimbangan yang lebih baik antara hasil pengesanan dan kelajuan. 02 Latar Belakang & Motivasi Dengan perkembangan pesat teknologi penderiaan jauh, imej penderiaan jauh optik resolusi tinggi telah digunakan untuk menggambarkan banyak objek di permukaan bumi, termasuk pesawat, kereta, bangunan, dll. Pengesanan objek dalam tafsiran imej penderiaan jauh
 Aplikasi algoritma dalam pembinaan 58 platform potret
May 09, 2024 am 09:01 AM
Aplikasi algoritma dalam pembinaan 58 platform potret
May 09, 2024 am 09:01 AM
1. Latar Belakang Pembinaan 58 Portrait Platform Pertama sekali, saya ingin berkongsi dengan anda latar belakang pembinaan 58 Portrait Platform. 1. Pemikiran tradisional platform pemprofilan tradisional tidak lagi mencukupi Membina platform pemprofilan pengguna bergantung pada keupayaan pemodelan gudang data untuk menyepadukan data daripada pelbagai barisan perniagaan untuk membina potret pengguna yang tepat untuk memahami tingkah laku, minat pengguna dan keperluan, dan menyediakan keupayaan sampingan, akhirnya, ia juga perlu mempunyai keupayaan platform data untuk menyimpan, bertanya dan berkongsi data profil pengguna dan menyediakan perkhidmatan profil dengan cekap. Perbezaan utama antara platform pemprofilan perniagaan binaan sendiri dan platform pemprofilan pejabat pertengahan ialah platform pemprofilan binaan sendiri menyediakan satu barisan perniagaan dan boleh disesuaikan atas permintaan platform pertengahan pejabat berkhidmat berbilang barisan perniagaan, mempunyai kompleks pemodelan, dan menyediakan lebih banyak keupayaan umum. 2.58 Potret pengguna latar belakang pembinaan potret di platform tengah 58
 Struktur dan algoritma data Java: penjelasan mendalam
May 08, 2024 pm 10:12 PM
Struktur dan algoritma data Java: penjelasan mendalam
May 08, 2024 pm 10:12 PM
Struktur data dan algoritma ialah asas pembangunan Java Artikel ini meneroka secara mendalam struktur data utama (seperti tatasusunan, senarai terpaut, pepohon, dll.) dan algoritma (seperti pengisihan, carian, algoritma graf, dll.) dalam Java. Struktur ini diilustrasikan dengan contoh praktikal, termasuk menggunakan tatasusunan untuk menyimpan skor, senarai terpaut untuk mengurus senarai beli-belah, tindanan untuk melaksanakan rekursi, baris gilir untuk menyegerakkan benang, dan pepohon dan jadual cincang untuk carian dan pengesahan pantas. Memahami konsep ini membolehkan anda menulis kod Java yang cekap dan boleh diselenggara.
 Struktur data PHP: Keseimbangan pepohon AVL, mengekalkan struktur data yang cekap dan teratur
Jun 03, 2024 am 09:58 AM
Struktur data PHP: Keseimbangan pepohon AVL, mengekalkan struktur data yang cekap dan teratur
Jun 03, 2024 am 09:58 AM
Pokok AVL ialah pokok carian binari seimbang yang memastikan operasi data yang pantas dan cekap. Untuk mencapai keseimbangan, ia melakukan operasi belok kiri dan kanan, melaraskan subpokok yang melanggar keseimbangan. Pokok AVL menggunakan pengimbangan ketinggian untuk memastikan ketinggian pokok sentiasa kecil berbanding bilangan nod, dengan itu mencapai kerumitan masa logaritma (O(logn)) operasi carian dan mengekalkan kecekapan struktur data walaupun pada set data yang besar.
 Algoritma CVM terobosan menyelesaikan lebih daripada 40 tahun masalah pengiraan! Saintis komputer membelek syiling untuk mengetahui perkataan unik untuk 'Hamlet'
Jun 07, 2024 pm 03:44 PM
Algoritma CVM terobosan menyelesaikan lebih daripada 40 tahun masalah pengiraan! Saintis komputer membelek syiling untuk mengetahui perkataan unik untuk 'Hamlet'
Jun 07, 2024 pm 03:44 PM
Mengira kedengaran mudah, tetapi sangat sukar untuk dilaksanakan dalam amalan. Bayangkan anda diangkut ke hutan hujan tropika yang asli untuk menjalankan banci hidupan liar. Setiap kali anda melihat haiwan, ambil gambar. Kamera digital hanya merekodkan jumlah bilangan haiwan yang dijejaki, tetapi anda berminat dengan bilangan haiwan unik, tetapi tiada statistik. Jadi apakah cara terbaik untuk mengakses populasi haiwan yang unik ini? Pada ketika ini, anda mesti berkata, mula mengira sekarang dan akhirnya bandingkan setiap spesies baharu daripada foto ke senarai. Walau bagaimanapun, kaedah pengiraan biasa ini kadangkala tidak sesuai untuk jumlah maklumat sehingga berbilion-bilion penyertaan. Para saintis komputer dari Institut Statistik India, UNL, dan Universiti Nasional Singapura telah mencadangkan algoritma baharu - CVM. Ia boleh menganggarkan pengiraan item yang berbeza dalam senarai panjang.



