Jumlah kandungan berkaitan 10000
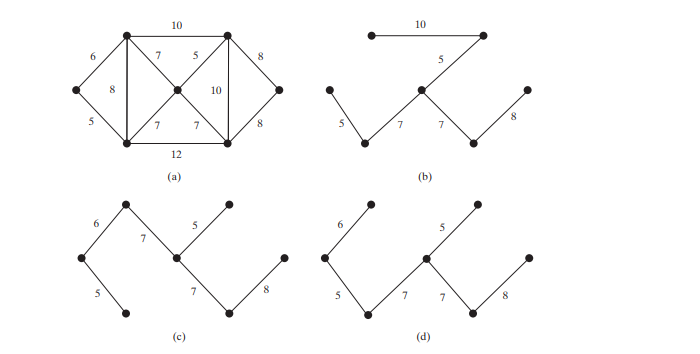
Pokok Rentang Minimum
Pengenalan Artikel:Pokok rentang minimum graf ialah pokok rentang dengan jumlah pemberat minimum.
Sesuatu graf mungkin mempunyai banyak pokok rentang. Katakan bahawa tepi ditimbang. Pokok rentang minimum mempunyai jumlah berat minimum. Contohnya, pokok dalam Rajah
2024-09-06
komen 0
1192

Bagaimana untuk menulis algoritma pokok rentang minimum menggunakan C#
Pengenalan Artikel:Cara menggunakan C# untuk menulis algoritma pepohon rentang minimum Algoritma pepohon rentang minimum ialah algoritma teori graf yang penting, yang digunakan untuk menyelesaikan masalah ketersambungan graf. Dalam sains komputer, pokok rentang minimum merujuk kepada pokok rentang bagi graf bersambung di mana jumlah pemberat semua tepi pokok rentang adalah yang terkecil. Artikel ini akan memperkenalkan cara menggunakan C# untuk menulis algoritma pepohon rentang minimum dan memberikan contoh kod khusus. Pertama, kita perlu mentakrifkan struktur data graf untuk mewakili masalah. Dalam C#, anda boleh menggunakan matriks bersebelahan untuk mewakili graf. Matriks bersebelahan ialah tatasusunan dua dimensi di mana setiap elemen mewakili
2023-09-19
komen 0
731

Algoritma Pokok Spanning Minimum Kruskal - Algoritma Tamak dalam C++
Pengenalan Artikel:Pokok rentang ialah subgraf bagi graf tidak terarah yang menghubungkan semua bucu. Terdapat banyak pokok rentang dalam graf. Pokok rentang minimum (MST) pada setiap graf mempunyai berat yang sama atau lebih kecil daripada semua pokok rentang yang lain. Pemberat diberikan pada tepi pokok rentang, dan jumlahnya ialah berat yang diberikan kepada setiap tepi. Oleh kerana V ialah bilangan bucu dalam graf, bilangan tepi pokok rentang minimum ialah (V-1), dengan V ialah bilangan tepi. Gunakan algoritma Kruskal untuk mencari pokok rentang minimum Semua tepi hendaklah disusun dalam susunan tidak menurun mengikut berat. Pilih bahagian yang paling kecil. Jika tiada gelung terbentuk, tepi disertakan. Langkah 2 hendaklah dilakukan sehingga pokok rentang mempunyai (V-1) tepi. Dalam hal ini, kita disuruh menggunakan pendekatan tamak. Pilihan tamak adalah memilih kelebihan dengan berat terkecil. Contohnya: pokok rentang minimum graf ini ialah (9-1)=8
2023-08-28
komen 0
1218

Bagaimana untuk melaksanakan algoritma pokok rentang minimum menggunakan java
Pengenalan Artikel:Cara menggunakan Java untuk melaksanakan algoritma pepohon rentang minimum Algoritma pepohon rentang minimum ialah masalah klasik dalam teori graf, yang digunakan untuk menyelesaikan pepohon rentang minimum bagi graf berwajaran. Artikel ini akan memperkenalkan cara menggunakan bahasa Java untuk melaksanakan algoritma ini dan memberikan contoh kod khusus. Huraian Masalah Memandangkan graf bersambung G, di mana setiap tepi mempunyai pemberat, ia dikehendaki mencari pokok rentang minimum T supaya jumlah pemberat semua tepi dalam T adalah minimum. Algoritma Prim Algoritma Prim ialah algoritma tamak yang digunakan untuk menyelesaikan masalah pokok rentang minimum. idea asasnya
2023-09-21
komen 0
1108

Cara menggunakan algoritma pokok rentang minimum dalam C++
Pengenalan Artikel:Cara menggunakan algoritma pepohon rentang minimum dalam C++ Minimum Spanning Tree (MST) ialah konsep penting dalam teori graf Ia mewakili subset tepi yang menghubungkan semua bucu graf tidak berarah dan berat tepi ini adalah dan min. Terdapat banyak algoritma yang boleh digunakan untuk menyelesaikan pokok rentang minimum, seperti algoritma Prim dan algoritma Kruskal. Artikel ini akan memperkenalkan cara menggunakan C++ untuk melaksanakan algoritma Prim dan algoritma Kruskal, dan memberikan contoh kod khusus. Algoritma Prim ialah a
2023-09-20
komen 0
1269

Bagaimana untuk melaksanakan algoritma pepohon rentang minimum graf menggunakan java
Pengenalan Artikel:Cara menggunakan Java untuk melaksanakan algoritma pokok rentang minimum untuk graf Pengenalan konsep: Pokok Rentang Minimum (MST) merujuk kepada mencari pokok dalam graf berwajaran terarah atau graf tidak terarah supaya ia mengandungi semua bucu dalam graf dan Jumlah pemberat adalah yang terkecil. Terdapat banyak algoritma pokok rentang minimum, dua algoritma paling klasik ialah algoritma Prim dan algoritma Kruskal. Algoritma Prim: Algoritma Prim ialah algoritma tamak berasaskan titik yang bermula dari puncak dan kemudian berkembang secara beransur-ansur
2023-09-19
komen 0
1279

Algoritma Boruvka dalam C++ untuk pokok rentang minimum
Pengenalan Artikel:Dalam teori graf, mencari pokok rentang minimum (MST) bagi graf berwajaran bersambung adalah masalah biasa. MST ialah subset tepi graf yang menghubungkan semua bucu dan meminimumkan jumlah berat tepi. Algoritma yang cekap untuk menyelesaikan masalah ini ialah algoritma Boruvka. Syntax structEdge{intsrc,dest,weight;};//Definethestructuretorepresentasubsetforunion-findstructSubset{intparent,rank;};Algoritma Sekarang, mari kita gariskan langkah-langkah yang terlibat dalam mencari pokok rentang minimum dalam algoritma Boruvka − Mulakan MST sebagai set kosong . untuk setiap bucu
2023-08-27
komen 0
876

Bagaimana untuk menyelesaikan masalah pokok rentang minimum dalam PHP menggunakan kaedah divide-and-conquer dan mendapatkan penyelesaian yang optimum?
Pengenalan Artikel:Bagaimana untuk menyelesaikan masalah pokok rentang minimum dalam PHP menggunakan kaedah bahagi-dan-takluk dan dapatkan penyelesaian yang optimum? Pohon rentang minimum ialah masalah klasik dalam teori graf, yang bertujuan untuk mencari subset semua bucu dalam graf yang disambungkan, dan menyambungkan tepi supaya subset membentuk pokok, dan jumlah pemberat semua tepi adalah yang terkecil. Kaedah divide-and-conquer ialah idea untuk menguraikan masalah besar kepada beberapa sub-masalah, kemudian menyelesaikan sub-masalah satu demi satu dan akhirnya menggabungkan hasilnya. Menggunakan kaedah divide-and-conquer untuk menyelesaikan masalah pokok rentang minimum dalam PHP boleh dicapai dengan mengikuti langkah-langkah berikut. Tentukan struktur data graf:
2023-09-19
komen 0
919

Bagaimana untuk menggunakan algoritma tamak untuk mencapai penyelesaian optimum masalah pokok rentang minimum dalam PHP?
Pengenalan Artikel:Bagaimana untuk menggunakan algoritma tamak untuk mencapai penyelesaian optimum masalah pokok rentang minimum dalam PHP? Masalah pokok rentang minimum (MinimumSpanningTree) adalah untuk mencari subpokok dalam graf tidak bersambung yang bersambung supaya subpokok ini mengandungi semua bucu dalam graf dan jumlah pemberat semua tepi adalah yang terkecil. Algoritma tamak adalah salah satu kaedah biasa untuk menyelesaikan masalah ini secara beransur-ansur mencari penyelesaian optimum global dengan memilih penyelesaian optimum semasa setiap kali. Pertama, kita perlu menentukan kelas graf untuk menyimpan struktur graf dan berat tepi. Berikut adalah contoh
2023-09-19
komen 0
1032

Mengapakah algoritma pokok rentang minimum Prim dan Kruskal gagal dalam graf terarah?
Pengenalan Artikel:Kaedah Prim dan algoritma Kruskal ialah dua kaedah biasa untuk mencari MST (pokok rentang minimum) dalam graf tidak terarah. Walau bagaimanapun, teknik ini tidak boleh menjana MST yang betul untuk graf terarah. Ini kerana graf terarah tidak sesuai dengan andaian asas dan kaedah yang digunakan oleh algoritma Prim dan Kruskal. Algoritma Prim Pertama, terdapat algoritma Prim, yang melibatkan penambahan tepi pada pokok rentang minimum yang mengembang dengan cara yang tamak sehingga semua bucu ditutup. Bucu di dalam MST disambungkan ke bucu di luar MST melalui tepi dengan berat terendah. Memandangkan semua tepi dalam graf tidak terarah boleh bergerak ke mana-mana arah, laluan terpendek dari MST ke bucu luaran mudah dicari. Walau bagaimanapun, dalam graf terarah, tepi sentiasa menghala ke satu arah dan mungkin tiada garis lurus
2023-09-02
komen 0
665
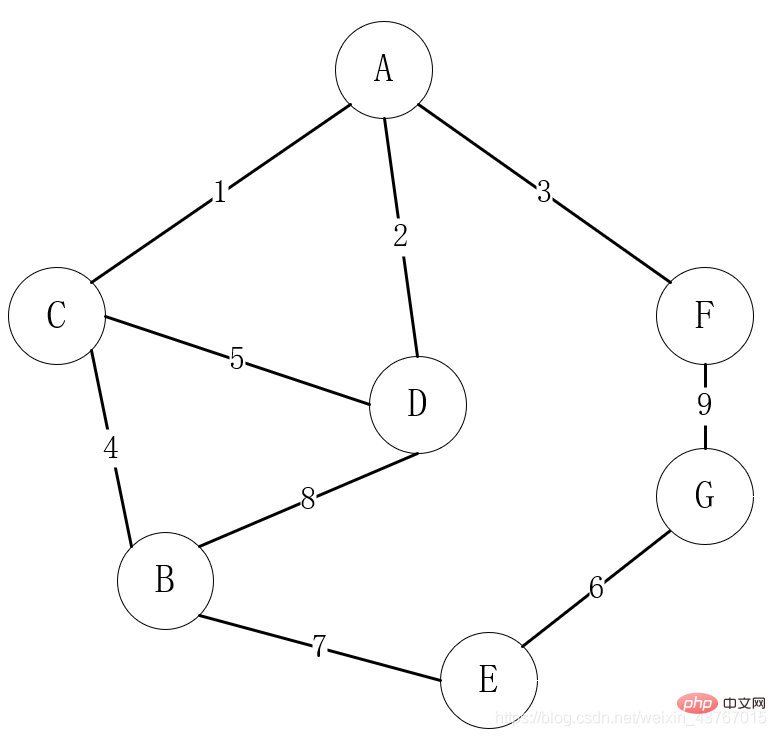
Bagaimana untuk mencari pokok rentang minimum di Jawa
Pengenalan Artikel:1 Gambaran Keseluruhan Pokok Spanning Tree Spanning Minimum (SpanningTree): Pokok spanning graf bersambung merujuk kepada subgraf bersambung, yang mengandungi semua n bucu dalam graf, tetapi hanya n-1 tepi yang cukup untuk membentuk pokok. Sebatang pokok rentang dengan n bucu hanya mempunyai n-1 tepi Jika satu lagi tepi ditambah pada pokok rentang, ia pasti akan membentuk kitaran. Pokok Rentang Minimum (MinimumSpanningTree): Di antara semua pokok rentang dalam graf bersambung, berat semua tepi dan pokok rentang terkecil dipanggil pokok rentang minimum. Dalam kehidupan, struktur grafik adalah yang paling banyak digunakan. Sebagai contoh, dalam pemilihan laluan pembinaan rangkaian komunikasi biasa, kampung boleh dianggap sebagai bucu Jika terdapat laluan komunikasi antara kampung, ia dikira sebagai tepi atau lengkok antara dua titik.
2023-04-29
komen 0
727

Penjelasan terperinci tentang algoritma pokok rentang minimum dalam PHP
Pengenalan Artikel:Penjelasan terperinci tentang algoritma pokok rentang minimum dalam PHP Minimum Spanning Tree (pendek kata MST) adalah konsep penting dalam teori graf, yang digunakan untuk menyelesaikan masalah memilih tepi berat minimum graf yang disambungkan. Dalam bahasa PHP, kita boleh mencapai fungsi ini melalui beberapa algoritma pokok rentang minimum klasik. Artikel ini akan memperkenalkan secara terperinci dua algoritma pokok rentang minimum yang biasa digunakan: algoritma Prim dan algoritma Kruskal, dan memberikan contoh kod PHP yang sepadan. 1. Algoritma prim Algoritma prim ialah a
2023-07-07
komen 0
1302

关于最小生成树的实例详解
Pengenalan Artikel:文章转载自:最小生成树-Prim算法和Kruskal算法
图的生成树是它的一棵含有所有顶点的无环连通子图,一棵加权图的最小生成树是它的一棵权值最小的生成树。
Prim算法
算法简单描述
1).输入:一个加权连通图,其中顶点集合为V,边集合为E;
2).初始化:Vnew = {x},其中x为集合V中的任一节点(起始点),Enew = {},为空;
3).重复下列操作,直到Vnew
2017-06-25
komen 0
3467

Soal berat minimum dalam subpokok bermula dari nod X dan jarak paling banyak D
Pengenalan Artikel:Apabila melakukan pengaturcaraan komputer, kadangkala adalah perlu untuk mencari berat minimum subpokok yang berasal dari nod tertentu, dengan syarat subpokok tidak boleh mengandungi nod yang lebih daripada unit D dari nod yang ditentukan. Masalah ini timbul dalam pelbagai bidang dan aplikasi, termasuk teori graf, algoritma berasaskan pokok, dan pengoptimuman rangkaian. Subpokok ialah subset struktur pokok yang lebih besar, dengan nod yang ditentukan berfungsi sebagai nod akar subpokok. Subpohon mengandungi semua keturunan nod akar dan tepi penghubungnya. Berat nod merujuk kepada nilai khusus yang diberikan kepada nod itu, yang boleh mewakili kepentingan, kepentingan atau metrik lain yang berkaitan. Dalam masalah ini, matlamatnya adalah untuk mencari berat minimum antara semua nod dalam subpokok sambil mengehadkan subpokok kepada nod yang paling banyak unit D dari nod akar. Dalam artikel berikut, kita akan menyelidiki kerumitan perlombongan pemberat minimum daripada subpokok
2023-08-25
komen 0
1471

Proses penjanaan pepohon keputusan adalah berkaitan dengan algoritma id3
Pengenalan Artikel:Algoritma ID3 ialah algoritma klasik untuk menghasilkan pepohon keputusan, yang dicadangkan oleh Ross Quinlan pada tahun 1986. Ia memilih ciri terbaik sebagai pemisahan nod dengan mengira keuntungan maklumat bagi setiap ciri. Algoritma ID3 digunakan secara meluas dalam bidang pembelajaran mesin dan perlombongan data, terutamanya memainkan peranan penting dalam tugas klasifikasi. Penggunaannya boleh meningkatkan ketepatan model dan kebolehtafsiran sambil juga dapat mengendalikan set data yang kompleks dengan pelbagai ciri dan kategori. Pokok keputusan ialah struktur pokok yang digunakan untuk pengelasan atau regresi. Ia terdiri daripada nod dan tepi Nod mewakili ciri atau atribut, dan tepi mewakili nilai atau keputusan yang mungkin. Nod akar mewakili ciri yang paling penting, dan nod daun mewakili hasil pengelasan akhir. Pohon keputusan menentukan hasil pengelasan dengan menilai secara beransur-ansur nilai ciri setiap kali
2024-01-22
komen 0
1146
PHP树的深度编历生成迷宫及A*自动寻路算法实例分析
Pengenalan Artikel:PHP树的深度编历生成迷宫及A*自动寻路算法实例分析。PHP树的深度编历生成迷宫及A*自动寻路算法实例分析 这篇文章主要介绍了PHP树的深度编历生成迷宫及A*自动寻路算法,实例分析了php实现A*寻
2016-06-13
komen 0
1082












