Jumlah kandungan berkaitan 10000

Tutorial yang ringkas dan mudah difahami untuk menyelesaikan pembahagi sepunya terbesar dalam bahasa C
Pengenalan Artikel:Tutorial mudah dan mudah difahami tentang menyelesaikan pembahagi sepunya terbesar dalam bahasa C 1. Pengenalan Dalam matematik, pembahagi sepunya terbesar (Pembahagi Sepunya Terbesar, singkatannya GCD) merujuk kepada integer positif terbesar yang boleh membahagi dua atau lebih integer. Mencari pembahagi sepunya terbesar adalah sangat biasa dalam pengaturcaraan dan boleh digunakan untuk memudahkan pecahan, perkadaran dan operasi integer. Artikel ini akan memperkenalkan cara menggunakan bahasa C untuk menulis program penyelesaian pembahagi biasa yang paling mudah, termasuk contoh kod khusus. 2. Analisis Algoritma Tutorial ini akan menggunakan kaedah pembahagian euclidean untuk menyelesaikan maksimum
2024-02-20
komen 0
801

Python实现求解最大公约数的方法
Pengenalan Artikel:这次给大家带来Python实现求解最大公约数的方法,Python实现求解最大公约数的注意事项有哪些,下面就是实战案例,一起来看一下。
2018-04-09
komen 0
5981

Penyelidikan tentang algoritma untuk mencari pembahagi sepunya terbesar dalam bahasa C
Pengenalan Artikel:Pengenalan kepada algoritma untuk mencari pembahagi sepunya terbesar dalam bahasa C: Pembahagi sepunya terbesar (Pembahagi Sepunya Terhebat, singkatannya GCD) ialah konsep biasa dalam matematik, yang merujuk kepada pembahagi sepunya terbesar bagi dua atau lebih integer. Dalam sains komputer, mencari pembahagi sepunya terbesar adalah keperluan biasa. Artikel ini akan meneroka beberapa algoritma untuk mencari pembahagi sepunya terbesar dalam bahasa C dan memberikan contoh kod khusus. 1. Algoritma Euclidean (kaedah pembahagian euclidean): Algoritma Euclidean ialah algoritma kuno dan mudah yang berulang kali membahagi dua
2024-02-22
komen 0
649

Pembelajaran Gelung PHP 9: Dapatkan faktor sepunya terbesar antara dua nombor yang diberi
Pengenalan Artikel:Dalam artikel sebelumnya "Pembelajaran Tatasusunan PHP: Mengembalikan Semua Faktor Sepunya dan Faktor Sepunya Terbesar antara Dua Nombor Diberi", kami memperkenalkan kaedah untuk mendapatkan semua faktor sepunya dua integer dan mencari pembahagi sepunya terbesar. Kali ini kami akan memperkenalkan kepada anda kaedah mencari pembahagi biasa yang paling hebat. Rakan-rakan yang berminat boleh mempelajarinya~
2021-08-13
komen 0
3736

Bagaimana untuk mengira GCD dua atau lebih nombor/tatasusunan dalam JavaScript?
Pengenalan Artikel:Pembahagi sepunya terbesar (GCD) bagi dua atau lebih nombor, juga dikenali sebagai faktor sepunya terbesar (GCF) atau faktor sepunya tertinggi (HCF), ialah integer positif terbesar yang boleh dibahagikan dengan nilai tertentu tanpa baki. Dengan kata lain, GCD ialah pembahagi terbesar dua nombor. Sebagai contoh, GCD bagi 24 dan 36 ialah 12. Bagaimana untuk mengira dua nombor? Terdapat beberapa cara berbeza untuk mengira GCD bagi dua nombor, tetapi kaedah yang paling biasa ialah algoritma Euclidean. Algoritma Euclidean ialah kaedah berulang yang bermula dengan dua nombor a dan b dan mencari GCD bagi a dan b. Idea asas algoritma Euclidean adalah untuk terus menolak nombor yang lebih kecil daripada nombor yang lebih besar sehingga dua nombor adalah sama. Sebagai contoh, mari kita cari GCD untuk mengira 24 dan 36 menggunakan algoritma Euclidean. Dibuka dari 24 dan 36
2023-09-10
komen 0
1149
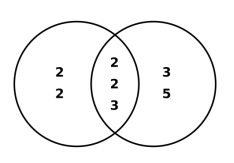
Cetak N baris nombor supaya pembahagi sepunya terbesar antara setiap pasangan nombor ialah K
Pengenalan Artikel:GCDGCD mewakili pembahagi sepunya terbesar bagi dua atau lebih integer, tidak termasuk 0. Contohnya, untuk mencari pembahagi sepunya terbesar bagi 48 dan 180 48 = 2 × 2 × 2 × 2 × 3 180 = 2 × 2 × 3 × 3 × 5 pembahagi sepunya terbesar Nombor=2×2×3=12. Dalam masalah yang diberikan, N baris harus dicetak di mana elemen mempunyai pembahagi sepunya terbesar yang ditentukan Input:N=2GCD=2Ouput:2-4-6-1014-16-18-2
2023-08-27
komen 0
1046

Penjelasan terperinci tentang cara menggunakan bahasa C untuk mencari pembahagi sepunya terbesar
Pengenalan Artikel:Penjelasan terperinci tentang kaedah mencari pembahagi sepunya terbesar dalam bahasa C Pembahagi sepunya terbesar (GCD, Pembahagi Sepunya Terhebat) ialah konsep yang biasa digunakan dalam matematik, yang merujuk kepada pembahagi terbesar di antara beberapa integer. Dalam bahasa C, kita boleh menggunakan banyak kaedah untuk mencari pembahagi sepunya yang paling hebat. Artikel ini akan memperincikan beberapa kaedah biasa ini dan memberikan contoh kod khusus. Kaedah 1: Pembahagian Euclidean ialah kaedah klasik untuk mencari pembahagi sepunya terbesar bagi dua nombor. Idea asasnya ialah membahagikan pembahagi dan baki dua nombor secara berterusan
2024-02-18
komen 0
856

Program C++ untuk mengira faktor sepunya terbesar
Pengenalan Artikel:Faktor sepunya tertinggi atau pembahagi sepunya terbesar ialah faktor yang boleh membahagi dua atau lebih nilai secara serentak tanpa menghasilkan sebarang baki. Dalam artikel ini, kita akan membincangkan beberapa cara untuk melaksanakan HCF/GCD bagi dua nombor dalam C++. Ini hanyalah penyelesaian matematik, terdapat beberapa algoritma untuk mencari pembahagi sepunya terbesar. Kaedah Euclidean ialah cara biasa untuk mencari pembahagi sepunya terbesar. Kami akan menggunakan algoritma yang sama dalam mod berulang dan rekursif. Penyelesaian berulang untuk mencari pembahagi sepunya terbesar menggunakan kaedah lelaran Euclidean dibentangkan dalam bahagian algoritma. Algoritma mengambil sebagai input dua nombor a dan b. Jika a sama dengan 0, maka b dikembalikan. Jika b ialah 0, kembalikan a. Apabila a dan b tidak sama, lakukan operasi. Jika a>b, maka a:=a–b. Jika tidak b:
2023-09-18
komen 0
1623
Bagaimana untuk memasang sistem pengendalian win7 pada komputer
Pengenalan Artikel:Di antara sistem pengendalian komputer, sistem WIN7 adalah sistem pengendalian komputer yang sangat klasik, jadi bagaimana untuk memasang sistem win7? Editor di bawah akan memperkenalkan secara terperinci cara memasang sistem win7 pada komputer anda. 1. Mula-mula muat turun sistem Xiaoyu dan pasang semula perisian sistem pada komputer desktop anda. 2. Pilih sistem win7 dan klik "Pasang sistem ini". 3. Kemudian mula memuat turun imej sistem win7. 4. Selepas memuat turun, gunakan persekitaran, dan kemudian klik Mulakan Semula Sekarang selepas selesai. 5. Selepas memulakan semula komputer, halaman Pengurus Windows akan muncul Kami memilih yang kedua. 6. Kembali ke antara muka komputer pe untuk meneruskan pemasangan. 7. Selepas selesai, mulakan semula komputer. 8. Akhirnya datang ke desktop dan pemasangan sistem selesai. Pemasangan satu klik sistem win7
2023-07-16
komen 0
1188
php-插入排序
Pengenalan Artikel::本篇文章主要介绍了php-插入排序,对于PHP教程有兴趣的同学可以参考一下。
2016-08-08
komen 0
1044
图解找出PHP配置文件php.ini的路径的方法,_PHP教程
Pengenalan Artikel:图解找出PHP配置文件php.ini的路径的方法,。图解找出PHP配置文件php.ini的路径的方法, 近来,有不博友问php.ini存在哪个目录下?或者修改php.ini以后为何没有生效?基于以上两个问题,
2016-07-13
komen 0
786

Huawei melancarkan dua produk storan model besar AI komersial baharu, menyokong prestasi 12 juta IOPS
Pengenalan Artikel:IT House melaporkan pada 14 Julai bahawa Huawei baru-baru ini mengeluarkan "Penyimpanan tasik data pembelajaran mendalam OceanStorA310" dan "mesin FusionCubeA3000 latihan/mendorong semua-dalam-satu mesin" produk storan AI komersial baharu Pegawai berkata bahawa "dua produk ini boleh digunakan untuk latihan model AI asas." , latihan model industri dan latihan dan inferens model senario tersegmen menyediakan momentum baharu. senario tasik untuk mencapai regresi data Pengurusan data secara besar-besaran dalam keseluruhan proses AI daripada pengumpulan dan prapemprosesan kepada latihan model dan aplikasi inferens. Secara rasmi menyatakan bahawa OceanStorA310 bingkai tunggal 5U menyokong 400GB/s tertinggi industri
2023-07-16
komen 0
1522
PHP函数容器ing...
Pengenalan Artikel::本篇文章主要介绍了PHP函数容器ing...,对于PHP教程有兴趣的同学可以参考一下。
2016-08-08
komen 0
1088
PHP面向对象程序设计之接口用法,php面向对象程序设计_PHP教程
Pengenalan Artikel:PHP面向对象程序设计之接口用法,php面向对象程序设计。PHP面向对象程序设计之接口用法,php面向对象程序设计 接口是PHP面向对象程序设计中非常重要的一个概念。本文以实例形式较为详细的讲述
2016-07-13
komen 0
976
PHP面向对象程序设计之类常量用法实例,sed用法实例_PHP教程
Pengenalan Artikel:PHP面向对象程序设计之类常量用法实例,sed用法实例。PHP面向对象程序设计之类常量用法实例,sed用法实例 类常量是PHP面向对象程序设计中非常重要的一个概念,牢固掌握类常量有助于进一步提
2016-07-13
komen 0
1013

在HTML页面使用JS获取Get参数方法的示例代码分享
Pengenalan Artikel:这里是一个获取URL带QUESTRING参数的JAVASCRIPT客户端解决方案,相当于asp的request.querystring,PHP的$_GET
2017-04-24
komen 0
4123












